
Composing with the Vedic numeric table
by Manuel Rocha Iturbide
In 1989, the Mexican artist Juan Luis Díaz asked me if I could compose music with a numeric grid that he had been using for almost fifteen years to make his sculptures. I was immediately interested in this project because the relationships between numbers have always fascinated me. It is well known that many composers have used numbers to structure their music and that there has been always an interest in their beauty. The ancient Greeks attributed to the association of music and numbers a predominant place in the philosophy of the cosmos and it was perhaps Pythagoras one of the first mathematicians to study the relationship between sounds and numbers. From there on there have been different philosophers, scientists and musicians that have worked on this subject with different points of emphasis. Some researchers have studied the physical relationships between sound and numbers, for example, the theory of the generation of the overtones, which the Pythagorean School developed. On the other hand, composers have used numbers in a free and creative way to generate musical compositions.
Before presenting this numeric grid and explaining my research towards being able to compose with it, I will describe some ways that have been used in the past to do music with numbers and the reasons for which so many composers have been interested in the relationships between numbers and why have they used them to make their music.
May be one of the principal concerns thorough history about numbers is that they can make beauty out of chaos, and bring order into our minds. The school of researchers that followed Pythagoras theories taught the mathematics of music not only as a science but also as part of a philosophical moral code.
For Leonard B. Meyer music stands somewhere in between the two extremes of chance and total order. This happens in general with other artistic disciplines, the creator needs to structure his work in a coherent way, but he is also free to brake the rules and to bring the unexpected. Nonetheless, in this century we have had composers that explored the extremes as a way to brake up with tradition, and to liberate them selves from their own cultural chains. The most curious thing is that composers that went into complete chance disagreed conceptually from the ones that went into total
serialism and viceversa. I think that their music as well as their attitude towards creativity was very similar. What both were doing was to explore new musical dimensions that could not be found in the past. They really broke up completely with tradition using systems either too rational or irrational where there is little room for personal taste and emotion. The composers that went into the total ordered space chose many times numeric systems or structures to determine their music, but they used them in different ways and with different degrees of liberty. It is at the beginning of the XXth century that some composers got interested in numbers and used them freely as a tool to generate musical motives and to vary them.
One of the simplest ways to expand a musical theme and that was used very much in post-tonal music is permutation. This is the variation of the order of a series implying usually rational and not haphazard variation. Alvan Berg devised some of the first twelve-note permutations for his opera "Lulu". The following is an example of gradual permutation of a twelve note series.
(a) 1 3 5 7 9 11 2 4 6 8 10 12
(b) 1 5 9 2 6 10 3 7 11 4 8 12
(c) 1 9 6 3 11 8 5 2 10 7 4 12
(d) 1 6 11 5 10 4 9 3 8 2 7 12
(e) 1 11 10 9 8 7 6 5 4 3 12 12
(f) 1 10 8 6 4 2 11 9 7 5 3 12
(g) 1 8 4 11 7 3 10 6 2 9 5 12
(h) 1 4 7 10 2 5 8 11 3 6 9 12
(i) 1 7 2 8 3 9 etc.
Other composers have worked with numeric series to generate melodic rows or rhythm. The Italian composer Luigi Nono used the Fibonacci series in "Il canto sospeso", and Stockhausen in "Mixtur" and "Zyklus."
Another devise to generate series of notes or rhythmical values is the Pascal triangle, which has been used by Iannis Xenakis. This triangle is an infinite array and provides much information that can be used in different ways.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
The Pascal triangle
James Tenney uses the numbers of the overtone series to generate the rhythm of a piece. C for example is the fundamental and has the value of one, then comes the octave which is in the ratio of 2/1, then the twelfth (the fifth above the octave) which is 3/1, then the double octave which is 4/1 and so on. So in this case, every partial has its specific rhythm derived from its relation with the fundamental. When you have combinations of overtones like the double octave with the twelfth you have a rhythm of four against three, and when you have all the overtones going on at the same time you have a very complex rhythmical texture.

We can find another way to use numbers in John Cages early composition works when he structured whole pieces based on a number of measures having a square root so that large lengths of the piece were related to small phrases which use the same number. With this system, the structure of the whole piece is done beforehand.
It is clear that there are many different ways to relate music with numbers, we have seen how numbers can be traduced into rhythm, melody and how they can even predetermine the form of a piece.
After doing some research about the numeric system in which I am working now, I discovered that it had nothing to do with any of the methods explained before, but I found out that it was closely related to serial music, and more particularly to Integral Serialism. I will talk now about the origin of serialism and then I will present my system and compare my research with what has been done with other systems.
It was Shoenberg perhaps the first composer to structure a completely new musical system that had enough logic to be established after his death and which many composers use these days. Shoenberg moved out from the tonal system and entered the world of atonality where there are no strong points of gravity, and after working for a while in this new musical environment, he came up with a coherent system to organize his music which is called serial music. This system is any succession of the twelve tones of the chromatic scale without repetition. This row is expanded using its inversion, retrograde, and retrograde inversion. Numbers have to do with this technique because the octave in the western tempered scale is divided by twelve pitches which are a half tone apart. Thus, this scale is completely symmetrical while the diatonic scale is not symmetrical. Also, there is no strong hierarchy between pitches in the serial system while there is in tonality. Being able to number the twelve tones of the scale, it was easy to come up with different mathematical equations that tells us very fast what is the level of transposition of a given row, its inversion and its retrograde inversion.
Composers like Webern and Berg were interested in symmetry and they chose symmetrical rows for their music. In the first movement of Webern String Quartet Op. 28 he uses a row to generate his music which is arranged in retrograde symmetrical order, those limiting the 48 usual orderings of a row to only 24 (example no 1). This interest in symmetry was very strong even before the solidification of the serial system, and in the beginning of atonal music many symmetrical pitch class sets were used.

Example 1. Anton Webern series for the first movement of his string quartet Op. 28
If we number the twelve pitches of the chromatic scale from zero to eleven beginning in C, we can see how the pitch class set
0, 3, 6, 9 (diminished chord) and any of its transpositions or permutations makes it always symmetrical. It is also interesting to see that there are only three transpositions of this PCS which use different notes (1, 4, 7, 10 and 2, 5, 8, 11 being the other two). In all other transpositions this PCS maps into itself. A similar situation happens with PCS 0, 4, 8, (Augmented chord) PCS 0, 2, 4, 6, 8, 10, 12 (whole tone scale), PCS 0,1,3,4,6,7,9,11 (octatonic scale) and with the chromatic scale itself. So the most symmetrical PCS which map more times into themselves are the ones that have less variety. I bring all this up because the system that i use is a perfect symmetrical system, and many of these things will help to explain how it works.
In Serial music the twelve note series are often subdivided into small PCS which are related one to each other. Serial music is just an extension of the compositional techniques used in atonality but here the ordering of the pitches is fundamental while in atonal music the order is not so important as long as we use the same collections through all the piece. What is important in serial music is to come up with an interesting twelve-note row, and symmetry is very often a quality chosen by the composer. In example one, Webern's series can be subdivided in small dyads which are always minor seconds, and it can also be divided in two hexacords which are the same collection of notes. Adding the notes from the center to the extremes can prove the symmetry of the row. This addition is always eleven. So the two central notes of the row (C# and Bb) are the symmetrical axis. This series is very economical and you can actually divide it also in three tetrachords which are members of the same set class, so it is easy to see how important are the choices of the composer concerning the twelve note row.
Having talked enough for the moment about serial music, I will now present the numeric table I use and describe its properties.
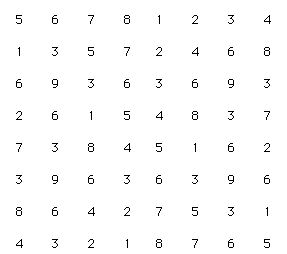
This is a numeric grid of 64 numbers which is the result of multiplying 2x1, 2x2, 2x3, 2x4, 2x5, 2x6......up to 9, then 3x1, 3x2, 3x3...... up to nine, and so on until we multiply 9x1, 9x2, 9x3, ...... until 9x9. The table is shown in example 2.
Example 2.

However, in this table, when we have a number higher than nine we reduce it by adding the two digits, so the table has only single digits as in example 3.
1 2 3 4 5 6 7 8 9
2 4 6 8 1 3 5 7 9
3 6 9 3 6 9 3 6 9
4 8 3 7 2 6 1 5 9
5 1 6 2 7 3 8 4 9
6 3 9 6 3 9 6 3 9
7 5 3 1 8 6 4 2 9
8 7 6 5 4 3 2 1 9
9 9 9 9 9 9 9 9 9
Example 3
As you can see, the outer numbers of the grid are always nine. This is because number nine is the number, which includes all the other numbers, and if you notice, the product of the addition of any line in any direction is always nine. This table was used by the Sumerians and later by the Vedic culture, and it has to do a lot with Pythagorean mathematics.
Pythagoras thought that number nine was the transcendent number and it is believed that he divided everything in cycles of nine. Number zero is the complementary of nine, so zero, nine are the same, and as nine repeats itself before the new cycle begins, it is excluded from this table. So we end up with our table of sixty-four digits which curiously is a cabalistic number and a number of great balance (example 4). Sixty four is the number of squares in the game of chess, and it's the number of the hexagrams of the
"I Ching".
The "Vedic Table" is in a way the representation of the complementary, of the "Ying" and "Yang", and it is symmetrical with itself in any direction. No wonder that it is a square, a symmetrical geometric figure (Notice in example four that the only four nines that appear in the table form a square).
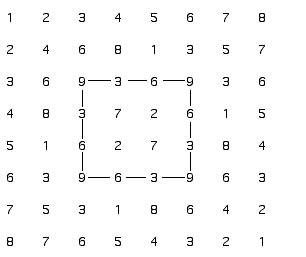
Example 4
In the Vedic table, the horizontal rows of numbers are equal to the vertical rows, and you can see how there are only four different rows of numbers because the others are the retrograde of the first. You can also see how the rows that begin with number one and number eight are complementary (the numbers add always up to nine), as well as two and seven, three and six, and four and five.
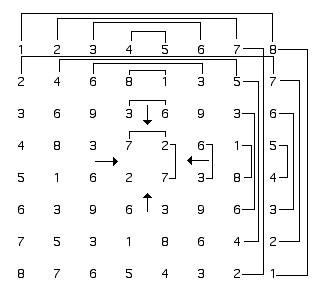
Example 5. complamentarity of numbers in the Vedic table.
It is clear now how the main characteristic of this table is complementarity of numbers that added together are nine. The Artist J.L Díaz studied these relationships and he found out that putting complementary numbers together, there were geometric figures which were the same but projected in a mirror.
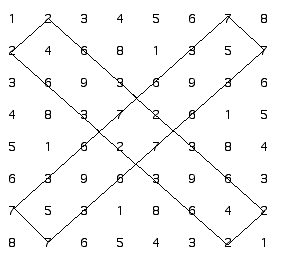
Example six. Two's and sevens.
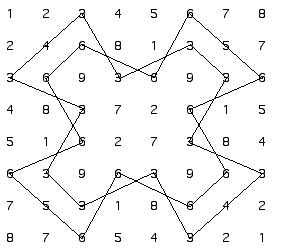
Example seven. Threes and sixes.
When Díaz asked me to do music with this grid, he was concerned about expressing the qualities of the system in the most objective way. He's approach was not to transgress the rules or laws of the system, but simply to discover its relationships and to show them through geometric designs. When he got tired of dealing with two dimensions, he had the intelligent idea of expanding this system to three dimensions by making a cube that has 512 numbers and is the result of the multiplication of the numbers in different layers. He dragged imaginary lines between the numbers in the cube and came up with three-dimensional geometric figures. The number relationships in this cube are very complex, and i am planning to work with it once i do enough research with the original table.
The problem of trying to keep with Díaz approach was that he was drawing lines between the same number, and then of its complementary number to create forms or structures which are fixed in time. How would one deal with that in music where time is the first element? I decided that the easiest way to interpret the grid was to use the numeric rows which it includes, but i thought that every time i wanted to use one of the rows, i had to use at the same time its complementary row because this is a game of dualities. Therefore, my method of traducing this system into music became something similar to the procedures used in integral serialism.
Since this is a table of eight elements, i decided to use a scale of eight notes. The logic thing would be to divide the octave in eight different tones but i did not have the proper devices to do that, and it would be difficult for instrumentalists to play with such a scale. I thought that i could use instead the octatonic scale which is a sequence of halved and whole tones (Example 8).

Example 8. Two Octatonic scales. One starts with halve tone and
the second one starts with a whole tone.
This scale does not correspond to an equal sequence of eight tones but it is a symmetrical collection. In his book "Introduction to post-tonal theory", Strauss shows an example of the four axes of symmetry in the octatonic scale (Example 9).
Example 9. For Axes of symmetry in the octatonic scale.
This scale works very well because I am dealing with symmetrical tetrachords.
I also decided to have eight different rhythmical values having an eight note as my basic unit. Therefore, I assigned a value to every number.
![]()
Now I assigned the note and rhythmic values to the rows and i did a counterpoint of two melodic lines that are always complementary between each other. This means that i start from the top and the bottom of the square so i have always two juxtaposed rows: 1 and 8, 2 and 7, 3 and 6, 4 and 5 which are the original and their retrograde version (see composition I in appendix).
There was a little difficulty interpreting the four nines in the square since i used the number eight as a unit. I decided then to assign the nines a rest of nine beats (my basic beat is one eight note). It is interesting that the two melodies have vertical coincidences when they arrive at the same time to number nine in rows 3 and 6.
I think this is a very close musical representation of the Vedic table but being so strict, there are be very few possibilities of variety, so i decided to search for new possibilities of interpreting the table.
Finding out recently that some composers in the fifties were deeply involved with integral serialism, i decided to find out about their methods so i could have more ideas. One of the compositions of this period that is quite interesting is "Structures" for two pianos written in 1952 by Pierre Boulez. This composer was a pupil of Messiaen who was one of the first European composers to write a piece with total organization in 1949.
Boulez piece is based on a twelve tone row. In Structure Ia (the first of three parts) all twelve transpositions of the series and their derived forms (inversions, retrogrades, and inverted retrogrades) are used once each in a specific order. From the original and inverted series, Boulez constructed two tables which he uses to compose many details of the music. These matrices were obtained by numbering the original series and then transposing it eleven times, starting every time in the next note (Example 10).
1 2 3 4 5 6 7 8 9 10 11 12
![]()
1 2 3 4 5 6 7 8 9 10 11 12
2 8 4 5 6 11 1 9 12 3 7 10
3 4 1 2 8 9 10 5 6 7 12 11
4 5 2 8 9 12 3 6 11 1 10 7
5 6 8 9 12 10 4 11 7 2 3 1
6 11 9 12 10 3 5 7 1 8 4 2
7 1 10 3 4 5 11 2 8 12 6 9
8 9 5 6 11 7 2 12 10 4 1 3
9 12 6 11 7 1 8 10 3 5 2 4
10 3 7 1 2 8 12 4 5 11 9 6
11 7 12 10 3 4 6 1 2 9 5 8
12 10 11 7 1 2 9 3 4 6 8 5
Example 10. Original series and 'O' matrix grid.
The matrices determine all note duration's, dynamics, and modes of attack and they are used to govern the order in which the note series are used , and to form an overall plan for note duration's. Boulez uses diagonal rows of the matrices to determine the dynamics and modes of attack. Therefore, here we have a composition based completely on the two matrices, although the overall form structure of the piece is really a free conception. In addition, number and pitch are not completely integrated. The rhythmic row has as a unit a 32nd, and the rhythmic value grows proportionally from one to twelve, but the pitches are not equally ordered from one to twelve.
This is not the place to go into a deep analysis of "Structures", and it is enough to say that even in total serialism it is difficult to be completely logical. There is always a degree of liberty that the composer assumes, and it is there where music becomes a human artistic expression. Nonetheless, i am sill interested in finding complete degrees of organization as Cage went in the opposite direction and found a complete degree of chance. In both cases, the composer looks for a way to make objective decisions and he becomes an observer of the process that he is generating.
I am now trying to use the information of the "Vedic table" in different ways to obtain variety but i am trying to respect the essence of its rules. After my research is finished, i will generate different compositions. Now i will explain the other possibilities of the table.
Besides the eight rows i worked with the first time, there are also diagonal rows, which are complementary to each other. These are as follow:

Notice how every row of each triangle is symmetrical and how they are complementary with each other (the numbers always add up to nine). From these two triangles, it is possible to make a second musical counterpoint.
I thought that i could expand this grid in order to have diversity but always keeping complementary rows. Influenced by serial theory I started to investigate about the tetrachords of the octatonic scale.
The numeric square is made out of eight tone rows with no pitch repetitions except for rows number three and six where the pitches three and six are repeated. The other rows can be divided in tetrachords and their complementary tetrachords. We can find only three different tetrachords in the table: 1 2 3 4, 2 4 6 8, and
4 8 3 7. Their complementary tetrachords are 5 6 7 8, 1 3 5 7 and 2 6 1 5 but they are only transpositions of the first.
There are a limited set of serial rows in the octatonic scale which regard the complementary principle. This is because a tetrachord cannot have two numbers, which add up to nine, if that happens then the complementary tetrachord would have the repetition of two numbers of the first tetrachord.
For example, if we make up the tetrachord 1 2 5 7 which does not exist in the Vedic table, its complementary tetrachord would be 2 4 7 8 and thus we have 2 and 7 repeated. If we have 1 3 6 2 we have the complementary tetrachord 7 3 6 8 and we have three and six repeated. I then discovered that there are only eight different possible tetrachords in the octatonic scale that goes along with their complementary tetrachords. In the numeric grid, we have only three of the eight possible tetrachords.
Here are the eight possible tetrachords and their complementary tetrachords:
Example 11. The eight possible tetrachords and
their complementary tetrachords.
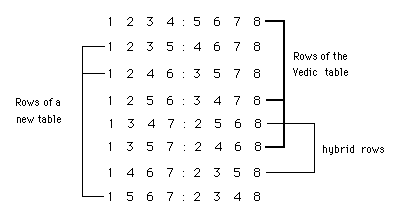
With three of the new rows, it is possible to make a new table:
1 2 6 4 5 3 7 8
2 4 3 8 1 6 5 7
6 3 9 6 3 9 6 3
4 8 6 7 2 3 1 5
5 1 3 2 7 6 8 4
3 6 9 3 6 9 3 6
7 5 6 1 8 3 4 2
8 7 3 5 4 6 2 1
Example 12. New Vedic table.
If you notice, you can generate this new table by just switching around the threes and the sixes. All the geometric figures remain the same but the tetrachords are new (except for the tetrachords of rows, three and six which are the same as in the original table).
We still have two tetrachords left. Lets use
1 7 3 4 : 5 6 2 8 to construct another table:
1 7 3 4 5 6 2 8
7 4 3 1 8 6 5 2
3 3 9 3 6 9 6 6
4 1 3 7 2 6 8 5
5 8 6 2 7 3 1 4
6 6 9 6 3 9 3 3
2 5 6 8 1 3 4 7
8 2 6 5 4 3 7 1
Example 13. Hybrid table 1.
Here i just switched the twos with the sevenths but now all the geometric figures have changed except the one with fours and fives. I would call this table a Hybrid table because it only has one tetrachord and it is complementary in different orders (with the exception of the rows at levels two and seven).
We have one more table that can be generated by the tetrachords 1 7 6 4 : 5 3 2 8.
1 7 6 4 5 3 2 8
7 4 6 1 8 3 5 2
6 6 9 6 3 9 3 3
4 1 6 7 2 3 8 5
5 8 3 2 7 6 1 4
3 3 9 3 6 9 6 6
2 5 3 8 1 6 4 7
8 2 3 5 4 6 7 1
Example 14. Hybrid table 2.
Notice how the Hybrid table two is equal to number one but with the threes and sixes switched. They also have the same geometric figures but different tetrachords.
I have expanded the original Vedic Table to four tables, thus having more information for compositional purposes.
It is also possible to use permutation with the different tables and in this way to change the order of the pitches and enrich melodic content. We can permute a whole row or only the first tetrachord
( the last step changes in automatic way the order of the complementary tetrachord ). For example, we have the row:
1 2 3 4 5 6 7 8, if we permute the row in this way:
2 3 4 5 6 7 8 1, we brake with the balance of the row
because the numbers doesn't add up to nine (from the center to the outer part). We would have to use 2 3 4 5 and find the complementary tetrachord 4 5 6 7. The problem is that in this case, we have the repetition of numbers four and five and this brakes with the serial principal of no repetition. On the other hand we could get reed off a 4 and 5 and keep only six pitches:
2 3 4 : 5 6 7. Notice how we have now a hexachord molded
by two symmetrical trichords. The only other possible hexachord in
this row is 1 2 3 : 6 7 8 and of course, the trichords can be
switched in order to have variation: 5 6 7 : 2 3 4
and 6 7 8 : 1 2 3 . This procedure can also be applied to the
tetrachords of the table, so the melodic sequence generated by
row number two, 2 4 6 8 1 3 5 7
could also be 1 3 5 7 2 4 6 8.
To have all the rows switched like this is just a matter of cutting in halve the numeric grid and changing the two blocks of place (example 13).
Example 13. Halves of Vedic table switched.
The new variation of the Vedic table shown in example 13 is not in the right order because there is no symmetry in the diagonals. The proper order of the rows is the following:
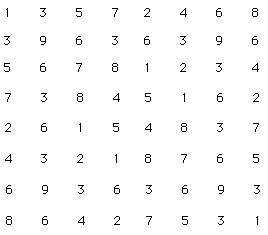
Example 14. Switched halves of Vedic table with ordered rows.
To compose with this system, should I regard the sequence of the rows in the squares or should I use them in pairs (1 and 8,
2 and 7, 3 and 6, 4 and 5) and not respect the order?. I think that one can deal with different degrees of freedom and express in different ways the guideline of the system, but it is important at this stage to reveal the infrastructure of this numeric greed so we understand it better and get more out of it. Once we know the rules, we can brake them.
There are still more possibilities of permutation. If we take a tetrachord from the original table levels one, two or four, we can generate 24 permutations for every one because four numbers can be ordered in twenty-two different ways. As I mentioned before, there are only three different tetrachords in the Vedic table, and one more which is the combination of number 3, 6 and 9 (nine is not considered as a pitch).
Lets take for instance the collection 1 2 3 4 from level one. I discovered that it was enough to find twelve different permutations of this tetrachord because the other twelve are the retrograde of the first. These permutations are:
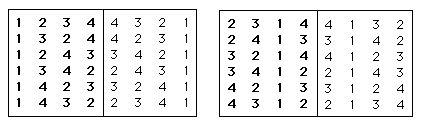
Example 15. Twelve permutations of tetrachord 1 2 3 4 and their retrogrades.
Every one of these twelve permutations generates a new numeric square , which also contains permutations of levels two, three and four. Therefore, in these twelve squares we have all possible permutations of the tetrachords of the Vedic table and more information to engender new musical material. This twelve squares can also be splitted in halve to make other twelve squares as in example 14.
Now i would like to talk more about interpreting this table musically.
As i said before, i want to use a microtonal scale to use this scale, but somehow, i think that i can still do some research on the octatonic scale. Besides using this scale i thought about dividing the piano pitch register in eight parts, using eight different timbers, eight different modes of attack, and eight different dynamics.
I could also have eight different densities, or rhythmical scales for the notes although in this case it may be better to have only four densities because the other four would be the retrograde of the first.
There is no need to assign the pitches of the octatonic scale to the numbers in abstract way as i did it( example I in Appendix). We can choose whatever eight note row and then number the notes. However, it would be nice to choose rows, which are complementary in most ways, as composers do using the serial technique of combinatoriality. This is a way of choosing twelve tone aggregates in which their hexacords hold a mutual relationship. One hexachord can have the following characteristics:
1.- It can map onto its complement under transposition.
2.- It can map onto its complement under inversion.
3.- It can map onto itself under transposition.
4.- It can map onto itself under inversion.
Some of the hexacords in a row have only one of these characteristics and some of them have all of them. Using rows, which are all combinatorial help, us to modulate between different rows in a smooth way. This principle can be applied to the octatonic scale and there is yet need to investigate the different possibilities of combinatoriality in this system.
Another thing to consider is that there are only three octatonic scales and that they share common notes. It is then possible to find a way to modulate from one scale to another in order to expand the use of absolute pitches.

Example 16. The three octatonic scales and their common notes.
See in example 16 how one scale has always four common notes with the other two. Any two scales we play together will then contain the twelve notes of the chromatic scale. One more important thing to notice is that in every scale we can begin with a halve tone or a whole tone. It really does not matter because we keep the symmetry of the scale but the melodic material will change in color. Using the scale that begins with a whole step and assigning the numbers of the table to it, i had a different mode (like major and minor have the same intervalic content but are inverted and sound different). It is important to consider this as a composer.
There is still much to be said about the possibilities to compose with the Vedic Table and the eight tone scale but what I've done up to this moment is enough to start being creative and to explore new possibilities. I now think that to get lost in numbers and devices that seem not to be musical is very important because it is a way of learning how to structure something and how to make your music coherent. All composers have been in a need to do this because dealing with time is a very complex thing. On the other hand there still remains the question of whether we are being too intellectual when we make music in this way and if it is possible to decipher the organization of this music by the listener. I think that it is possible to deal with structural complexity and at the same time to be very transparent or clear. It is true that this music is difficult to understand because we don't have the habit of listening to it but i also think that it is exciting to listen to music that is constructed in ways that we never thought of.