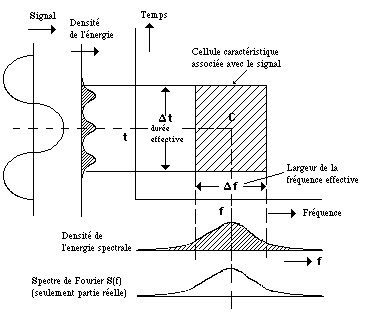
Figure 1.- Rectangle caractéristique d’un signal dans le diagramme d’information.
CHAPITRE I: CONCEPT DE GRANULATION.
I.- Origines scientifiques et esthétiques.
1.- Théorie de la physique quantique de Planck.
"Un système physique peut seulement présenter un numéro fini de différentes états; il bondit d’un état à l’autre sans passer à travers une série continue d’états intermédiaires".
Henri Poincaré
A la fin du XVII siècle il y a eu dans le monde scientifique une grande bataille intellectuelle entre les atomistes, qui croyaient à la segmentation de la matière, et ceux qui pensaient que la matière se comportait d’une façon continue. La vision atomiste de la matière a eu ses origines dans la Grèce antique, où le philosophe Démocrite a proclamé que le monde était constitué de particules ou atomes, tellement minuscules qu’elles ne pouvaient être visibles à l’oeil nu. La grande intuition de Démocrite a été vérifiée scientifiquement sur le terrain de la physique atomique; cependant, la discussion entre les atomistes et les continuistes a persisté jusqu’à la fin du XIX siècle, et cela malgré l'invention du microscope.
C’est le scientifique Hollandais Leeuwenhoek qui à la fin du XVII siècle a construit le premier microscope. Avec cette invention on a pu observer le monde au delà de notre champ visuel, et on a découvert la grande masse de vie concentrée dans une goutte d’eau. Néanmoins, la vision de la continuité renaît, car Leeuwenhoek, au moment d’étudier les spermatozoïdes chez les humains et les animaux pensait qu’ils jouaient un rôle décisif dans la conception, mais il a cru à tort que le spermatozoïde était la seule origine de l’embryon. Or, si le sperme contenait en lui même toutes les caractéristiques non développées du futur embryon, à ce moment-là il devrait également renfermer non seulement les spermatozoïdes du futur être humain, mais aussi les spermatozoïdes des hommes précédents, et ainsi jusqu’à l’infini. Ces spéculations ont conduit les scientifiques comme Leibiniz à croire que "tous les espaces apparents entre les êtres vivants et à leur intérieur étaient eux mêmes remplis avec des êtres vivants de moindre échelle" (Wiener, 1964); pour cette raison, ils ont déduit que la vie pouvait être subdivisée "ad infinitum" et que la matière se comportait d'une façon continue.
Au XIX siècle, certaines idées au sujet de la subdivision infinie de la vie se sont avérées fausses, mais la théorie de la continuité de la matière a persisté, car elle était utile et indispensable pour l’étude de la dynamique des gaz, solides et liquides, et pour la théorie de la lumière et de l’électricité. L’étude de la matière s’établit alors comme la science de la mécanique classique. Clerk Maxwell (Maxwell, j.C. 1871) est l’un des auteurs de la théorie cinétique des gaz ainsi que de la théorie qui explique que la lumière et l’électricité sont transmises comme oscillations continues dans un milieu continu appelé "éther luminescent" ou "radiation". Cette théorie était consistante quand la radiation existait en l’absence de matière, mais elle ne l’était pas s’il y avait une température dans la radiation, car alors la lumière ne pouvait pas trouver un équilibre de température avec la matière. Pour que la théorie de Maxwell fût cohérente, il fallait d’abord une nouvelle découverte.
La première grande transformation de la mécanique classique a eu comme origine la théorie quantique de Planck en 1900 . Planck avait observé qu’il existait une température dans la radiation, et qu'à partir du rapport entre cette température et la nature de la radiation, une loi déterminée s’ensuivait. Cette découverte a eu ses antécédents dans les processus thermodynamiques, comme la distribution de la chaleur dans le spectre de l’énergie radiante. Bunsen et Kirchhoff ont établi l’universalité des propriétés de cette énergie au moyen de leurs études sur l’analyse spectrale, et ils l’ont rendue indépendante de la nature de la substance qui donnait origine à l’énergie. Grâce a l’observation de la radiation lumineuse émise par un corps de métal réchauffé, Planck a constaté que le changement dans la variation de la longueur d’onde de la radiation n’était pas continu, mais discontinu, et il a trouvé une équation mathématique décrivant le rapport entre l’énergie et la fréquence de la radiation au moyen d’une constante (la constante de Planck), de telle sorte que dans n’importe quel processus, la quantité d’énergie émise divisée entre la fréquence de la radiation était égale à cette constante. La magnitude égale à la quantité minimale d’énergie possible, et qui correspond à l’intermittence résultante de la discontinuité de l’émission de l’énergie, a été quantifiée par Planck et dénommée quantum d’énergie. A partir de cette découverte, Planck a constaté que la différence entre divers niveaux d’énergie pouvait seulement se faire par bonds quantiques.
La découverte du quantum d’énergie comme unité minimale indivisible a établi les bases qui ont permis d’affirmer que tout système dans la nature est le résultat de l’arrangement et du réarrangement de parties élémentaires et indivisibles. A partir de cette théorie se développe le langage de la mécanique quantique qui nous décrit les mouvements de la matière et de l’énergie au niveau atomique, et ce langage constitue à l’heure actuelle le meilleur moyen pour décrire la moindre partie de la matière et de l’énergie que l’on puisse connaître.
La théorie quantique a eu des répercussions sur les autres domaines de la physique. En 1905, Einstein avait trouvé que toutes les formes d’énergie radiante telles que la lumière voyageaient dans l’espace en forme des particules quantiques discontinues [1]. Peu de temps après, De Broglie a démontré que les quanta de lumière d’Einstein, ou photons, pouvaient être considérés comme des particules si on les étudiait du point de vue de l’énergie, et comme des vibrations ondulatoires si on les considérait d’un point de vue électromagnétique; il a aussi démontré que des particules atomiques telles que les électrons présentaient des caractéristiques d’ondes sous certaines conditions. D’autre part, grâce à la théorie quantique, Niels Bohr a pu établir sa théorie sur la structure de l’atome lorsqu’il a découvert la même constante de Planck dans la théorie de la radiation de l’hydrogène. Il a aussi démontré que les électrons sautent d’un état d’énergie à un autre par ‘bonds quantiques’ [2].
Des nos jours, le seul concept concret qui nous soit utile pour parler des moindres particules atomiques n’a rien a voir avec quelque chose de matériel, mais avec une constante mathématique, la constante h de Planck (Cesarman, 1972).
2.- Théorie de l’indéterminisme de Werner Heisenberg.
"La partie fondamentale de la nature, sa brique fondamentale de construction serait l’onde-particule ou "partonde" ("wavicle") laquelle serait réduite à une formule mathématique".
Eduardo Cesarman
La physique de Newton veut qu’une particule puisse avoir en même temps une position et un momentum (vitesse). Heisenberg avait observé que dans les conditions où l’on peut déterminer la position d’une particule avec précision, le moment ou la vitesse de la particule ne pouvait être mesurée avec précision, et à l’inverse. Le langage de la mécanique quantique ne nous permet pas de prévoir le mouvement d’une particule en partant de la deuxième loi de Newton, et on ne peut pas établir un rapport de cause entre les forces initiales qui génèrent un mouvement et les mouvements subséquents.
Heisenberg a décrit un système mathématique qui nous a permis d’étudier les phénomènes quantiques dans leur état d’ondes ou dans leur état de particules. Dans ces phénomènes quantiques, il existe de processus où des milliards de particules et d’ondes interviennent, et pour cette raison, s’occuper du devenir d’un seul électron isolé n’a guère de sens. Comme il s’agit d’un phénomène massif, il faut se servir de la statistique et des lois de la probabilité. Ces processus naturels ne peuvent être observes que dans leur ensemble, soit comme particules, soit comme ondes.
La théorie de Heisenberg a déséquilibré la conception déterministe de la physique classique, et son importance a été telle qu'elle a influencé le domaine de la philosophie dans lequel l’idéalisme était revenu avec force. Au cours de ce travail, nous démontrerons l’importance de cette théorie par rapport à la perception auditive et à l’analyse d’un signal sonore représenté de façon granulaire.
3.- Théorie de la perception des quanta acoustiques de Gabor.
En 1947 le physicien mathématicien Denis Gabor écrivait un article pour la revue NATURE intitulé "Quanta acoustiques et la théorie de l’audition". Dans l’article, Gabor a fait une critique de la notion dérivée de Helmholtz selon laquelle l’écoute subjective était mieux représentée par l’analyse de Fourier.
"Qu’est ce qu’on écoute?. Selon les théories de Ohm et de Helmholtz, l’ouïe analyse le son en le décomposant en forme de spectre, et nos sensations se produisent à partir de la valeur absolue des composantes du spectre (composantes de Fourier). Mais l’analyse de Fourier est une description qui ne tient pas compte du facteur temps, et qui considère les composantes spectrales comme des ondes périodiques sinusoïdes exactes de durée infinie. Or, notre expérience le plus élémentaire est que le son est constitué autant par un motif temporel que par un motif de fréquence. La dualité de nos sensations ne s’exprime pas seulement dans la description du son comme un signal en fonction du temps s(t), ni dans sa représentation par composantes de Fourier S(f). Par conséquence, une description mathématique qui tient compte de cette dualité est nécessaire". (Gabor 1947, page 591).
Gabor donne une description mathématique qui tient compte de la dualité du son, et la démontre au moyen du rapport d’un signal temporel s(f) avec un spectre de fréquence S(f) (partie réelle du spectre de Fourier). Après, il graphique une fonction d’énergie de s(t) sur une durée effective &Mac198;t vers une fonction d’énergie de S(f) sur une largeur de fréquence effective &Mac198;f, pour obtenir une cellule caractéristique ou quantum acoustique (Figure 1). Gabor affirme qu'avec ces définitions, la relation mathématique de l’inégalité de Schwarz peut être appliquée:
&Mac198;t&Mac198;f &Mac179; 1, ce qui signifie que l’aire du rectangle caractéristique ou cellule du signal est au moins égale à l’unité.
Gabor établit une équivalence entre son équation &Mac198;t&Mac198;f > 1 et la formulation de l'incertitude de Heisenberg, mais dans ce cas-là, appliqué seulement au rapport entre le temps et la fréquence, et il compare aussi sa formule au modèle classique de la mécanique d'ondes, dans lequel la constante h de Planck serait équivalente à l'unité de son équation. Finalement, Gabor conclut que les quanta du modèle de mécanique d'ondes sont de quanta d'information, et qu'ils peuvent être représentés comme des signaux élémentaires qui ont la forme suivante:
s(t) = exp - a 2(t - t0)2 .exp i2&Mac185; f0t, où a est une constante réel.

Figure 1.- Rectangle caractéristique d’un signal dans le diagramme d’information.
Toujours selon Gabor, "ces signaux élémentaires sont des oscillations harmoniques de type sinus et cosinus de toute fréquence f0 modulée par une pulsation de probabilité, et ils peuvent être utilisés pour représenter des quanta d'information, car un signal arbitraire peut être étendu par leur moyen (avec n'importe quel type d'élection pour la valeur de la constante a). C'est-à-dire, que ce signal peut être étendu en divisant l'information de l'aire en unités cellulaires rectangulaires de n'importe quel aspect &Mac198;t/&Mac198; f = &Mac185; / a 2, et quand on associe chaque cellule à un signal élémentaire avec un facteur complexe d'amplitude cik".
Nous pouvons alors obtenir une méthode d'analyse au moyen d'une matrice (Figure 2), qui contient un langage temporel et un langage de fréquence comme deux cas particuliers extrêmes. Si les cellules sont infinies dans le domaine du temps nous allons obtenir l'analyse de Fourier, et si elles sont infinies dans le domaine de la fréquence nous allons obtenir une expansion de la fonction de s(t)" (Gabor 1947, page 592).
Selon Gabor, le concept du quantum sonore ne peut pas adhérer seulement à des formules mathématiques, car il a aussi une signification physiologique considérable. Le travail de quelques physiciens acousticiens de l'époque a débouché sur la découverte d'un seuil déterminé dans la discrimination auditive pour les différences entre époque et fréquence. Plusieurs expériences qui ont été réalisées par Bürck, Kotowski et Lichte (Bürck, Kotowski et Lichte, 1935) ont démontré que si une oscillation sinusoïdale sonne pendant quelque cycles seulement, notre ouïe la percevrait comme s'il s'agissait d’un bruit, mais qu'avec une durée minimale de 10 millièmes de seconde l'oscillation serait perçue comme une note musicale très courte avec une fréquence bien définie. Une expérience postérieure a porté ses résultats encore plus loin. L'intensité d'une note a été doublée après une période de temps déterminée mesurée a partir du début de la note. Si cet intervalle de temps était inférieure à 21 msecs [3] (s'agissant d'une note de 500 cycles par seconde), on ne distinguerait pas la note d'une deuxième note jouée avec double intensité depuis le début; au delà de ce seuil (21 msecs), les deux notes pouvaient être clairement différenciées. Avec d'autres expériences faites par Shower et Biddulph (Shower et Biddulph, 1931), on a essayé de trouver le seuil de la discrimination de fréquence différentielle de l'oreille. Leur technique consistait à trouver la modulation de fréquence minimale que l'ouïe pouvait reconnaître avec une note de 500 cycles par seconde. Le résultat a été de 2.3 cycles: au-dessus de cette valeur, l'oreille ne pouvait pas distinguer un trémolo d'une note pure.
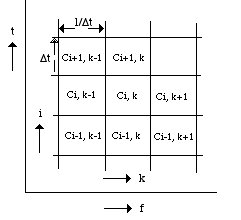
Figure 2.- Matrice des signaux élémentaires qui représentent un signal arbitraire.
Nous pouvons observer que dans toutes ces expériences, le facteur temps aussi bien que celui de la fréquence ont été traités et intimement liés. Ceci conduit Gabor à la conclusion qu'il y a un seuil de perception avec une aire de l'ordre de l’unité, c'est-à-dire, proche à la limite du quantum acoustique, et que ce quantum perceptif était constitué par les variables: temps et fréquence.
Gabor fait ensuite une étude du problème auditif. Il trouve que le seuil de perception ne varie pas beaucoup entre 20 et 250 msecs pour une note de 500 cycles par seconde. Ceci veut dire que dans ces limites, l'ouïe a la faculté de chercher les détails les plus subtils que le motif sonore lui offre. Avec un son pauvre en fréquence, l'ouïe prendra au moins 20 msecs pour la discriminer, et si notre son est prolongé et la largeur de bande est raccourcie de quelques cycles, la discrimination de fréquence de l'ouïe pourra alors suivre ce processus au moins pendant un quart de seconde. Ce qui nous intéresse de ce phénomène est que si l’on essaye de mesurer d'une façon mécanique le changement de la largeur de bande de fréquence du son à travers le temps, on se rend compte qu’aucun résonateur ne sera capable de le faire, car les résonateurs peuvent être accordés pour répondre à des bandes larges ou étroites, mais jamais aux deux en même temps. A partir de ceci, Gabor souligne l'incroyable complexité de l'appareil auditif qui comprend deux mécanismes différents, l'un physiologique (résonateurs auditifs) et l'autre psychologique, probablement situé dans le cerveau. Le deuxième mécanisme est celui qui nous permet de détecter quelques fréquences spectrales d'un son grâce à la possibilité de l'ouïe de dévier l'attention des fréquences ou composantes harmoniques prédominantes.
On peut facilement saisir l'intérêt de Gabor de démontrer sa théorie sur les quanta acoustiques, autant dans une perspective mathématique que dans une perspective de la perception auditive. Cette nouvelle théorie de la représentation sonore est basée sur la théorie quantique de Planck et sur la théorie de l'incertitude de Heisenberg.
Nous verrons au longue de notre travail comment la théorie de la physique quantique et son influence sur les autres sciences et sur la philosophie, continuent d’agir sur la problématique actuelle de la représentation sonore à partir de l'utilisation des méthodes mécaniques d'analyse telles que l'analyse courte de Fourier. Pour l'instant, une des conclusions importantes de Gabor qui servira de base à notre étude, c'est que l'écoute ne peut pas être associée avec un numéro infini de degrés de résolution, mais qu'elle dépend des quanta avec des seuils de différence dans la discrimination de la fréquence, du temps et de l'amplitude.
La finitude de notre perception corrobore l'incapacité de la pensée continuiste pour expliquer les phénomènes psychoacoustiques. D'autre part, c'est seulement avec une vision de la discontinuité de la matière sonore que l'on pourra concevoir un système d'analyse discret qui nous donnera la possibilité de représenter n'importe quel type de signal sonore au moyen de milliers des quanta ou grains acoustiques. Cette représentation-là sera le point de départ pour la création des différentes techniques granulaires dans la synthèse sonore.
4.- D'autres conceptions quantiques du son.
a) Wiener.
En 1964, Wiener présenta un argument similaire à celui de Gabor. Il a opposé la notion quantique de Planck à la théorie diffusée par Leibniz au XVIII siècle sur une conception du temps, de l'espace et de la matière, où le tout était infiniment subdivisé. Le point de départ de Wiener a été une citation de Planck qui nous dit que:
"Aussi bien dans la lumière que dans la matière il existe une texture plutôt granulaire que continue" [4] (Wiener, 1964).
Dans son article "Spatio-temporal continuity, quantum theory and music" [5], Wiener fait une analyse approfondie de l’opposition entre la théorie de la continuité et la théorie quantique de la matière, et il se réfère à la période critique du début du vingtième siècle pendant laquelle la théorie de la physique déterministe a été graduellement remplacé par la mécanique statistique gibsienne, qui a été à l'origine de l’indéterminisme. Wiener a fait une comparaison intéressante entre le système de notation musicale traditionnel et la définition du timbre d'un son dans le temps.
"Dans l'écriture musicale, une note a une valeur de fréquence et une valeur rythmique de durée; pour pouvoir définir le timbre d'un son on doit considérer le nombre d'oscillations (fréquence), plus le devenir de ces oscillations dans le temps. Le problème pour décrire le spectre d'une note c'est que l'interaction entre la fréquence et le temps est extrêmement complexe. L'extension infinie et inaltérée d'une oscillation harmonique simple dans le temps existe seulement en théorie. Commencer et interrompre une note harmonique [6] (telle que la vibration simple d'une corde) produira un effet sur la composition de la fréquence de la note qui peut être minimal, mais l’effet est très réel. Si on veut analyser une note qui dure un temps défini, on doit la décomposer en une bande d'oscillations harmoniques en mouvement, et il faut prendre en considération qu’aucune de ces oscillations ne pourra pas être prise comme la seule oscillation harmonique présente. Une précision temporelle aura comme conséquence un manque de précision des fréquences, et pour obtenir une précision des fréquences on ne devra pas tenir compte du domaine temporel" (Wiener 1964, pages 544, 545).
La conclusion de Wiener constitue le grand paradoxe relié à l'analyse spectrale du son, et il a été peut-être le premier à l'évoquer à la conférence de Göttingen en 1925 [7]. Ce paradoxe existe encore de nos jours, car pour faire une analyse spectrale avec la transformée rapide de Fourier (FFT) il faut choisir entre l'utilisation de fenêtres courtes pour obtenir une précision temporelle, et de fenêtres longues pour obtenir une précision de fréquence, mais on ne peut jamais avoir une précision temporelle et de fréquence en même temps [8]. Le paradoxe de Wiener est basé sur le principe de dualité ou indéterminisme de Werner Heisenberg qui fait allusion à l'impossibilité de déterminer avec précision la position et le momentum d'un électron au même instant.
Les conceptions de Wiener et de Gabor se ressemblent par rapport à l'aspect discret du son. Selon Wiener, les lois et les magnitudes ordinaires ne s'étendent pas dans le cadre du très petit, et il s'avère très important de connaître les limites d'un modèle de mesure.
"Les lois de la physique sont comme la notation musicale, des choses réelles et importantes si on ne les considère pas trop sérieusement et si on ne pousse pas les limites de l'échelle du temps au-delà d'un certain niveau" (Wiener, 1964).
Donc, il y a des limites des bornes du domaine temporel qui s'imposent sur le domaine de la fréquence. Wiener en donne un exemple précis: si on joue la note la plus grave d'un orgue (16 oscillations par seconde) pendant 50 millièmes de secondes, on ne pourra pas percevoir le caractère périodique de la note, seulement une brève poussée d'air. On peut décrire physiquement la fréquence de seize oscillations par seconde (soit 16 Hz) avec une note qui dure seulement 1/20 de seconde (50 msecs), mais on ne pourra pas écouter cette fréquence car il nous faut pour cela avoir plusieurs périodes d'onde (125 msecs pour deux périodes). Avec cet exemple, on revient à l'idée de Gabor du quantum de perception, qui est une particule acoustique dont la perception auditive dépend du rapport entre la fréquence et la durée de cette fréquence. Finalement ils nous faut seulement aborder le travail d’Abraham Moles, car c'est lui qui mènera le plus loin l'idée des quanta de perception.
b) Abraham Moles.
La recherche qui a mené Moles sur la théorie de l'information l’a amené à la conclusion suivante: pour pouvoir définir et déchiffrer un message, qu’il soit visuel ou sonore, on doit prendre en considération les caractéristiques psychophysiologiques du récepteur, car elles seront circonstancielles.
"Un message est un groupe fini, ordonné, d'éléments de perception puisés dans un "répertoire" et assemblés en une structure. Les éléments de ce répertoire sont définis par les propriétés du récepteur" (Moles 1968).
À partir des diverses specialités de la psychophisiologie, Moles a établi trois modalités fondamentales pour les organes sensoriels de l'être humain. La première nous dit que le système récepteur devient insensible quand l'excitation physique captée est au dessous d'une certain limite nommée "seuil de sensibilité". La deuxième se réfère au moment où l'excitation physique dépasse une certaine limite ou "seuil de saturation", et l'organe récepteur ne reçoit plus les variations de l'excitation. Finalement, la troisième modalité nous dit que pour arriver à percevoir un croisement progressif de l'excitation, il est nécessaire que celui-ci surpasse une certaine valeur nommée "seuil différentiel" (Moles 1968, page 26).
Ces modalités nous conduisent de nouveau à la théorie quantique, et si l'on analyse encore les principes de celle-là, on se rappellera que Planck avait constaté que l’écart entre différents niveaux d'énergie peut se faire seulement en bondissant de façon quantique. De la même manière, il est clair que l'organe récepteur ne distingue pas d'une manière continue une sensation d’une autre sensation, mais qu'il bondit grâce à un "seuil différentiel" qui nous permet de passer d'un quantum de perception à un autre.
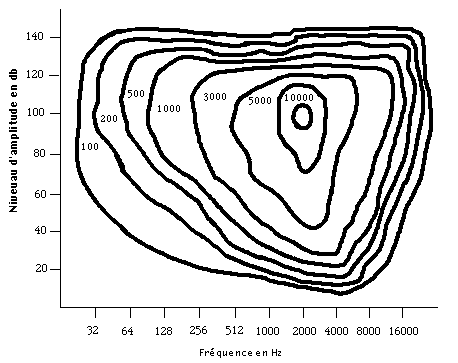
Figure 3.- Carte de l’aire audible dans le plan: niveau de pression sonore vs. fréquence d’ondes sinusoïdales. Les courbes indiquent le niveau d’information acoustique.
L'importance de la théorie de Moles est qu'elle indique l'existence d'un groupe fini d'éléments perceptibles, et que c'est la première théorie à affirmer que le nombre de sensations que reçoivent nos organes psychophysiologiques est quantifiable.
Moles avait segmenté l'espace audible en petites unités avec l'intention de mesurer le contenu de l'information d'un message sonore (Figure 3). Il décrit cette segmentation de la manière suivante:
"On sait que le récepteur, l'ouïe, divise ses deux dimensions (fréquence et amplitude) en quanta. Donc, chaque élément sonore peut être représenté par un carré élémentaire. Un son purement sinusoïdal sans harmoniques, sans limites de duré, pourrait être représenté par un de ces carrés" (Moles, 1968).
Moles a étudié le pouvoir de l'ouïe pour résoudre des petites différences de fréquence et d'amplitude, et il a arrivé à la conclusion qu’il y a des seuils qui quantifient le continu de fréquence et d'amplitude, et donc, qu'on peut parler d'un répertoire d'éléments audibles qui est plus o moins limité à 340,000.
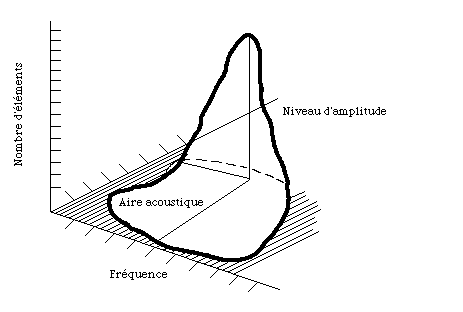
Figure 4.- L’étendue du répertoire des sons purs élémentaires de durée illimitée. Ce répertoire prend la forme d’une montagne car la résolution de l’ouïe est plus grande vers le centre de l’aire audible. La base de cette montagne est circonscrite dans l’aire audible; de cette façon, l’axe vertical nous montre l’habileté de l’ouïe pour résoudre des petites différences de fréquence et d’amplitude.
Observons plus en détail ce répertoire d'éléments audibles ainsi que les "seuils différentiels" qui nous permettent de les percevoir.
"Les seuils différentiels relatifs &Mac198;E/E varient peu autour d'une valeur constante K. La loi de Fechner: &Mac198;E/E = Cte implique la variation logarithmique de la sensation en fonction de l'excitation: S = K log E (Moles 1968)".
Outre cette loi, Moles nous présente deux axiomes en rapport avec la notation en décibels et en octaves:
NdB = 20 log10 A/A0
Noctaves = log2 f/ f0
Avec les trois axiomes précédents il est possible de réaliser le répertoire d'éléments relatifs à une sensation physique donnée. Cependant, il s'avère nécessaire de tenir compte qu'un son pur isolé est défini par trois dimensions, soit physiques: amplitude (pression en Baryes), fréquence (Hz) et longueur (secondes); soit perceptives: niveau (dB), hauteur (octaves) et durée (log t ).
Les "seuils différentiels" de niveau et de hauteur vont varier avec le niveau d'amplitude et avec la hauteur d'un quantum de sensation. Par exemple, les seuils décroissent notamment pour des niveaux moyens (de 50 à 80 dB) et pour des hauteurs moyennes (de 300 à 3000 Hz); pour cette raison, la finesse de l’ouïe sera plus grande dans ces rangs. Autrement dit, les carrés élémentaires qui représentent les quanta de sensation ne sont pas égaux, et leur dimension va décroître vers le centre de l'aire audible, dans laquelle il y aura une plus grande concentration d'éléments perceptibles (Figure 4).
En relation aux "seuils de perception", Moles établit que les seuils en rapport avec les niveaux d'amplitude sont de 2.10 -4 baryes (0 dB) pour le seuil inférieur minimal, de 0.01 atmosphères (140 dB) pour le seuil supérieur de saturation, et de 1 dB pour le seuil différentiel. Les seuils en rapport avec la hauteur sont établis en 16 Hz pour le seuil inférieur, en 16000 Hz pour le seuil supérieur, et en 1 comma (mesure de l'ordre de 0.5 %) pour le seuil différentiel.
La valeur des seuils de durée sera plus difficile à concrétiser, car celle-là va dépendre de la qualité de la fréquence du son en question. Moles définit le "seuil de perception" d'une durée sonore comme "l'épaisseur du présent en deçà de laquelle tous les phénomènes se confondent dans une simultanéité psychologique" et il lui donne une valeur de 50 millièmes de seconde. Selon lui, au-dessous de cette limite, il n’est plus possible de définir la hauteur ou le niveau.
Par rapport au "seuil différentiel" de perception de la durée, Moles le situe en 25 quanta (25 durées différentes perceptibles). Ce nombre nous paraît petit si on le compare au nombre de quanta de fréquence et d'amplitude [9], ce qui signifie que la durée constitue la valeur la plus abstraite et la plus relative dans le domaine sonore.
On peut voir comment la valeur du "seuil de perception" de la durée du quantum sonore de Moles est un peu différente par rapport aux recherches menées par Burck, Kotowski et Lichte. Pour ces derniers, la fréquence d'un quantum sonore est perceptible à partir de 10 millièmes de seconde. Gabor parvient également à des conclusions différentes, car selon lui, pour pouvoir distinguer la hauteur d'un quantum sonore qui est pauvre en fréquence, on a besoin d’au moins 20 millièmes de seconde. La durée minimale d'un quantum sonore de perception est en réalité relative, car elle va dépendre des valeurs d'amplitude et de fréquence. La seul conclusion à laquelle on puisse donc parvenir, c'est que le quantum sonore de perception va se situer entre 10 et 50 millièmes de seconde. Ceci est intéressant, car comme on le verra plus tard, avec les premières techniques de synthèse granulaire on utilisait des grains d'une durée qui oscillait entre ces deux valeurs. Mais on verra également comment on peut utiliser des grains sonores inférieurs à 10 msecs qui seront perçus comme des clicks bruiteux, et des grains sonores supérieurs à 50 millièmes de seconde, qui seront perçus comme des attaques courtes [10] . En effet, il faut distinguer entre la théorie quantique de la perception et l'expérimentation que l'on peut faire avec des grains sonores de durées diverses. Il est certain qu’avec des grains d'une durée inférieure à 10 msecs on aura très peu de certitude par rapport au résultat, et donc, très peu de contrôle, mais l'incertitude peut parfois produire des sons assez intéressants. D'autre part, comment peut-on dire quel est le seuil supérieur d'un quantum sonore, autrement dit, à partir de quelle valeur ce quantum sonore n'est plus un grain?. Il doit y avoir certainement une limite où l’on ne perçoit plus un son comme son granulé, mais comme un groupe de notes superposées. Nous aborderons le sujet de la perception, mais en rapport à des textures granulaires, et nous essaierons d'analyser l'effet de la durée du grain au niveau des groupes de grains considérés comme un ensemble. Pour l'instant, revenons à la définition de Moles de ce que serait l'atome sonore le plus petit imaginable (Figure 5) :
"Un grain de son, l'atome sonore le plus petit imaginable, serait représenté par un son pur élémentaire ou cellule tridimensionnelle, ayant pour côté le seuil différentiel de fréquence &Mac198;F/F, le seuil différentiel d'intensité &Mac198;L/L, et le seuil différentiel de durée &Mac198;T/T" (Moles 1964, page 32).
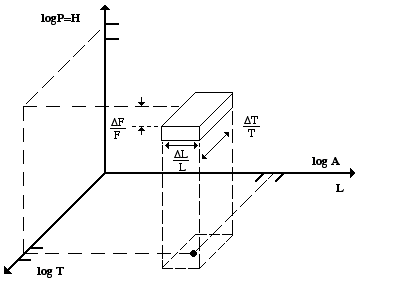
Figure 5.- Les trois dimensions du canal sonore: celles-ci sont portées ici dans un répertoire de domaines: niveau = logarithme des amplitudes, hauteur = logarithme des fréquences, durée = logarithme des temps.
Il est intéressant de comparer cette formulation à celle de Gabor, intéressé aussi par le seuil auditif de perception. Cependant, Gabor n’utilise pas de la même façon que Moles l'idée de "seuil différentiel", mais il établit l'existence théorique du quantum sonore perceptible le plus petit, qui a un seuil avec une aire de l'ordre de l'unité, c’est-à-dire, proche de la limite acoustique du quantum [11]. La formule de Moles est essentiellement la même, mais elle est plus descriptive et précise, car grâce à elle, on peut répertorier le nombre existant de "quanta de sensation".
II.- Application du concept de granulation dans le domaine de la composition musicale.
1.- Première formalisation compositionnelle du concept granulaire.
Iannis Xenakis a été le premier musicien qui ait créé une théorie structurelle de la composition où les grains sonores étaient les éléments constitutifs de base. Son point de départ a été l'idée que tous les sons existants pouvaient être décrits comme un ensemble de particules sonores:
"Tout son est une intégration de grains, de particules élémentaires sonores, de quanta sonores....Tout son, toute variation sonore même continue est conçue comme un assemblage de grains élémentaires suffisamment nombreux et disposés dans le temps d'une façon adéquate....Dans l'attaque d'un son complexe, dans son corps, dans sa chute, des milliers de sons purs apparaissent dans un intervalle de temps &Mac198;t assez court....En considérant la durée &Mac198;t du grain comme assez petite mais invariable nous pouvons la négliger dans ce qui va suivre et ne considérer que la fréquence et l'intensité (F et G). Ces deux natures physiques du son constituent deux ensembles indépendants de par leur nature et elles ont un ensemble produit, le F x G qui est le grain élémentaire de son" (Xenakis, 1971).
La définition d'un ensemble de fréquences et d'intensités dans un moment précis temporel est possible grâce à l'utilisation d'une matrice de coordonnées F et G. Cette matrice (Figure 6) peut être de caractère stochastique, c'est-à-dire, qu'elle peut définir les probabilités d’un grain avec une fréquence F1 et une amplitude G1 pour apparaître dans un moment déterminé dans le temps.
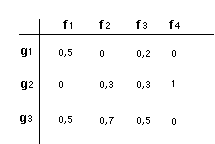
Figure 6
On peut voir dans la figure 7 comment la table d'un ensemble de points qui ont des valeurs F et G nous donne les différentes probabilités de l'ensemble de grains sonores dans un moment temporel &Mac198;t [12]. Si on utilise une série de tables dans le temps, on aura alors l’évolution stochastique de ces grains. Le diagramme suivant définit une série de grains dans un moment temporel &Mac198;t :
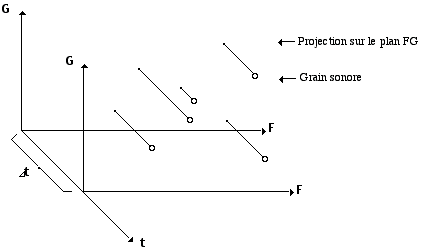
Figure 7
L'innovation de Xenakis par rapport aux définitions précédentes sur le quantum sonore, c'est son intention de créer les bases théoriques pour pouvoir composer des sons complexes en partant d'une distribution aléatoire constituée par des milliers de grains sonores dans le temps. Il appellera cette distribution aléatoire: "nuage de points qui évolue". Cette théorie nous permet de créer des nuages granulaires avec une étendue de fréquence et d'amplitude hors de notre champ d’écoute, mais Xenakis fait référence aux limites psychophysiologiques qui ont été établies auparavant par Gabor et Moles. En tenant compte de ces limites, Xenakis arrive à la conclusion qu’à travers l'utilisation des principes quantiques du son on peut créer des sons entièrement nouveaux:
"Dans les limites humaines et par des manipulations de toutes natures de ces nuages de grains, nous pouvons espérer produire non seulement les sons des instruments classiques, des corps élastiques et en général comme ceux utilisés avec prédilection par la musique concrète, mais aussi des ébranlements sonores avec des évolutions inouïes et inimaginables jusqu’ici. Des structures de timbres et des transformations assises sur des bases n'ayant aucun caractère commun avec ce que l'on connaît à ce jour". (Xenakis, 1971).
Cette citation nous fait penser à Edgar Varèse dans les années 20's, quand il avait prévu l'arrivée d'une musique complètement nouvelle grâce à l'apparition des instruments électroniques [13]. À cette époque-là, Varèse pensait en termes de masse sonore, idée similaire au concept de "nuage granulaire". Le problème est que Varèse ne connaissait pas la notion de grain sonore, et pour ce motif, il ne connaissait pas la notion d'une masse sonore formée par des éléments microscopiques.
Avec la pensée de Xenakis on va rentrer dans une nouvelle période dans l'histoire de la musique, pendant laquelle la production de timbres complexes non instrumentaux devient possible grâce à la synthèse sonore. Dans les années cinquante, l'utilisation de la synthèse additive a constitué un premier essai de production de sons complexes par le moyen d'une addition d'ondes sinusoïdales. Bien souvent, quelques compositeurs de l’époque avaient essayé d’imiter ou de reproduire des instruments acoustiques, et d'autres avaient essayé de créer de sons complètement nouveaux, pourtant, la synthèse additive a été fortement limité par l’absence de l'ordinateur, car on ne pouvait pas considérer l’évolution temporelle indépendante de l'amplitude et de la fréquence de chaque partiel. Dans ce sens-là, Xenakis a fait une critique à cette méthode et à d'autres méthodes de synthèse traditionnelles, dans un moment de l'histoire de la synthèse où le contrôle pour l’évolution temporelle des paramètres était très peu développé.
"Il est fort probable que l’échec des musiques électroniques dans la constitution de timbres nouveaux, mise à part l'insuffisance de la méthode sérielle, est dû en grande partie à la fixité de grains qui engendrent des structures en forme de paquets de spaghetti" (Figure 8) (Xenakis 1971, pg 70).
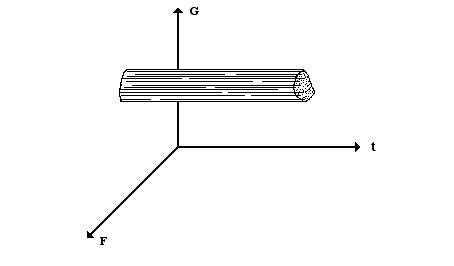
Figure 8
La théorie du quantum sonore appliquée à la musique par Xenakis va ouvrir un nouveau domaine théorique dans lequel il sera désormais possible de synthétiser des timbres analogues aux sons instrumentaux les plus complexes, avec des composantes internes (des grains sonores) qui évoluent dans le temps avec une grande liberté. D'autre part, la proposition de Xenakis de contrôler les grains d'une façon stochastique nous a rapproché de la richesse des sons produits dans la nature, car on a désormais la possibilité de synthétiser des sons aussi intéressants que ceux-là. La justification d'avoir un contrôle stochastique se trouve aussi dans le besoin de créer une technique de synthèse dans laquelle il ne soit pas nécessaire de décrire l’évolution temporelle de chaque grain sonore, car il serait absurde de le faire si l'on tient compte des milliers de grains nécessaires pour créer un son de seulement quelques secondes. On parlera plus tard de la richesse et de la diversité musicale des différents algorithmes stochastiques et non stochastiques avec lesquels on peut générer les grains sonores.
Revenons maintenant aux bases théoriques de Xenakis pour la génération des grains sonores. Il finira par apporter un nouvel élément constitutif de sa matrice, celui de la densité. Ainsi, il définit tout son possible existant comme un son qui peut être coupé en une quantité précise d’éléments &Mac198;F, &Mac198;G, &Mac198;t, &Mac198;D, dans quatre dimensions disposés dans le temps et qui suivent certains règles qui définissent le son et qui sont résumés par une fonction de quatre variables: s (F, G, D, t).
Une fois ce dernier élément défini (la densité), Xenakis propose une unité compositionnelle de haut niveau, dans laquelle les grains sonores seraient organisés en entités nommées trames, qui sont constituées à leur tour par des rectangles occupés ou inoccupés. Ces trames représentent des plans de temps-fréquence dans lesquels se trouvent disséminés des centaines de grains (le nombre de grains est déterminé par un facteur de densité d). Chaque trame est une tranche dans le temps, et un livre de trames constituerait l’évolution d'un objet sonore complexe (Figure 9).
Le travail théorique de Xenakis ne s’arrête pas à la proposition d'un système de composition fait à base de trames granulaires, mais il propose aussi des mécanismes réels pour la génération des grains sonores. D'une part il va décrire une approximation du modèle de Gabor pour des quanta sonores dans le contexte d'une application de synthèse analogique. Le modèle proposé utilise des ondes sinusoïdales de 40 msecs de durée, avec une enveloppe rectangulaire; "la génération de nuages granulaires se fait par mixage de tronçons d'une bande magnétique sur elle même, et on obtient ainsi des densités variantes géométriquement avec comme raison 1,2,3...suivant le nombre de pistes (magnétophones) dont on dispose" (Xenakis, 1971) [14]. D'autre part, il propose la génération de grains à partir d'un ordinateur dans lequel on adapte un convertisseur analogique. Dans ce système, les grains sont produits à partir de formes d'onde programmées par rapport à la théorie de Gabor. Un deuxième programme offre la répartition des grains dans de volumes élémentaires constitués pas l’ensemble d’éléments &Mac198;F.&Mac198;G.&Mac198;t.&Mac198;D., à partir des formules r et r’, avec une fixation de densité moyenne de grains (= nombre des grains par unités de volume).
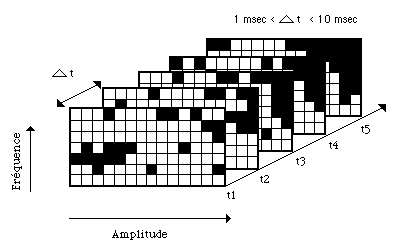
Figure 9.- Un carnet de trames qui contient des grains simultanés.
Chaque trame représente une tranche du temps dans l’évolution d’un son complexe.
Pour la coordonnée t la loi de répartition des grains sur l’axe des temps est: (r) Px = e -ex .dx ou encore, Pxi = e-civ .c.&Mac198;xi Pour les coordonnées G, F, D, la loi stochastique sera:
(r’) f(j)dj = 2/a (1 - j/a) dj ou encore:
Pi = 2/2.10n (1 - i/2.10n - 1)
La proposition des mécanismes qu’utilisent l’ordinateur restera théorique, car ceux-ci n'ont pas été appliqués, et la création d'un système informatique adéquat pour la génération de la synthèse granulaire attendra encore quelques années. Néanmoins, les bases théoriques de Xenakis sur l'utilisation des trames a été d’une importance fondamentale car c'est la première théorie dans laquelle on considère le contrôle des grains sonores d'un point de vue compositionnel. Quand on abordera le contrôle de la synthèse granulaire dans le chapitre 6, on verra en détail les opérations algorithmiques qui sont proposées par Xenakis.
2.- Premiers essais de l'utilisation de la granulation dans la synthèse sonore.
Bien avant la proposition de Iannis Xenakis sur ses mécanismes pour la génération de grains sonores [15], Denis Gabor avait déjà construit en 1946 un granulateur sonore basé sur un système d'enregistrement optique adapté sur un projecteur de cinéma de 16 mm. Avec ce mécanisme (appelé Kinematical Frequency Converter), Gabor avait fait des expériences telles que changer la fréquence d'un son sans changer sa durée, et vice-versa (Roads, 1991) [16] . Ces deux effets ont été réalisés plus tard à travers d'autres techniques beaucoup plus sophistiquées telles que le Vocodeur de Phase, la transformé en ondelettes, le Code linéaire Prédictive (LPC), etc.
Le principe de base de l'appareillage de Gabor a consisté en une segmentation temporelle de sons enregistrés, grâce à une tête rotative (la tête d'enregistrement) qui tournait à travers l'enregistrement du son sur la pellicule ou la bande. Puisque la tête qui tourne est en contact seulement pendant un instant avec la bande, l'effet résultant est l'enregistrement de fragments de son en intervalles réguliers. Ce processus d'extraction de segments ou grains d'un son continu, peut être décrit comme une "granulation temporelle" (Roads, 1991 pg 174). Les segments ou grains enregistrés étaient rassemblés dans une autre magnétophone, et de cette manière on obtenait un son plus ou moins continu avec la même fréquence du son originel, mais avec une autre durée. On pouvait aussi changer la fréquence d'un son sans changer sa durée. Si on voulait par exemple transposer le son par une octave supérieure, il suffisait de produire deux grains dans une même lecture et ensuite, doubler la vitesse du son résultante. Néanmoins, cette façon de transposer le son affectait le timbre original. Les algorithmes de l'analyse de Fourier utilisés par le Vocodeur de Phase constituent la seule manière plus ou moins fidèle de changer la fréquence d'un son sans changer sa duré. Cette technique essaie de reconstruire un signal sonore à partir d'une analyse, et elle fait partie d'une série de techniques de synthèse qui utilisent une représentation granulaire pour générer l'analyse. Plus tard on verra en détail les différences substantielles entre le changement d’échelle d'un son par "granulation temporelle" ou en utilisant le Vocodeur de Phase. On verra aussi comment la "granulation temporelle" est une technique qui va intéresser divers chercheurs et compositeurs, et comment ils vont développer cette technique dans le domaine de la synthèse digitale.
Après la création du mécanisme de granulation temporelle de Gabor et de la proposition de Xenakis d'un modèle possible pour la synthèse granulaire, en 1975 le compositeur et chercheur Américain Curtis Roads essaie de vérifier et d’expérimenter avec les théories du quantum sonore de Gabor, Wiener et Moles, et pour ceci, il construit un système informatique automatisé pour la génération de grains sonores synthétiques. Ceci s’est produit à l'Université de Californie à San Diego, où Roads a utilisé le système informatique Borroughs B6700, avec le programme Music V (Mathews 1969; Leibig 1974).
Les premiers objectifs de ce projet ont été:
"Dessiner et codifier un système de synthèse granulaire, ajuster les paramètres de la synthèse pour atteindre une qualité sonore optimale et une flexibilité, développer des niveaux de contrôle puissants pour la génération des grains, et expérimenter avec la synthèse dans le domaine de la composition" (Roads, 1978).
Dans le système de Roads de 1975, chaque grain sonore avait une durée fixe et une fonction d'amplitude, pendant que les formes d'onde, les fréquences et les amplitudes, étaient variables. Les principaux acteurs de la théorie granulaire avaient suggéré l’utilisation d’une durée pour les grains entre 10 et 60 millièmes de seconde. Après plusieurs essais, Roads arrive à la conclusion que la limite inférieure de la durée du grain devait être de 20 millièmes de seconde. Cependant, il est aussi arrivé à la conclusion que les grains d'une durée de 10 millièmes de seconde étaient efficaces. D'autre part, Roads a admis que l’habileté de l’ouïe pour détecter des événements et discerner un ordre s’étendait sur l’échelle du très petit jusqu’à la durée du grain de un ou deux millièmes de seconde. En fait, c’est le chercheur Green qui a formulé ces limites dans son article "Temporal auditory acuity" publié dans la revue Psychological review en 1971 [17]. Donc, il est possible d'utiliser des grains sonores plus petits de 10 millièmes de seconde, mais l’inconvénient est que plus petit sera le grain, plus on aura besoin de grains pour remplir la durée d'un événement sonore, et ceci implique un coût élevé de temps et de mémoire pour un système informatique. Il faut prendre en considération que le système de synthèse granulaire de Roads utilise des grains synthétiques avec des formes d’onde assez simples. Si on voulait granuler un signal sonore complexe préenregistré, l'utilisation des grains de un ou deux millièmes de seconde déformeraient complètement le signal original, mais il serait toujours possible que l'effet voulu soit justement celui-là. Néanmoins, si le but est d’étirer un son par granulation sans trop modifier son timbre, une limite inférieure de durée de grain s'imposerait entre dix et vingt millièmes de seconde.
Un autre paramètre important du système de Roads est la forme de l’enveloppe du grain. Diverses expériences ont indiqué que la courbe de Gausse n'avait pas un effet d'amplitude suffisant, et que l’enveloppe rectangulaire de Xenakis produisait des "transitoires" non désirables sur la sortie (output) [18]. Par conséquence, Roads a décidé d'utiliser un enveloppe où il a combiné la courbe de Gauss suggérée par Gabor avec le rectangle suggéré par Xenakis, et il a obtenu ainsi un début et une chute légères, et en même temps un sommet soutenu (Figure 10).

Figure 10.- Enveloppe du grain avec attaque et chute Gaussienne, et une portion soutenue d’état stable.
Le système de Roads a été composé par un "instrument" générateur de grains et par un contrôle de haut niveau pour l'organisation des grains. La construction de l'instrument a été assez simple car elle visait seulement à créer les grains sonores, et non à les organiser. Avec cet "instrument" on pouvait varier la forme d'onde, la fréquence et l'amplitude des grains. Dans la version de 1975, les fréquences variaient entre 40.4 et 9.999 Hz avec un taux d’échantillonnage de 20 Khz. La forme d'onde pouvait varier entre chaque grain, et les amplitudes pouvaient varier entre 32 et 72 dB. Les grains avaient une résolution de 16 bits et on pouvait reproduire jusque à 32 grains d'une façon simultanée, et avoir ainsi la possibilité d'obtenir jusqu’à 1600 grains par seconde.
Pour construire la partie du système qui organise les grains, il a été nécessaire de prendre en considération que la quantité de data nécessaire pour une synthèse granulaire plus ou moins dense était énorme, et alors, qu’il n’était pas possible pour le compositeur de spécifier le destin de chaque grain dans le temps [19]. Il était alors nécessaire d'organiser des collections d'unités de haut niveau par l'utilisation de quelques paramètres seulement . Dans le système de Roads, le compositeur travaillait avec des unités appelées événements (Figure 11), caractérisées par les paramètres suivants:
- Temps du début et de la durée du grain (inférieur à 20 millièmes de seconde).
- Forme d'onde initiale et taux de changement (pente) de la forme d'onde entre une onde sinusoïdale à un extrême et une impulsion limitée de bande dans l'autre..
- Fréquence centrale initiale et pente de fréquence.
- Largeur de bande initiale (bandwith), et pente de la largeur de bande.
- Densité des grains initiale et pente de densité.
- Amplitude initiale et pente d’amplitude.
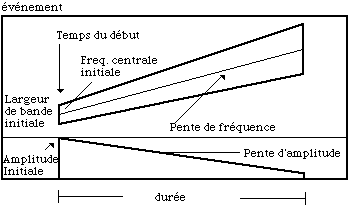
Figure 11.- Paramètres d’un événement.
De cette façon, d'une manière locale, les grains étaient organisés dans le temps au moyen d'un algorithme aléatoire, mais d'une manière globale les grains étaient organisés au moyen des courbes ou enveloppes évolutives qui créaient des nuages granulaires avec densité, amplitude, fréquence, changement de la forme d'onde et de la largeur de bande contrôlables. Le système de Roads est devenu ainsi le premier système de synthèse granulaire avec un potentiel musical, et le premier système qui possédait des paramètres de contrôle qui nous permettaient de composer aussi bien dans le domaine du micro-sonore, que dans le domaine du macro-sonore. Pour pouvoir expliquer cette dernière idée, il est nécessaire de faire une comparaison entre la synthèse granulaire et les méthodes de synthèse traditionnelles. En général, les systèmes de synthèse traditionnels sont dessinés pour générer des sons isolés, qui doivent être assemblés plus tard par le compositeur. Celui-ci doit alors décider comment il disposera de ces sons dans le temps. Par exemple, les sons pourraient être enregistrés sur bande et montés ensuite, ou bien on pourrait créer un programme d’ordinateur automatisé pour leur assigner une position temporelle, mais dans ce cas-là, on parle du rythme et de la durée de plusieurs sons structurés dans le temps, et non plus de la synthèse sonore [20]. Par contre, avec l’application de la synthèse granulaire conçue par Roads, se concrétise pour la première fois un système dans lequel la structure du son synthétisé pourrait être équivalent à la macro-structure d'une composition. Cette idée a été peut-être conçue d'abord par Xenakis, mais Roads a été en tout cas le premier qui a créé un système informatique de synthèse exécutable pour la réaliser. Le mérite de Roads a consisté aussi dans le fait de réaliser un système de synthèse granulaire utilisé par divers compositeurs qui ont pu mener plusieurs essais et développer les possibilités musicales de cette nouvelle technique de synthèse. D'autre part, les possibilités sonores de cette synthèse vont s’avérer très diverses, car la manipulation de la forme d'onde et de la densité des grains peut changer le timbre d'un nuage granulaire d'une façon radical. La seule limitation de ce premier système est l'invariabilité de la durée du grain. Aussi, à cette époque, Roads ne croyait pas nécessaire d’utiliser des grains d'une durée supérieure à 20 millièmes de seconde, ce qui constituait une limitation, car on pourrait parfaitement imaginer une évolution entre des grains minuscules qui sont presque des clicks colorés (grains entre 1 et 5 millièmes de seconde), et des grains qui constituent des petites attaques (à partir de 50 millièmes de seconde), pour en arriver à des grains qui pourraient être considérés comme des petites notes (entre 50 et 100 millièmes de seconde). Un processus de ce type est fort intéressant du point de vue de la composition musicale, puisque un son granulaire qui semble une texture pourrait devenir peu à peu une masse granulaire dans laquelle on percevrait graduellement les contours et certains motifs de fréquence; ensuite, cette masse pourrait se transformer en grains sonores isolés (d’au moins 50 millièmes de seconde) qui pourraient générer une structure rythmique [21]. Ces évolutions continues qui vont de la texture à la masse, de la texture à la fréquence, de la masse aux grains isolés, etc, etc, vont offrir une grande richesse musicale à la synthèse granulaire [22], car si on compare cette technique avec la synthèse additive par exemple, on se rend compte qu’avec la deuxième on ne peut pas produire du rythme puisque chaque oscillateur produit des fréquences continues.
La seule autre limitation du premier système de Roads a été l’absence du développement d’un système de "granulation temporelle" semblable à celui de Gabor, mais ici à partir d'une lecture d’échantillons digitalisés. Toutefois, il est bien vrai que ce type de synthèse était à l’époque beaucoup plus coûteu en termes de calcul de machine. On verra plus tard comment la granulation d'un échantillon aura un potentiel de diversité de timbre majeur que celui de la synthèse à partir d’ondes synthétiques, car on aura avec un échantillon une diversité infinie des formes d'onde complexes pour les grains sonores.
NOTES DE PIE DE PAGE
[1] A ce moment-là, on a considéré que la lumière était constituée par ondes électromagnétiques de caractère continu; cette théorie n’était pas réfutée par Einstein, car De Broglie a confirmé que la lumière pouvait se manifester en forme d’ondes ou en forme de particules quantiques.
[2] La taille du bond dépend du nombre de quanta d’énergie que les électrons ont absorbé ou émis.
[3] msecs est l’abréviation de millièmes de secondes que j’utiliserai au long de ce travail.
[4] Cette citation va influencer énormément les premiers musiciens qui ont utilisé le concept granulaire, comme c’est le cas de Iannis Xenakis.
[5] Wiener, N. 1964. "Spatio-temporal continuity, quantum theory and music". In M. Capek, ed. 1975. The Concepts of space and Time. Boston: Reidel.
[6]. L'auteur fait référence au spectre d'un son composé par des harmoniques naturels.
[7] Dans ce sens là, Wiener serait le précurseur de la théorie quantique du son, car il a précédé Gabor.
[8] Cet aspect sera analysé en profondeur dans la section concernant le Vocodeur de phase (Chapitre 3).
[9] 1200 quanta de sensation de fréquence et 110 quanta de sensation d’amplitude ou niveau, selon Moles.
[10] Dans mes compositions électroacoustiques, j’ai utilisé des grains d’une durée qui va jusqu’à 100 millièmes de seconde. Ainsi, j’ai travaillé dans le continuum entre le rythme et la texture sonore (voir chapitre sur la composition au moyen de la synthèse granulaire).
[11] Voir démonstration mathématique de Gabor dans le chapitre 1, section I-3.
[12] L’ensemble de probabilités est établi au moyen des pourcentages. Par exemple, le grain g1 avec fréquence f1, a 50% de probabilités d’apparaître dans le moment &Mac198;t, et par contre, le grain g1 avec fréquence f3, a seulement 20% de probabilités d’apparaître dans ce même instante &Mac198;t.
[13] "When new instruments will allow me to write music as I conceive it, taking the place of the linear counterpoint, the movement of sound masses, of shifting planes, will be clearly perceived. When these sound masses collide the phenomena of penetration or repulsion will seem to occur. Certain transmutations taking place on certain plains will seem to be projected onto other planes, moving at different speeds and at different angles. There will no longer be the old conception of melody of interplay of melodies. The entire work will be a melodic totality. The entire work will flow as a river flows." Citation de Edgar Varèse (Chow Wen-Chung, 1966).
[14] Xenakis a crée des sons granulaires en utilisant générateurs analogues de fréquences sinusoïdales et tronçons de bande magnétique. Ces sons font partie de sa composition Analogique A-B (Éditions Salabert, Paris).
[15] Voir la fin de la section précédente où j’évoque des propositions de Xenakis.
[16] Dans son article "Asynchronous granular synthesis" (Roads, 1991), Roads spécifie que la compagnie allemande Springer avait construit un magnétophone dans les années 70, basé sur les mêmes principes mécaniques inventés par Gabor.
[17] Dans son article "Asynchronous granular synthesis" (Roads, 1991), Roads parle de ses expériences, où les grains d’une durée inférieure à 2 msecs sont perçus comme un click; pourtant, il affirme qu’il est possible de changer la tonalité de la couleur des clicks en modifiant la forme d’onde et la fréquence des grains.
[18] Une enveloppe rectangulaire a presque le même effet que si l’on n’a pas d’enveloppe. Selon Wishart (1985), si on fait sonner une particule sonore sinusoïdale un instant on aura comme résultat une propagation du spectre au début et a la fin du son, il propose l’élimination de cet effet par l’utilisation d’une enveloppe cosinusoïdale, qui d’ailleurs est très similaire à celui proposé par Roads.
[19] On peut justifier ainsi, comme dans le cas de Xenakis, l’utilisation des méthodes stochastiques ou aléatoires pour le contrôle des grains, mais cette fois à cause d’une problématique de caractère purement pratique.
[20] Dans les systèmes de synthèse granulaire traditionnels par ordinateur, la division entre instrument et partition est typique (comme dans le cas de l’application Csound). L’instrument définit le timbre du son, et la partition assigne la durée, et la position temporelle et spatiale de chaque son. Cette façon de structurer un patch de synthèse est basée sur la pensée traditionnelle de la composition musicale. Bien que la synthèse granulaire se sert d’un instrument (il s’agit d’un instrument très simple qui génère seulement des grains avec une forme d’onde déterminée et une enveloppe), le poids conceptuel se trouve dans le module qui génère la partition. Un grain sonore en lui-même ne signifie rien, et pour cela, on doit tenir compte du rapport du grain avec d’autres grains, ce qui est équivalent à un événement sonore, et cet événement peut constituer autant un son qu’une composition complète. Dans d’autres types de synthèse, un événement pourrait être seulement la génération d’un son isolé, et ceci pourrait difficilement constituer une composition en soi même (sauf pour la synthèse additive, où le contrôle séparé de chaque partiel peut nous conduire à la génération des processus entre différents timbres).
[21] Ceci est en fonction de la densité, car si celle-ci est trop grande, les attaques ne seront pas perçues comme rythme mais comme protubérances d’une masse sonore.
[22] L’aspect du continuum entre différents états de la matière sonore sera développé dans le deuxième chapitre, dans le sixième chapitre, et particulièrement dans le dernier chapitre.