CHAPITRE II: LA SYNTHÈSE GRANULAIRE DIGITALE.
I.- Les différentes méthodes de synthèse granulaire digitale.
Dans le premier chapitre j’ai fait référence à la genèse de la conception du quantum sonore ainsi qu’au début de l’utilisation des techniques granulaires pour la production synthétique du son.
Depuis les premiers essais de Gabor en 1946, et depuis les travaux menées par Xenakis et Roads dans les années soixante-dix, on a développé un nombre considérable de techniques granulaires de la synthèse sonore. Quelques-unes de ces nouvelles techniques ont constitué simplement des prolongements des techniques proposées par Xenakis et Roads, mais d’autres compositeurs ont développé des aspects que ni Xenakis et Roads avaient explorés. Dans les années quatre-vingt, une autre figure importante pour la musique électroacoustique a beaucoup contribué au développement de la synthèse granulaire; il s’agit de Barry Truax, un compositeur canadien qui avait participé au World Soundscape Project crée par R. Murray Schafer à la fin des années soixante et au début des années soixante-dix. L’intérêt de Truax pour l’environnement sonore et pour la complexité des sons qui se produisent dans la vie quotidienne, l’ont mené à chercher une technique de synthèse capable de produire des sons ressemblants [1]. Grâce aux travaux théoriques de Gabor et de Xenakis et aux travaux pratiques de Roads, Truax a réussi a développer sa propre recherche. Sa contribution a été importante puisqu’il il a crée son propre système de synthèse granulaire [2], installé à l’université de SFU en Canada et au studio GMEB de Bourges. Il a écrit plusieurs papiers qui ont été publiés dans diverses conférences et publications importantes, et ses multiples compositions qui utilisent ses techniques de synthèse granulaire ont été jouées dans plusieurs pays du monde. La diffusion des travaux musicaux et de recherche de B. Truax a fait que beaucoup de compositeurs et de chercheurs se soient intéressés à la synthèse granulaire, et au milieu des années quatre-vingt-dix de nouvelles recherches ont été entreprises et ont enrichi davantage l’amalgame des techniques granulaires.
Au début des années quatre-vingt-dix, dans la publication du MIT: "Representations of musical signals", éditée par C. Roads, G. De Poli, et A. Piccialli [3], divers articles sur les différentes représentations du signal ont été recueillis, notamment ceux qui concernent les représentations granulaires. Dans l’article "Asynchronous granular synthesis" (Roads, 1991) de Curtis Roads, celui-ci aborde les fondements de la synthèse granulaire, et propose une classification des méthodes granulaires qui va dépendre de la façon selon laquelle on organise les grains. Puisque je considère que Roads est la personne qui a le plus réfléchi à l’aspect théorique des techniques granulaires, je respecterai sa classification, et je l’utiliserai comme point de départ. Je ferai ensuite quelques commentaires, et je suggérerai quelques modifications, mais pour l’instant, j’estime que sa vision est claire et très utile pour se faire une idée de l’étendue des techniques granulaires.
1.- Classification des méthodes de synthèse granulaire par Roads.
"Le grain est une représentation particulièrement apte et flexible pour le son musical, car il combine l’information du domaine temporel (temps de commencement, durée, forme d’enveloppe, forme d’onde) avec l’information du domaine de la fréquence (la fréquence de l’onde qui comporte le grain). Ceci est en opposition aux représentations basées sur l’échantillon, qui ne capturent pas de l’information du domaine de la fréquence, et des méthodes abstraites de Fourier qui prennent compte seulement du domaine de la fréquence" (Roads, 1991).
Voici à nouveau la thèse du quantum acoustique de Gabor. Le grain est une entité apte pour la représentation d’un signal sonore car il contient les deux aspects essentiels: le domaine de la fréquence et le domaine temporel. Roads se sert de cette thèse pour confirmer la flexibilité de la représentation granulaire, et pour expliquer comment ont été développées des propositions qui peuvent se diviser d’abord en deux grands groupes: l’un comprend les techniques qui réalisent la modélisation des sons traditionnels instrumentaux et vocaux, et l’autre, les techniques qui n’ont pas besoin d’une analyse a priori. Pour le premier groupe, Roads fait référence aux techniques d’analyse-synthèse, où une analyse spectrale est effectuée sur un signal sonore pour réaliser ensuite une re-synthèse. Il y a plusieurs façons d'analyser les sons et de les décomposer en éléments de base, de manière à les remettre ensemble pour avoir une bonne copie des sons originaux. Mais on pourrait altérer les éléments obtenus par l'analyse avant d’effectuer la re-synthèse (Voir Risset et Wessel 1982, 1991). Le deuxième groupe concerne les techniques de synthèse qui peuvent générer des centaines ou des milliers de grains par seconde et les déployer dans l’espace temps-fréquence, et qui ne se servent pas forcement d’une modélisation instrumentale ou vocale (ni d’une analyse). Les méthodes qui appartient à ce groupe sont: QSGS (Quasi-syncrhonous Granular Synthesis), AGS (Asynchronous Granular synthesis) [4] et la granulation temporelle presque synchrone ou asynchrone d’un ou plusieurs échantillons. Dans ce chapitre on parlera plutôt de ce deuxième groupe, car le troisième chapitre est consacré aux techniques granulaires d’analyse-synthèse.
Il faut d’abord revoir les concepts fondamentaux pour la génération de grains dans la synthèse AGS (voir fin du premier chapitre). Les éléments de base pour la création d’un grain acoustique sont: durée du grain, enveloppe, forme d’onde, fréquence, amplitude, et localisation dans l’espace. On a déjà parlé dans le premier chapitre de la durée du grain en rapport avec la fréquence et la perception psychoacoustique, et on a établi des limites et des seuils auditifs. Comme on a déjà vu, il es possible d’essayer des durées allant jusqu’à un millième de seconde ou même moins, mais plus petite sera le grain, plus longue sera aussi le calcul pour l’ordinateur, car il faudra une quantité plus importante de grains pour remplir une seconde. Donc, en général, on fera varier la durée du grain entre cinq et cent millièmes de secondes. Moles par exemple (1968), avait établi la limite supérieure à soixante millièmes de secondes mais j’ai déjà évoqué mes raisons d’aller au delà et d’utiliser des grains qui se rapprochent aux notes (voir fin du premier chapitre).
On a également cité les premières enveloppes utilisées par Gabor, Xenakis et Roads (enveloppe Gaussienne, enveloppe rectangulaire, enveloppe Quasi-gaussienne). Il y a cependant d’autres enveloppes possibles comme le triangulaire, le hanning, le trapézoïde, etc, mais leur utilisation va dépendre de plusieurs facteurs. Par exemple, si l’on veut faire de la synthèse granulaire en temps réel, il faut utiliser de simples segments de ligne pour économiser de la mémoire (Fig. 1E) (Truax 1987, 1988).

Figure 1.- Enveloppes du grain. (a) Gaussienne. (b) Quasi-gaussienne. (c) Hanning. (d) Trapézoïde. (e) Triangle.
D’autres enveloppes peuvent être utilisées pour modifier la qualité du timbre; une enveloppe rectangulaire aura un attaque plus pointue qu’une enveloppe hanning (Fig. 1C). Cette dernière est d’ailleurs utilisée en conjonction avec la transformée de Fourier rapide (Roads, 1992). On peut également expérimenter avec d’autres types d’enveloppes et choisir celles qui nous intéressent par rapport à l’effet qu’elles produiront sur le son. Il faut prendre en considération que la forme de l’enveloppe va moduler le son et donc, qu’elle va modifier le timbre du son. Certains enveloppes comme l’enveloppe rectangulaire produisent des transitoires, c’est-à-dire, des effets spectraux parfois indésirables. Pour résoudre ce problème on peut attacher un filtre bandpass à la sortie de notre instrument granulaire pour les éliminer (Roads, 1991). Les différentes nuances de timbre crées par l’enveloppe utilisée nous permettent d’effectuer des modulations entre les différentes enveloppes pour obtenir ainsi des changements de timbre sur les grains. En général, on utilise toujours la même enveloppe pour tout un processus de synthèse, et on ne profite pas assez de la possibilité d’une variation temporelle, probablement à cause du délai de calcul (particulièrement pour la synthèse granulaire en temps réel). Dans le projet GiST développé à l'IRCAM par Gerhard Eckel et moi même, j’ai pu tirer profit des caractéristiques du grain FOF (Fonction d’onde Formantique) pour moduler l’enveloppe du grain d’une façon constante et continue, avec des résultats très intéressants (Eckel, Rocha Iturbide, 1995). Cette technique utilise la station ISPW de l'IRCAM et elle fonctionne en temps réel. On parlera du projet GiST et de ces expériences plus tard. Pour finir avec les considérations générales sur l’enveloppe, il faut dire que la durée et l’enveloppe du grain sont indépendantes de la fréquence, mais qu’exceptionnellement elles pourraient en dépendre (des courtes enveloppes pour de fréquences aiguës, et des longues enveloppes pour des fréquences graves). C’est le cas de la technique granulaire d’analyse-synthèse par ondelettes dont on parlera dans le troisième chapitre.
La forme d’onde va affecter d’une façon radicale le timbre du grain. On peut créer alors des évolutions de timbre qui vont d’une onde sinusoïdale simple et qui passent par l’utilisation d’ondes qui ont une composition spectrale de plus en plus dense (davantage de partiels) jusqu’à des pulsations de bande limitée (Roads, 1991). On peut aussi varier la forme d’onde par FM, par AM ou par modulation en anneau. En fin, il y a plusieurs possibilités de faire varier la forme d’onde avec des simples formules mathématiques (Jones et Parks, 1988). D’autre part, on peut aussi utiliser des formes d’ondes prises sur les échantillons des sons enregistrés. Cette technique a donné lieu à un groupe bien spécifique de synthèse granulaire qu’on appelle aujourd'hui Granular Sampling (Lippe, 1993) [5]. Comme on a vu dans le premier chapitre, la technique a été introduite il y a déjà longtemps par Gabor avec son système d'enregistrement optique (Gabor, 1946).
Le choix de la fréquence, l’amplitude et la localisation dans l’espace de chaque grain, sont davantage en rapport avec des notions d’esthétique, mais toujours liés à la perception. Par exemple, un changement d’amplitude sur les grains produit une impression de volume, alors que si on utilise une amplitude constante, on aura un son plus aplati. Je développerai davantage ceci un peu plus loin. Commençons par définir ce qu’est le générateur fondamental de grains selon Roads:
"L’instrument granulaire de base est un oscillateur d’onde sinusoïdale contrôlé par une enveloppe génératrice avec une pente gaussienne" (Roads, 1991) (figure 2).
Puisque cet instrument est très simple, la complexité du son dérivé de la synthèse dépendra de la quantité de données de contrôle, c’est-à-dire, de la façon de contrôler la fréquence, l’amplitude, la forme d’onde, etc, de chaque grain. Cette complexité va également dépendre de la quantité de grains que l’on déclenchera par seconde (densité), et si on les déclenchera d’une façon continue ou discontinue (Quasi synchronous streams et Asynchronous clouds). Il y a donc plusieurs façons d’organiser les grains dans des unités musicales de haut niveau qui sont en rapport avec le contrôle de l’information, et qui vont donner différentes techniques ou méthodes de synthèse granulaire. Roads va proposer une classification de ces différents méthodes:
• Grilles et écrans Fourier/Ondelettes
• Chevauchement des flots de fréquence-synchrone
• Flots presque-synchrones
• Nuages asynchrones
• Flots et nuages des sons échantillonnés et granulés dans le temps, avec chevauchement presque synchrone, ou asynchrone sep tape.
Dans ce chapitre, je détaillerai les trois dernières méthodes de synthèse (Flots presque-synchrones, nuages asynchrones, et granular sampling [6] synchrone ou asynchrone) car ils appartiennent au même groupe de techniques granulaires qui n’utilisent pas l’analyse-synthèse. Toutefois, les méthodes de synthèse granulaire par flots presque-synchrones qui utilisent des ondes synthétiques ou la granulation d’un échantillon, pourraient également être considérées dans un troisième groupe qui n’appartient ni aux techniques granulaires d’analyse-synthèse, ni aux techniques asynchrones. On pourrait les considérer alors comme des cas particuliers d’amplitude modulée (Roads, 1992), et les comparer aussi à des techniques de synthèse formantique (si on traite le grain comme une fonction d’onde formantique). J’aborderai ces derniers dans le quatrième chapitre, car mon projet de recherche principal s’est rattaché à l’utilisation des FOF [7] (Rodet 1980) pour la synthèse granulaire (Eckel et Rocha Iturbide, 1995). Nous verrons maintenant certains aspects de la synthèse granulaire presque-synchrone; l'étude des deux premières méthodes (Grilles et écrans Fourier/Ondelettes et Chevauchement des Flots de fréquence-synchrone) [8] fera partie du troisième chapitre.

Figure 2.- Instrument granulaire simple. Oscillateur sinusoïdal contrôlé par une enveloppe génératrice en forme de gausse.
2.- Synthèse granulaire presque synchrone.
Avec la synthèse granulaire presque synchrone (QSGS) [9], il s’agit de générer un ou plusieurs flots de grains, chaque grain suivant un autre grain, avec une délai variable entre chaque grain. Cette période de délai peut être plus ou moins régulière, et c’est pour cette raison que Roads appelle cette technique "presque synchrone". Quand la période de délai est régulière, on obtient une fonction périodique et il est possible d’analyser la QSGS comme un cas particulier d’amplitude modulé (Fig. 3). Cet type de modulation apparaît lorsque la forme d’un signal (modulateur) détermine l’amplitude d’un autre signal (porteur). La modulation va créer une série de sidebands qui s’ajoutent au spectre final de la forme d’onde du grain. Le modulateur constitue l’enveloppe du grain, et sa forme va déterminer l’amplitude des sidebands . L’inversion de la période de la fonctionne de l’enveloppe produira la fréquence de ces sidebands . Par exemple, avec des grains d’une durée de 20 millièmes de seconde, les sidebands auront un écart de 50 Hz (fig. 4).
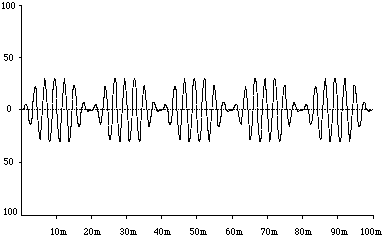
Figure 3.- Flot de grains équidistants avec un délai constant. Leur durée est de
20 msecs, leur fréquence centrale de 353 Hz, et ils ont une enveloppe Hanning.
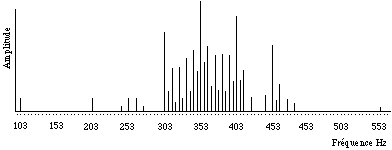
Figure 4.- Spectre du grain de 20 msecs, avec une fréquence centrale de 353 Hz
et une enveloppe Hanning. On peut voir de sidebands tous les 50 Hz avec des
amplitudes différentes.
Le résultat d’une modulation de ce type crée une région formantique autour de la fréquence de la porteuse; ces régions formantiques sont typiques de la voix et de certains instruments acoustiques résonants. Selon Roads, la synthèse QSGS est similaire aux méthodes de synthèse formantique comme VOSIM (Kaegi et Templaars, 1978) et CHANT (Rodet, 1980 et Rodet, Potard, Barrière, 1984). Si on souhaite travailler sur l’aspect formantique en particulier, il est préférable d’utiliser les techniques conçues pour cela; on peut également contrôler avec finesse le résultat spectral voulu, mais l’avantage de la synthèse QSGS sur les techniques formantiques est la possibilité de mélanger des flots réguliers (formantiques) et des flots irrégulières (où on ne peut plus prévoir le résultat formantique) [10]. Cependant, on pourrait aussi avoir un contrôle irrégulier sur les grains dans la synthèse formantique (CHANT [11] et VOSIM); c’est justement ce que j’ai réalisé dans le cadre du projet GiST à l'IRCAM (Eckel & Rocha Iturbide, 1995). Je m’étendrai davantage sur la synthèse granulaire formantique dans le quatrième chapitre.
Le compositeur Barry Truax avait mis à l’épreuve la synthèse QSGS [12] avec plusieurs flots (voix) en parallèle [13] depuis 1988 (Fig. 5). Il cherchait à contrôler l'épaisseur de la texture sonore au moyen de la création d’un flou sur la structure formantique (Truax 1987, 1988). En partant de la prédiction de Roads sur l’amplitude modulée quand on produit un flot régulier (Roads, 1985), Truax avait aussi pris conscience qu’il existait un continuum entre des sons affectés par une amplitude modulée, où il n’y a pas de variation de délai entre les grains, et des sons où il y a une variation de délai qui produit des "textures stochastiques":
"Le délai entre les grains peut être utilisé en conjonction avec l'effet AM, car il va changer la périodicité globale du son résultant. Le temps de délai minimum est de 0, et pendant que ce temps s’accroît jusqu’à atteindre une fraction significative de la durée du grain, il est possible d’écouter divers effets de modulation. Plus longue sera le délai, plus la sensation de la texture commencera à se perdre jusqu’à aboutir à des délais très longs où le grain sera perçu comme un événement séparé" (Truax, 1988).

Figure 5.- Description graphique de la synthèse granulaire presque synchrone avec trois flots de grains en parallèle qui ont un délai variable. Puisque chaque flot peut avoir une fréquence différente, il serait possible de recréer les trois régions formantiques nécessaires pour créer un son ressemblant à celui de la voix.
Ce continuum est très important, car à vrai dire, si on fait de la synthèse granulaire en tenant compte de lui, il n’y aurait aucun besoin de séparer la synthèse QSGS et la synthèse AGS (Asynchronous granular synthesis). En fait, l’existence de ce continuum m’a amené a réfléchir sur les possibilités de trouver une technique de synthèse qui nous permettrait de travailler sur le domaine spectral et sur le domaine temporel du son en même temps [14]. On pourrait dire que la répétition régulière des grains donne lieu à des régions formantiques, et qu’il s’agit donc d’un effet avec une prépondérance spectrale. Quand on commence à altérer cette régularité, on se trouve toujours dans le domaine spectral, mais on perd le contrôle sur le résultat formantique, et il y a un problème de désynchronisation de phase entre les grains qui vont produire des annulations et des renforcements d’amplitudes. Une fois que la quasi synchronie devient de plus en plus irrégulière (à ce moment-là on peut parler de synthèse AGS), on entend d’abord différents types de "textures stochastiques", et on entend ensuite les grains comme des événements séparés. Ceci est une description simplifiée du continuum entre la périodicité et la discontinuité des grains, mais en réalité il y a une grande variété d'effets psychoacoustiques qui peuvent avoir lieu selon la durée des grains, leur fréquence, leur enveloppe, la densité du flot, etc, et les différentes combinaisons de tous ces éléments. Plusieurs acousticiens ont fait un étude des ces étapes intermédiaires. McAdams et Bergman (1979) ont décrit des événements sonores d’une grande densité avec le terme de streaming , ou l’on peut percevoir des événements isolés, groupés dans des flots, ou fusionnés. John MacKey (1984) a également décrit les événements sonores avec une augmentation de densité; ceux-ci créent un spectre d’impressions qui passe d’une simple séquence de fréquences à un flux , à un grouillement, à une bande de texture fusionnée , et finalement à une masse sonore. MacKey a aussi décrit le continuum en termes d'augmentation de bandwidth [15].
Nous entrerons plus en détail sur les diverses étapes du continuum dans la prochaine section sur la AGS, mais particulièrement dans le quatrième chapitre, où j’expliquerai diverses expériences dans ma recherche sur l’étendue du continuum en utilisant la synthèse granulaire avec grains formantiques (FOF). Toutefois, je voudrait établir déjà les bases théoriques qui nous permettront de bien définir ce continuum qui constitue la liaison entre la QSGS et la AGS.
Denis Smalley (compositeur néo-zélandais) a bien établi la différence entre les deux domaines du son: le spectral et le morphologique (Smalley, 1986). Il a aussi bien défini le lien entre ces deux domaines en proposant deux différents types de continuums. Il a pris conscience de l’importance de l’élément psychoacoustique pour pouvoir établir les étapes intermédiaires d’écoute dans les continuums [16]. Le problème qui se pose lorsque l’on commence à théoriser sur ces continuums c’est que l’on quitte le domaine de la fréquence pure pour se retrouver dans le domaine du timbre. Or, on sait bien qu’on ne peut pas cataloguer le timbre avec les mêmes paramètres théoriques de la musique traditionnelle, car il n'est pas un élément mesurable et linéaire comme la durée et la fréquence d'une note, lesquelles peuvent être représentées sans difficulté par une notation [17]. Pour cette raison, la classification du timbre présente encore un problème pour les théoriciens. Néanmoins, l'approche de Smalley est importante car il crée un système plus flexible.
Smalley commence par créer une typologie spectrale. Il définit le mot "spectre" comme la totalité des fréquences perceptibles, et conclut avec la division du domaine de la fréquence en "ton" et en "timbre". Il affirme aussi qu'une typologie spectrale ne peut pas être séparée du domaine du temps. Smalley conçoit un schéma dans le domaine du continuum qui va de la "note" au "bruit". Dans ce schéma il y a trois points centraux de référence, la note qui est divisée en note propre, spectre harmonique et spectre inharmonique, le noeud et le bruit (fig. 6). On commence par la note propre qui est un ton avec une fréquence pure et bien définie (note instrumentale), où l’on donne plus d’importance à la hauteur qu’au timbre. Suit le spectre harmonique, où l’on commence à percevoir les harmoniques naturelles comme une extension de la fréquence pure de la note. La perception de ces harmoniques varie selon le type de son que l’on écoute (il y aura des sons harmoniques plus ou moins riches). La dernière division du domaine de la "note" est le spectre inharmonique; celui-ci réunit les sons qui peuvent être semblables aux sons harmoniques (spectres plus ou moins harmoniques qui ont d'autres intervalles), et les sons qui ont peu de relation avec les spectres harmoniques, comme c'est le cas d'un son de cloche. Ensuite, nous avons le deuxième groupe caractérisé par le spectre nodal. Ici, il y a une bande de fréquences rechargée qui résiste à l'identification auditive de ses différents composants. Un exemple peut être le son d'une cloche écouté dans le lointain, ou une grappe de sons ("cluster"). Le spectre nodal se trouve au seuil du domaine du "bruit", et la seule façon de savoir que l’on se trouve dans ce nouveau domaine est lorsque la densité du spectre est tellement comprimée qu'il est impossible d'entendre la structure interne des fréquences. Le "spectre" du bruit va être aussi riche et varié que les autres.
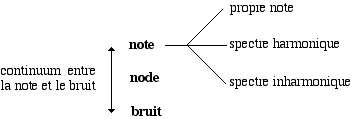
Figure 6.- Topologie spectrale.
Smalley caractérise le seuil où l’on ne peut plus écouter les différents partiels d'un son comme effluvial state (état effluvial). Confronté à cet état, l'auditeur a besoin de déplacer son centre d'attention de la structure interne des composants du son et de suivre le "momentum" de la forme extérieure de ce son.
Pour en revenir à ce qu’on a dit sur la synthèse QSGS, il serait possible de comparer les différentes étapes qui créent le lien entre la QSGS et la AGS à la théorie de Smalley, si l’on crée un processus de synthèse granulaire allant de la note au bruit. Le domaine de la note serait celui où il y a des grains avec un délai régulier. Imaginons des grains de 50 msecs avec une fréquence de 320 msecs qui ont d’abord un délai de 500 msecs entre eux; à ce moment on écoutera simplement la fréquence du grain (note propre). Ensuite, si on commence à réduire le délai entre les grains jusqu’à atteindre 50 msecs, on aura une écoute de la même fréquence, plus un spectre harmonique (les sidebands de 20 Hz générés par la AM constituent des harmoniques de notre fréquence centrale). Ensuite, on pourrait ajouter d’autres flots de grains de 50 msecs avec d’autres fréquences centrales (qui ne soient pas des multiples des sidebands de 20 msecs) et entrer dans le domaine inharmonique; si on commence à désynchroniser la régularité des flots, il y aura d’autres effets de modulation AM et des effets de modulation de phase, qui enrichiront ainsi le domaine inharmonique. Si l’on augmente la densité et l'irrégularité des délais, et si on commence à faire varier la fréquence de chaque grain d’une façon stochastique, il y aura un moment où on parviendra à l'état effluvial de l’écoute, où il ne sera plus possible de se concentrer sur la structure spectral du nuage granulaire; nous serons alors forcés "de changer notre centre d'attention de la structure interne des composants du son et de suivre le "momentum" de la forme extérieure de ce son" (Fig. 7).
A partir du moment où l’on n'écoute plus la structure interne d'un son, on entre dans le domaine de la "morphologie". Il se peut que la synthèse AGS commence lorsque l’on entre dans ce domaine, mais il est difficile d’établir ceci d’une manière précise. En ce sens, le fait de classifier et de diviser les techniques de la synthèse granulaire (sans prendre compte des techniques d’analyse-synthèse et de synthèse granulaire synchrone) en QSGS et AGS pose un problème. Il vaudrait peut-être mieux contempler ces deux méthodes dans la même catégorie, et utiliser les deux techniques avec le même instrument granulaire pour profiter de la richesse de deux mondes (spectral et morphologique) et de leur continuum, où il est possible de passer constamment d’un état à l’autre. Ceci constitue ma proposition personnelle élaborée et développée dans le projet GiST déjà mentionné, que je traiterai en profondeur dans le quatrième chapitre.

Figure 7.- Processus granulaire entre la QSGS et la AGS.
Smalley donne une autre définition du continuum en allant dans le sens inverse. Il fait sa proposition en partant du domaine morphologique, où il y a des événements séparés qui pourraient être des gros grains [18] isolés dans le temps avec des attaques différentes (différentes enveloppes). Il s’agit ici de petites notes avec des délais qui constituent des rythmes. Que se passe-t-il si on commence à resserrer les délais?. Eh bien, on entrerait peu à peu dans un attack effluvium continuum, c'est-à-dire, un continuum temporel où différentes attaques séparées deviennent de plus en plus comprimées, donnant une différence de timbre. Ici on va graduellement de la séparation des attaques à leur répétition, ensuite à la perception de grain où les impulsions individuelles ont perdu leur identité, et finalement à la disparition du grain qui éventuellement peut devenir une fréquence définie (quand l'attaque qu'on répète est très courte). Une fois de plus, Smalley crée un schéma global dans le domaine du continuum où le contexte de notre écoute est très important, mais cette fois dans le domaine de la temporalité (Fig. 8).

Figure 8.- "L’attack effluvium continuum".
La conception de Smalley sur le continuum, vue à partir d’une perspective spectrale et à partir d’une perspective temporelle, nous fait entrer à nouveaux dans la théorie quantique du son, et on se rend compte qu’on ne peut pas séparer les domaines spectral et temporel, puisqu’ils constituent tous deux une partie essentielle du son. Néanmoins, il est vrai que tout comme la lumière se comporte parfois de façon ondulatoire, ou parfois comme un ensemble de particules (photons), le son fait de même; il est parfois plutôt spectral, parfois plutôt morphologique. Le paradoxe se pose à nouveau.
Dans la synthèse granulaire QSGS comme dans la physique quantique, on ne sait pas avec certitude quand une particule se comportera d’une manière ou d’une autre (comme un électron qui change d'état d'énergie dans l’atome d’une façon complètement aléatoire). D’autre part, la particule aura des caractéristiques dans les deux domaines, mais il nous sera presque impossible de la situer dans le continuum.
"Presque tous les électrons, ainsi que d’autres entités subatomiques ne sont tout à fait ni des particules ni des ondes, mais plutôt un mélange confus des deux, bien connu comme un paquet d’onde (wave packet). C’est ici que la dualité de la particule-onde et le mystère de la théorie quantique se réalisent" (Zohar, 1990).
Les différentes caractéristiques de la théorie quantique peuvent s'appliquer au champ sonore en général. J’ai déjà parlé dans le premier chapitre du principe d’incertitude de Heisenberg, où l’on peut mesurer la position exacte d’un électron quand il se manifeste comme une particule, ou mesurer son momentum (vélocité) quand il s’exprime comme une onde, mais où on ne peut pas mesurer les deux exactement en même temps. La théorie quantique abonde en inexactitudes et incongruences de ce genre, de même que le comportement du son dans le continuum. En ce sens, je crois que la théorie spectro-morphologique de Smalley s’adapte bien à la théorie quantique du son, et pour cette raison, elle sera la théorie de base sur le continuum que j’utiliserai pour fonder ma recherche.
Pour conclure cette section, il faut dire que malgré la richesse sonore de la synthèse QSGS et du continuum dont j’ai parlé, il ne peut y avoir un contrôle précis sur le résultat spectral lorsqu’on commence à désynchroniser les grains, car on perd toute contrôle sur la phase. On peut obtenir des effets fort intéressants, mais ils seront le résultat d’une expérimentation plutôt intuitive. Seules les techniques granulaires d’analyse-synthèse permettront d’avoir un contrôle exact du résultat, mais elles auront d’autres désavantages, et en conséquence, on ne peut avoir de préférence pour elles. Je traiterai ces techniques dans le troisième chapitre, afin d’établir une comparaison plus précise.
3.- Synthèse granulaire asynchrone en partant des ondes synthétiques.
"Dans la synthèse granulaire asynchrone le concept linéaire des flots de grains est abandonné. Les grains sont distribués d’une façon statistique sur une durée spécifique dans des régions inscrites sur le plan temps-fréquence. Ces régions sont appelées nuages, unités avec lesquelles un compositeur travaille" (Roads, 1992).
Voici la description de la "Synthèse granulaire asynchrone" (AGS) qui fait Roads dans son article "Asynchronous granular synthesis" [19]. C’est la première fois qu’il parle des nuages granulaires. Il décrit ensuite les paramètres qui vont affecter les caractéristiques sonores de ces nuages, mais ils ne sont pas très différents des paramètres décrits dans son article "Granular synthesis of sound" de 1981 (voir premier chapitre). Je les décrirai de toute façon, et j’abonderai également d’autres approches pour générer les nuages granulaires et établir ensuite une comparaison.
a) Contrôle des paramètres des nuages granulaires.
Roads définit les paramètres de la façon suivante (Fig. 9):
1.- Temps du début et durée du nuage .
2.- Durée du grain (De 5 à 50 msecs mais peut-être au-dessus, ou au-dessous de ces limites).
3.- Densité de grains par seconde; cette densité peut varier pendant la durée du nuage. La densité maximale dépend de la spécification de l’application.
4.- Bande de fréquence du nuage; spécifiée en général par deux pentes qui forment deux bornes de fréquence (inférieure et supérieure), entre lesquelles les grains sont éparpillés; alternativement, les fréquence des grains dans un nuage peuvent être limitées à une série spécifique de hauteurs.
5.- Enveloppe d’amplitude du nuage.
6.- Forme d’onde des grains.
7.- Dispersion spatiale du nuage, où le nombre de chenaux dépend des spécifications de l'application.
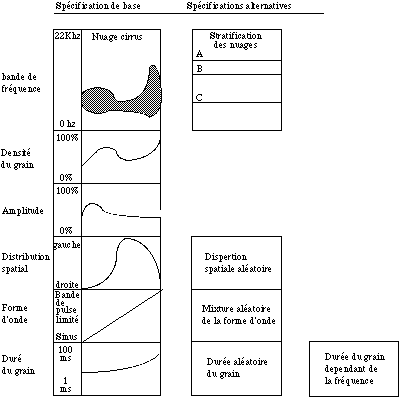
Figure 9.- Représentation graphique des paramètres d’un nuage. Plusieurs paramètres peuvent être spécifiés de plusieurs façons. (Roads, 1992).
Les différences principales avec le contrôle des paramètres développées en 1975 sont que Roads contemple maintenant la variation de la durée du grain, qu’il contrôle la largeur de bande de fréquence (bandwidth) du nuage avec un tendency mask [20] non linéaire, qu’il propose l’utilisation d’une enveloppe de distribution spatiale, la possibilité d’avoir une série de hauteurs fixes pour les grains (comme s’il s'agissait d’une harmonie granulaire), et la possibilité de changer la durée du grain en dépendant de la hauteur (des hautes fréquences utiliseraient des enveloppes courtes et des basses fréquences des enveloppes larges). Ce dernier point sera discuté plus loin, ainsi que les effets sonores produits par les différents paramètres; mais d’abord, faisons déjà une critique à la nouvelle proposition de Roads. Le seul grand défaut est qu’elle ne considère pas la variation de l’enveloppe du grain dans le temps. Comme je l’ai déjà mentionné dans la dernière section, la variation d’enveloppe peut enrichir le timbre des nuages granulaires, en particulier quand on combine le contrôle de ce paramètre avec la variation de la forme d’onde (voir le projet GiST dans le quatrième chapitre).
![]()
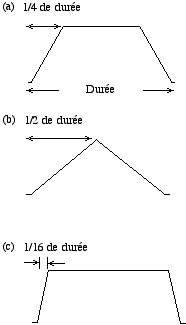
Barry Truax est le premier compositeur à avoir proposé et à avoir mis au point la possibilité de variation de l’enveloppe du grain dans le temps dans son implémentation de synthèse granulaire en temps réel avec le DMX-1000 (Truax, 1987, 1988). Ici, chaque grain a une enveloppe linéaire formé de trois parties. La durée de l'attaque et de la chute de l’enveloppe standard est de 1/4 de la durée du grain, mais d’autres proportions d’attaque et de chute sont disponibles qui vont de 1/2 à 1/16 de la durée du grain (Fig. 10). Dans ce système on peut donc varier d’une enveloppe à l’autre en temps réel, mais le seul désavantage est que la linéarité de la forme des enveloppes crée des effets de AM parfois excessifs, et des transitoires indésirables (Roads, 1991).
Le contrôle des paramètres pour les nuages granulaires va varier considérablement en dépendant des choix esthétiques des compositeurs ou des ingénieurs qui font les applications. On ne peut pas dire objectivement qu’un système de paramètres est meilleur qu’un autre, mais on peut dire que certains systèmes ont plus de potentiel sonore que d’autres. Les systèmes en temps réel auront certaines limitations (de mémoire RAM par exemple), que les autres systèmes n’auront pas, mais ces derniers demanderont par contre un temps de calcul parfois énorme. Le hardware et le choix du langage de programmation vont également affecter l’architecture de l'implémentation et par conséquent, le côté esthétique de la production de la synthèse. Je traiterai davantage les aspects esthétiques de l'implémentation des systèmes de synthèse granulaire dans la prochaine section, ainsi que dans le quatrième chapitre, ou l’on verra comment on peut utiliser plusieurs algorithmes pour contrôler les paramètres des nuages granulaires. Pour l’instant, on peut dire que dans les premières applications de AGS que Roads et Truax ont créé [21], on a utilisé le même type d’idées concernant les enveloppes et les tendency masks pour définir l'évolution de paramètres. Avant eux, seulement Xenakis avait eu des idées peut-être plus complexes du point de vue des algorithmes utilisés (voir chapitre 1), mais malheureusement, ces idées sont plutôt restées à l’état théorique, et on a très peu d'exemples de synthèse granulaire réalisées par lui.
A partir de la proposition de Roads, j’avais développé en 1993 un système de synthèse granulaire avec Csound et PatchWork [22] (Rocha Iturbide, 1994) où je contrôlais tous les paramètres en utilisant un tendency mask non linéaire construit par deux enveloppes qui varient de façon continue dans le temps, une pour les valeurs minimales, et l’autre pour les valeurs maximales. J’ai trouvé que le contrôle stochastique d'un nuage granulaire devenait beaucoup plus précis. Pourquoi Roads a-t-il utilisé un tendency mask avec deux enveloppes de ce type pour contrôler seulement l’évolution de la bande des fréquences?. Mon doute persiste. Peut être parce qu’il croyait que les autres paramètres n’avaient pas besoin d’un contrôle stochastique non linéaire. Dans tous les cas, je crois qu’en ayant un contrôle de ce genre pour tous les paramètres on gagne beaucoup du point de vue de la composition.
b) Effets paramétriques dans la synthèse granulaire asynchrone.
J’ai traité au début de ce chapitre les principaux effets sonores produits dans la synthèse QSGS et AGS. Examinons maintenant avec plus de détail les effets sonores de la synthèse AGS en partant des expériences de Roads et Truax, et confrontons-les avec les miens.
Comme on l’a déjà dit, les différents choix faits par l'ingénieur ou le compositeur au moment de construire un instrument de synthèse granulaire vont dépendre "d’une expérimentation musicale, de l’intuition et du goût" (Roads, 1992). Les expérimentations réalisées auront une approche empirique, dépendant aussi des buts artistiques, et parfois psychoacoustiques. Par rapport au dernier objectif, on a parlé du continuum entre la synthèse granulaire périodique et apériodique, spectrale et morphologique, et des étapes intermédiaires. L’avantage de la synthèse granulaire est que la perception peut changer dans une palette assez grande de phénomènes sonores, alors que des techniques de synthèse comme la FM ou la synthèse additive ont un champ d’action plus limité.
b.1) Effets de la durée du grain.
On a parlé dans le premier chapitre des premières bornes psychoacoustiques proposées pour la perception du quantum sonore par Gabor, Moles, Greens, etc, (entre 10 et 60 msecs). A partir de là, Roads avait proposé d’abord des durées de grain entre 10 et 20 msecs (Roads, 1975), et après entre 5 et 100 msecs (Roads, 1991). En réalité, on peut aller au-dessous et en-dessus de ces valeurs (de 1 msecs à 200 msecs ou plus). Il faut simplement prévoir les effets qui se produiront en prenant en compte si on a des grains périodiques ou apériodiques, mais en tenant compte aussi de la densité granulaire, car ces deux facteurs vont affecter nettement les effets de la durée du grain.
Pour des grains avec un délai périodique, J’ai abordé l’effet de modulation résultante AM, et j’ai dit que si on raccourcit la durée du grain, il y aura une largeur de bande plus large [23]. La formule pour déterminer la largeur totale de la bande de fréquence B est inversement proportionnelle à la durée du son D (Roads, 1991):
B = 1/Dg.
Quand on a un grain de 1 msec avec une fréquence de 500 Hz, le ratio entre la durée du grain et la période de sa fréquence P est inférieur à 1: Dg/Pg < 1 , c’est-à-dire, 0.001/0.002 < 1 . Dans ce cas, moins d’une période de la fréquence de 500 Hz est représenté, et donc, on a comme résultat des produits de modulation (Fig. 11). Normalement, il faudrait toujours tenir compte de ceci, et utiliser des fréquences plus aigues pour des grains plus petits. Dans ce cas il faudrait une fréquence minimale de 1000 Hz pour avoir au moins une période de la fréquence représentée (Fig. 12). Toutefois, il peut être souhaitable d’avoir ces produits "indésirables" de modulation pour créer des sons intéressants qui "tendent à générer une particulation du nuage dans laquelle une sensation de fréquence est toujours présente, mais brouillé par le bruit généré par les produits de modulation" (Roads, 1991). Malgré l'intérêt de cet effet sonore, les produits de modulation en rapport avec l’enveloppe du grain peuvent parfois créer de l'énergie transitoire qui s'étend au dessous et en-dessus du rang de la fréquence centrale, et l'énergie des basses fréquences peut créer des clicks semblables à ceux qui se produisent quand on coupe une onde à la moitié (au lieu de la couper au début) au moment de faire un montage sonore digital. Comme je l’ai déjà dit, pour atténuer ces effets on peut toujours utiliser un filtre passe-bande à la sortie du signal, centré sur la fréquence fondamentale de la période de la forme d’onde du grain.
Il n’existe guère de compositeurs à avoir fait des expériences avec des durées de grain au-dessous de 5 msecs, comme si l’on craignait de perdre complètement la qualité du grain et le contrôle sur les effets "indésirables"; mais dans le passé, il y avait aussi le fait de n’avoir pas de systèmes capables de générer des grains de cette taille, dû à des limitations de mémoire vive ou à des calculs trop longs. Plus petite sera le grain, il faudra un plus grand nombre de grains pour remplir le même espace de temps; pourtant, l’ordinateur a besoin de faire d’avantage de calculs. Prenons comme exemple le premier système de synthèse en temps réel développé par Truax où la durée de grain minimale a été restreint à 8 msecs (Truax, 1987 et 1988). Également, le délai entre chaque grain était limité dans certains systèmes, comme Max/FTS [24], aux messages de contrôle échangés entre les objets (un message chaque 64 échantillons); donc, avec un taux d'échantillonnage de 44100 Hz, on pouvait avoir un délai minimal limité à 1.44 msec (Eckel et Rocha Iturbide, 1995). Dans ce dernier cas, on ne pouvait pas avoir de grains périodiques de 1 msec [25].
Certains ingénieurs de son comme Norbert Schnell qui a travaillé à l’IRCAM récemment, se sont intéressés au micro-domaine de la durée du grain, et ils essaient actuellement de créer des systèmes de synthèse granulaire qui permettent de travailler dans ce domaine. Moi-même, en collaboration avec Gerhard Eckel, ai développé un système qui nous a permis de travailler avec des grains et des délais minuscules, même inférieurs à 1 msec (Eckel et Rocha Iturbide, 1995) [26], mais j’avoue que je ne m’étais pas intéressé jusqu’à présent à la création de sons avec des grains inférieurs à 5 msecs.
Quand on se réfère à la durée du grain, il faut revenir en arrière et reparler du concept du continuum spectro-morphologique (Smalley, 1985) et de la perception psychoacoustique. Selon Truax:
"La perception de la fréquence et du timbre dépendent de la durée d’un son. Avec des sons isolés, la durée nécessaire pour percevoir la hauteur est de 13 msec (Olson 1967) et le timbre émerge entièrement après 40-50 msec.....Le seuil de 50 msec est une ligne de division approximative entre les effets psychoacoustiques possibles. Autour de ce seuil et au-dessus de lui, les qualités de timbre du grain dominent, et au-dessous, la fusion de la proportion d’audio des fragments de l’onde du grain dominent" (Truax, 1988).
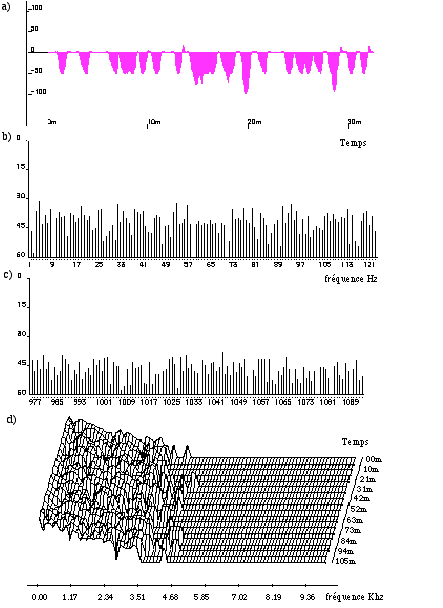
Figure 11.- AGS. Grains de 1 msec avec une fréquence de 500 Hz. a) La période est coupée à la moitié. b) et c) FFT du signal; L’énergie acoustique est bien répartie dans tout le domaine de fréquence. d) FFT du signal avec une évolution temporelle.
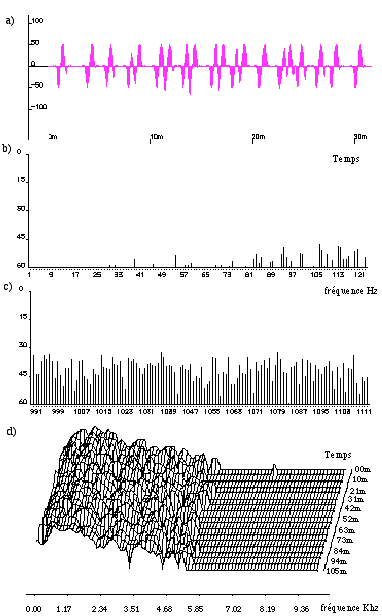
Figure 12.- AGS. Grains de 1 msec avec des fréquences aléatoires entre 1000 et 1500 Hz. a) La période est toujours entière. b) et c) FFT du signal; il y a peu d’énergie acoustique dans les fréquences graves et beaucoup dans les aiguës. d) FFT du signal avec évolution temporelle.
D'après mes expériences personnelles, ce seuil de perception de 50 msecs peut beaucoup varier par rapport à la densité (nombre de grains par seconde) et à la portée de la bande de fréquence, mais il est vrai que si on a une densité pas trop large et une portée de fréquence assez large, on peut commencer à écouter le grain comme une petite note à partir de 40-50 msec (c’est-à-dire, comme un son indépendant). Cependant, il ne faut jamais perdre de vue que toutes les paramètres de la synthèse granulaire son liés les uns aux autres, et qu’on ne peut parler de chaque paramètre de façon isolée. Si on a par exemple des grains de 100 msecs avec une fréquence fixe, une enveloppe sans attaque pointue, et un délai de 10 msecs entre chaque grain, on n'écoutera pas des notes séparées mais un continuum spectral, où l’on a comme résultat un effet de modulation bien connu appelé flanging [27].
Truax a définit deux types de continuums; l’un, entre la perception de fréquence et la perception de timbre, qui fonctionne si l’on écoute les grains avec des délais entre eux. Au moment où la densité augmente (même si les délais se rétrécissent), on commence à avoir un autre continuum qui se produit entre le magma généré par les effets de modulation issus des fréquences basses qui n’ont pas une période entière (entre 10 et 40 msecs), et le grain perçu comme entité complète et indépendante (à partir de 40 msecs). Ceci est le continuum entre le grain comme entité désintégrée et le grain comme entité intégrale. Dans le premier pôle, on perçoit le résultat de la combinaison des particules de grains, dans l’autre pôle on perçoit le grain comme événement isolé. Mais quand on se trouve entre les deux pôles, qu’écoute-t-on?. Voici encore le paradigme de la théorie quantique.
"La réalité comme on la connaît consiste en ondes (rapport) et en particules (individualité), de la même manière que la vie mentale de l’homme consiste en conscience immédiate (unité et intégration), et en calcul (pensée, structure). Un modèle adéquat de la nature de la conscience et de son rapport avec le cerveau doit prendre en considération les deux positions" (Zohar, 1990).
Les deux pôles se confondent dans le continuum de la synthèse granulaire, et la plupart du temps il est difficile de les séparer, comme il serait difficile de dire à quel moment on a une conscience immédiate de quelque chose, ou à quel moment on réfléchit d’une façon structurée pour parvenir à avoir cette conscience. D’autre part, on ne peut pas vraiment parler de deux pôles dans le continuum car en réalité il n’est pas linéaire; on peut toujours avoir des grains longs (des notes) sans une identité individuelle, comme je viens de le décrire (Fig. 13). Encore une fois on voit à quel point le continuum est complexe, surtout quand on utilise des techniques stochastiques où l’on ne peut pas savoir exactement quand la perception du grain indépendant deviendra une perception de l’ensemble crée par le mélange des grains. Truax parle d’une étape intermédiaire du continuum de la durée du grain où il y a un phénomène de ce type:
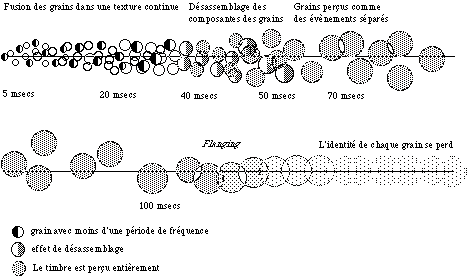
Figure 13.- Continuum non linéaire de la durée du grain.
"La moyenne de durée des grains, si l’on prend des petites valeurs de la portée de durée et des paramètres du délai, détermine la densité globale des événements. Si la durée du grain est bien inférieure au seuil de 50 msecs, le résultat est une fusion des grains dans une texture continue. Si les grains ont une durée bien supérieure à 50 msecs, ils sont perçus comme des événements séparés, selon si ils se déploient dans une portée de fréquence étroite ou large. Autour de 50 msecs, il y a un continuum entre la fusion de la proportion d’audio et les événements discrets - une espèce de désassemblage des composantes des grains" (Truax, 1988).
Roads a proposé une table qui décrit les effets de la durée du grain dans le continuum mais sans tenir compte de la densité et de la largeur de bande du nuage granulaire (Fig. 14). MacKey a aussi étudié le continuum entre la hauteur et le timbre comme on a vu dans la section sur la synthèse QSGS. Il a trouvé une série d’effets de texture sonores différents, en manipulant surtout les paramètres de la densité et de la largeur de bande des nuages granulaires. On parlera davantage de ces études au moment d’examiner ces paramètres.

Figure 14.- Effets de la durée du grain selon Roads.
b.2) Effets de la forme d’onde.
L’avantage de la synthèse granulaire est que l’on peut avoir une forme d’onde différente pour chaque grain. De cette manière, on peut créer des textures de timbre qui évoluent dans le temps. Le fait que le mélange d’ondes se fasse au niveau du micro-signal et du micro-temps modifie complètement le concept de mixage des signaux sonores. Il n’en serait pas de même si l’on faisait une synthèse additive traditionnelle avec des oscillateurs périodiques sinusoïdaux (domaine du continu), qu’une synthèse additive avec des grains sinusoïdaux également, mais dans le domaine du discontinu. On aura les mêmes fréquences spectrales de base dans les deux, mais dans la synthèse additive granulaire [28] on aura des effets de modulation de phase, d’amplitude modulée, et une texture différente générée par la granulation et la discontinuité (Figure 15).

Figure 15.- a) Synthèse additive traditionnelle b) Synthèse additive granulaire. Les discontinuités, les chevauchements des grains, et une possible utilisation d’un BW de 10 Hz pour chaque bande spectrale font que le spectre de b) soit différent de celui de a).
Les formes d’onde les plus simples sont synthétiques. Roads a proposé une possible évolution entre une onde sinus et une onde avec une bande limitée (bandlimited waveform) faite à partir de l’addition de n ondes sinus, où n est une implémentation spécifique de nombre (Roads, 1991). Curtis Roads a fait des essais en additionnant de 1 à 10 harmoniques naturels pour créer les formes d’ondes. A partir de cette idée, j’ai fait également des expériences en utilisant le logiciel PatchWork (Laurson, Rueda, Duthen, 1993) pour créer un score pour Csound (Vercoe, 1986). Ainsi, on peut faire une évolution de timbre qui va d’une onde sinus pure à une onde qui a 10 harmoniques (Figure 16a). Roads appelle transchrome le résultat d’une évolution de ce type. Il distingue les différentes couleurs des nuages granulaires. La couleur la plus simple serait le monochrome, où il y a un seul type de forme d’onde; ensuite, ce serait le polychrome, ou l’on peut avoir en même temps deux ou plusieurs formes d’ondes, et finalement le transchrome, qui est semblable au polychrome, sauf qu’ici il y a un processus évolutif. Le mélange de grains dans le deux couleurs complexes (transchrome et polychrome ) se fait par des opérations aléatoires qui dépendent du plan du système de contrôle. Avec mon système Csound PatchWork j’ai fait des nuages transchromes où il y a une évolution statistique avec un tendency mask contrôlé par deux enveloppes. Il y a une lecture stochastique des dix tables d’onde à partir de l'évolution des valeurs des deux enveloppes. Supposons que l’enveloppe inférieure a comme valeurs 1 2 3 4 5 6 7 8, et l’enveloppe supérieure a comme valeurs 3 4 5 6 7 8 9 10. Au début de la synthèse, on aura un mélange aléatoire entre les trois premières tables d’onde, ensuite entre la deuxième, la troisième et la quatrième, et ainsi de suite jusqu’à parvenir à un mélange entre la huitième, la neuvième et la dixième table. Comme les tables d’ondes sont de plus en plus complexes (il y a plus d'harmoniques à chaque fois ), on a une évolution de timbre transchrome qui va des ondes simples aux ondes complexes (fig. 16b). Ici, j’ai montré un processus simple et linéaire, mais avec deux enveloppes, on peut mettre en oeuvre des processus non linéaires plus complexes.

Figure 16a.- Grains de 20 msecs à 400 Hz avec augmentation de composantes spectrales. a) 1 harmonique. b) 3 harmoniques. c) 6 harmoniques. d) 9 harmoniques.
La micro-structure du grain peut être plus compliquée quand on utilise une forme d’onde qui varie dans le temps comme un signal généré par la méthode de fréquence modulée ou par d’autres techniques non linéaires (Jones et Parks, 1988). Le seul problème est que puisque le grain est parfois très court, on peut avoir comme résultat des textures distordues ou bruiteux, à moins que l’on contrôle soigneusement le taux de modulation (Roads, 1991). Barry Truax est un des premiers compositeurs à concevoir une synthèse granulaire en utilisant des grains avec fréquence modulée (Truax, 1986b). Il contrôlait d’une façon aléatoire le taux et la portée de l’index de modulation, et en conséquence, le potentiel des évolutions de timbre était très étendu (Fig. 17). Jones et Parks ont proposé des grains avec une fréquence modulée linéaire en utilisant une enveloppe gaussienne et deux multiplications complexes par échantillon (Jones et Parks, 1987).
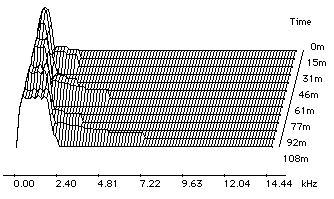
Figure 16b.- Enveloppe spectrale d’un son granulaire Transchrome qui
évolue entre une onde sinusoïdale et une onde avec 10 harmoniques.
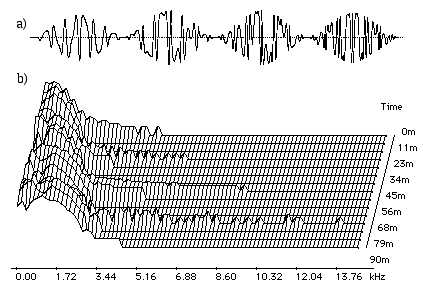
Figure 17.- Évolution spectrale de l’index de modulation des grains FM. Fréquence du carrier, 400 Hz. Fréquence du modulateur, 327 Hz. a) Grains de 20 msecs avec index de modulation croissant (1, 2, 3, 4). b) Enveloppe spectrale transchrome des 4 grains.
La forme d’onde peut aussi être extraite d’un son échantillonné. J’ai déjà un peu parlé de la Granulation de sons échantillonnés (granular sampling), et j’en parlerai davantage dans ce chapitre, dans la section sur la granulation temporelle avec des sons échantillonnés. La seule dernière remarque à faire par rapport à la forme d’onde est qu’il faut toujours tenir en compte que l’on peut avoir un effet de repliement si on utilise des ondes complexes avec des fréquences plus basses que le dessous de la moitié du taux d'échantillonnage. L’effet de repliement fait que les composantes qui dépassent cette limite se reflètent dans la partie grave du spectre. Roads conseille l’utilisation des ondes avec une fréquence fondamentale entre 11.025 et 14 Khz, en dépendant du taux d'échantillonnage.
b.3) Effets de bande de fréquence.
"Dans la synthèse granulaire AGS, la fréquence fondamentale de l’onde du grain est déterminée par les paramètres de bande. Les grains sont généralement éparpillés d’une façon aléatoire entre les limites supérieures et les limites inférieures de la bande. Ceci crée des effets de timbre et d’harmonie complexes quand la bande est au-delà de plusieurs demitons et quand la densité est large" (Roads, 1991).
Dès 1975, Roads conçoit l’utilisation d’une bande de fréquence variable dans la synthèse granulaire asynchrone pour déterminer la fréquence des grains et la forme des nuages granulaires [29]. Avant lui, Xenakis avait conçu une dispersion des grains stochastique par rapport à leur fréquence, intensité et densité, associées avec un système de trames beaucoup plus complexe (voir premier chapitre), où chaque trame était construite par de rectangles des grains ÆF, ÆG. Dans ce système, les grains des rectangles étaient répartis au hasard, suivant des lois stochastiques particulières (Xenakis, 1971). L'évolution de la bande de fréquence serait déterminée ici par la succession d’une série des trames dans le temps. On parlera davantage de ces trames et des algorithmes mathématiques utilisés par Xenakis dans le sixième chapitre.
Malgré la simplicité du système stochastique proposé par Roads, son avantage est la réduction d'information pour marquer l'évolution de la bande de fréquence avec seulement quatre valeurs pour établir l'évolution d’une bande variable linéaire (valeur de départ et d’arrivée de l’enveloppe inférieure, et valeur de départe et d’arrivée de l’enveloppe supérieure) (Fig. 18 d). Néanmoins, il est toujours plus intéressant de créer des bandes qui varient d’une façon continue dans le temps et qui utilisent deux enveloppes avec plusieurs valeurs chaque une, car ici la forme du nuage granulaire est plus intéressante (figure 18 e). La bande la plus simple proposée par Roads aurait seulement deux valeurs fixes, l’une pour l’enveloppe inférieure et l’autre pour l’enveloppe supérieure (Fig. 18 c). A mon avis, cette bande ne sert pas à grande chose pour créer des sons intéressants à utiliser dans la composition électroacoustique, puisqu’on aura toujours comme résultat des paquets granulaires statiques et fixes [30].
Je viens de décrire les bandes de fréquence où la distribution aléatoire des grains dépend des limites inférieures et supérieures des bandes. Roads a crée le terme de cumulus pour appeler ces bandes. Mais il ne s’est pas arrêté ici; il a aussi proposé des bandes de fréquence qui sont limités à une série de fréquences spécifiques (Roads, 1991) (Fig. 18 a et f). Dans ses premières expériences (1975), Roads n’a pas contemplé cette possibilité, probablement parce qu’il partait de la proposition stochastique de Xenakis. Ce dernier s’intéressait à la liberté et la flexibilité des grains dans l’espace temps-fréquence, et donc, il ne pouvait pas restreindre les grains à des fréquences spécifiques, puisque cela signifiait un retour à une conception spectrale et verticale de la synthèse. Xenakis est allé à l'extrême du domaine temporel et il a développé des idées qui ont servi à pratiquer la synthèse d’une façon entièrement nouvelle, mais après lui, et après les premières expériences de Roads dans les années soixante-dix, et de Truax dans les années quatre-vingt, il a tout de même fallu contempler la possibilité de créer des nuages granulaires avec des fréquences précises qui pourraient évoluer dans le temps (Fig. 15 b).
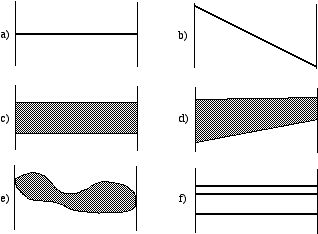
Figure 18.- Différentes spécifications de bande pour un nuage selon Roads. a) Bande d'une fréquence. b) Bande d'un glissando. c) Bande large constante. d) Bande large variable. e) Bande variable non linéaire. f) Nuage Stratus (harmonique) avec différentes bandes de fréquence (Roads 1992).
Dans sa nouvelle proposition des bandes de fréquences avec des fréquences spécifiques qu’il appelle stratus (1991), Roads suggère plusieurs possibilités: une bande avec une seule fréquence (Fig. 18 a), et une bande constituée par plusieurs fréquences fixes (Fig. 18 f). Il suggère aussi la possibilité d’avoir une bande avec une fréquence qui a un effet de glissando (Fig. 18 b). Avec cette proposition de conglomérats granulaires avec des fréquences structurées en stratus, on peut finalement envisager et imaginer des nuages granulaires harmoniques ou spectraux. Il me paraît étonnant que Roads ne propose pas la possible évolution des fréquences et donc des harmonies granulaires, comme je l’ai déjà suggéré dans ce chapitre (voir Fig. 15 b). Il est très facile d’imaginer une évolution de fréquences semblable à celle de la synthèse additive avec des ondes sinusoïdales, mais en utilisant des grains. On pourrait aussi varier d’une façon continue la bande de chaque fréquence et effectuer des processus entre le domaine spectral et le domaine de la texture et de la masse sonore où l’on ne perçoit plus clairement les fréquences qui se trouvent à l’intérieur du nuage granulaire (Fig. 19).

![]()
Dans la conception de bandes de fréquence cumulus on a beaucoup fait et beaucoup expérimenté, autant dans le domaine de la composition électroacoustique que dans le domaine de la psychoacoustique. La conception de bandes stratus a été beaucoup moins développée.
Il me semble qu'il ne faut pas séparer les deux domaines de bandes, car il y a la possibilité de aller de l’un à l’autre dans un continuum, comme je viens de le suggérer. Il est également important de tenir compte des effets psychoacoustiques qui peuvent être générés dans le continuum [31]. Truax est un des premiers compositeurs à avoir parlé du continuum dans le domaine des bandes de fréquence (Fig. 20):
"Le premier axe psychoacoustique est celui du continuum entre la fréquence et le bruit. Un rang de fréquence étroite permet à notre système d'audition de percevoir la fréquence résultante, mais quand le rang va au-delà du 10% de la fréquence centrale, la sensation de fréquence disparaît et donne lieu à une impression de bruit de bande étroite. Avec des valeurs plus grandes on parvient a une bande de bruit large" (Truax, 1988).
![]()
![]()
Dans la section de la synthèse QSGS on a parlé des effets psychoacoustiques générés dans le continuum par rapport à la sensation de fréquence et celle des différentes textures granulaires. La densité des nuages granulaires et leur largeur de bande sont étroitement liés à ces effets. MacKey a décrit le "spectre d’impressions de stratification" qui sont générées dans le continuum en termes d'élargissement de bande et de densité:
"Un élargissement de bande avec un élargissement comparable de densité granulaire donne lieu à un spectre d’impressions de stratification qui a une portée entre une bande de bruit, des écartements de bande avec des contours inférieurs et supérieurs très proéminents mais sans qu’il soit possible percevoir des identités de fréquence dans le milieu, et des écartements de bande avec des contours inférieurs proéminents, des contours supérieurs pas très proéminents, et un certain contenu de fréquence identifiable dans le milieu de la largeur de bande" (MacKey, 1984).
L'importance du travail de MacKey est qu'il décrit soigneusement les effets de texture qui sont générés dans la synthèse granulaire AGS, et le rôle de notre perception par rapport à ces changements de texture. La "texture" est un phénomène auditif qui a commencé à être utilisé de façon consciente par les compositeurs de musique instrumentale dans les années cinquante et soixante. Xenakis et Ligeti sont deux des figures les plus importantes à avoir développé le domaine de la texture sonore. La synthèse granulaire est le premier type de synthèse où l’on puisse travailler en profondeur avec les effets sonores de la texture, et ce n’est pas par hasard que Xenakis a été le précurseur de cette technique [32], car il était déjà intéressé aux effets sonores de la texture dans le domaine instrumental et il cherchait un moyen électronique de recréer ces sons, avec la capacité de dépasser les possibilités techniques des instrumentistes.
La qualité fondamental de la texture dans la musique est qu'on la perçoit comme une image globale stable composée d'une multitude d’événements; elle ressemble à l'image visuelle d'une carpette produite par un nombre large de crins et de fils (MacKey, 1984). Malgré l'existence d'une micro-structure de texture sonore, notre oreille nous invite à écouter une texture sonore de façon globale. Smalley a décrit ce phénomène:
"L'oreille éventuellement ne peut plus différencier les composantes séparées et doit alors se détourner vers la morphologie qui donne forme aux extensions élargies d'un mouvement structurel" (Smalley, 1986).
Cependant, notre ouïe peut se détourner à l’occasion d'une écoute globale de la micro-structure de la texture sonore quand il y a des inconsistances imprévisibles qui affectent la régularité de la texture. Il y se produit alors une interaction auditive entre l'aspect global ou externe de la texture, et l'aspect particulier ou interne de la micro-structure. L'oreille fonctionne d'une façon quantique, car elle doit changer spontanément d'une mode d’écoute à un autre. Mais si par hasard ces discontinuités et ces irrégularités de la micro-structure continuent à se répéter d'une façon homogène, elles s’intègrent à l'effet global externe de la texture, et on ne les écoute plus comme des éléments indépendants. La constance d'une bande de fréquence et de la densité des grains nous mettent sur une écoute globale, mais dans la synthèse granulaire asynchrone on peut faire varier les paramètres de façon radicale dans un instant donné, et alors on peut avoir une gamme de possibilités pour les effets de texture sonore. Néanmoins, il ne faut jamais perdre de vue que les effets de texture sonore complexes vont dépendre non seulement de la bande de fréquence et de la densité des grains, mais aussi de la durée des grains, de leur enveloppe, des formes d'onde et des délais entre les grains, etc, et des combinaisons de tous ces différents paramètres (Je développerai davantage les effets de texture complexes tout au long de cette étude). Si on a par exemple deux textures granulaires avec la même bande de fréquence, la même densité, et des grains avec la même durée, mais l’une des deux textures a occasionnellement des grains avec une durée plus longue, on aura une perception complètement différente de cette texture, alors que ce phénomène est généré par une seule variable (Figure 21). Toutefois, j’attribue une grande importance aux effets de texture sonore dans cette section parce que dans la synthèse granulaire les effets de texture vont être déterminés principalement par la dépendance entre les paramètres de bande de fréquence et de densité:
"Les effets de bande de fréquence et de densité sont en synergie. Les effets musicaux du paramètre de bande de fréquence changent en dépendant de la densité" (Roads, 1991).

Figure 21.- Textures granulaires selon MacKey.a) Texture homogène.
b) Texture homogène avec quelques grains d’une durée plus longue.
Des impressions générales de densité avec un taux de succession particulier et une bande de fréquence particulière peuvent être reproduites avec des bandes de fréquence et des taux de successions des grains supérieurs [33], ou avec bandes de fréquence plus étroites et des taux de succession inférieurs. Ceci représente un conservationisme de perception (MacKey, 1984). Cette remarque est très intéressante, parce qu'elle nous amène à la conclusion que la perception peut fonctionner plus au moins de la même façon à différentes échelles, en ce qui concerne l’augmentation ou la diminution simultanée des paramètres de bande de fréquence et de densité. Néanmoins, MacKey est conscient de que ceci ne se produit pas toujours exactement de cette manière, et que ce conservationisme de perception ne peut être tout le temps un guide efficace lorsqu’on étudie la perception des textures granulaires avec des buts musicaux.
Roads a établit une classification des effets de bande de fréquence avec des densités larges, qui commence avec des bandes étroites et conclut avec des bandes larges:
1.- Les bandes étroites avec des densités larges créent des flots avec une hauteur et un spectre formantique, comme dans la synthèse QSGS.
2.- Les bandes moyennes (des intervalles avec plusieurs semitons) et des densités larges créent des bruits colorés [34].
3.- Les bandes larges (une octave ou plus) et des densités larges créent des nuages sonores massifs.
Cette remarque est semblable à celle de Truax sur le continuum entre la fréquence et le bruit, mais ici Roads est plus spécifique par rapport aux effets de texture produits (voire figure 20). Pour l'instant, la conclusion à laquelle on parvient c'est qu’il est possible de créer différents effets sonores de texture en modifiant le paramètre de bande de fréquence et le paramètre de densité, mais on sait qu'il est toujours possible d'affecter la micro-structure de la texture en variant les autres paramètres. Je parlerai de toutes ces variantes dans cette étude, car le concept de texture sonore est très important pour la synthèse granulaire en général [35].
Avant de conclure avec la description des effets par rapport à la bande de fréquence et la densité, je voudrais faire une dernière remarque. Même s’il existe une espèce de conservationisme de perception quand on affecte les paramètres de bande de fréquence et de densité en proportion directe, ceci ne marche pas du tout quand on modifie l’échelle du temps. Imaginons par exemple une même bande de fréquence variable non linéaire [36] avec un son granulaire qui dure seulement un seconde, et avec un son granulaire qui dure 10 secondes. Dans le premier exemple, on aura une sensation auditive de la forme extérieure de la texture, ou comme dirait Smalley, une sensation du contour externe d'un geste. Dans le deuxième exemple, on aura une sensation auditive par rapport au comportement interne des composantes de la texture. Dans les deux cas, il s'agit d'une texture granulaire avec une densité proportionnelle et la même bande de fréquence, mais la perception des deux sons est complètement différente, due à leur différente longueur (Fig. 22 a et b). Il est intéressant de noter qu’il n'y a pas beaucoup des compositeurs électroacoustiques qui se soient intéressés à créer des sons granulaires très courts, avec des variations drastiques de bande de fréquence. Pour un son qui dure une seconde, changer la durée du grain, la forme d'onde, ou la densité, ne va pas trop modifier notre perception, mais le changement de la bande de fréquence va beaucoup faire varier notre perception, car on écoutera surtout la forme extérieure du son. Dans une seconde, il n’y a guère de temps pour se concentrer sur les composantes internes d’une texture; on peut seulement percevoir une couleur. Quand on pense à la synthèse QSGS et AGS, on imagine toujours de longs phénomènes de masse sonore qui varient plus ou moins lentement dans le temps, mais le domaine du micro-temps dans la synthèse granulaire pourrait être très intéressant. Ce domaine peut être contrôlé d'une manière plus fine quand on utilise des méthodes granulaires d'analyse-synthèse. Quand les sons granulés ont une bande de fréquence étroite, ils sont parfois semblables à certains sons instrumentaux de percussion et même à l’utilisation particulière d’un archer d’un violon sur ses cordes [37]. Je donnerait plus de détails sur des sons granulaires dans le domaine du micro-temps dans le troisième chapitre.
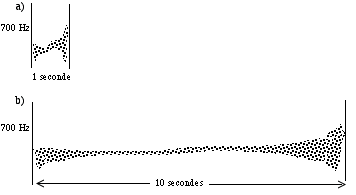
Figure 22.- Deux textures granulaires avec les mêmes paramètres de densité et une bande de fréquence semblable. Le son a) est perçu comme une note avec un transitoire drastique et une texture colorée. Les son b) est perçu comme une texture où on se concentre davantage sur les composantes internes et moins sur la forme externe.
b.4) Effets de densité.
La densité peut être définie comme le nombre de grains par seconde mais cette mesure devient invalide quand la durée des grains change au cours du nuage. En ce sens, il vaut mieux mesurer la proportion de grains par rapport au silence dans le nuage. Roads fait une classification de trois différents types de densités:
• Clairsemée: Plus de 50% de la durée du nuage est silence.
• Remplie: Le nuage est rempli par des grains sonores.
• Dense: Le nuage est rempli par un haut degré de chevauchement de grains.
Il est clair que si l’on précise 10 grains par seconde dans un programme de synthèse granulaire, on n’aura pas la même densité si l’on à des grains de 100 millièmes de seconde ou des grains de 10 millièmes de seconde. Si le délai est constant, dans le premier cas on aura un nuage rempli et dans le deuxième cas on aura un nuage clairsemé avec 90% de silence. Donc, la densité est directement proportionnelle à la durée du grain. Il faut aussi prendre en considération que les délais entre les grains dans la synthèse AGS sont plus ou moins variables, car on a un contrôle stochastique sur eux. Ceci peut créer des espaces vides entre les grains, et si on fait un changement de délais drastique entre eux, on aura comme résultat un nuage avec groupuscules de grains séparés par des régions de grains moins denses (Figure 23 a et b).
Pour être certain que l’on aura comme résultat auditif un nuage rempli, Roads suggère comme règle générale d’utiliser une densité par seconde égale à deux fois la durée du grain divisé entre 1 seconde: 2 * (Dg/1000 msecs). De cette manière, pour un grain de 10 msecs, il faudrait 200 grains par seconde pour remplir le nuage.

Figure 23.- Deux densités granulaires de 54 grains de 70 msecs par seconde.
a) Le délai entre les grains est régulier. b) Le délai entre les grains est variable.
La durée des délais entre les grains peut modifier notre perception de la densité, comme je viens de le suggérer (Figure 23). Un nuage avec des effets pointillistes est rempli de longs délais entre les grains, et donc, chaque grain est perçu comme un événement séparé. Roads propose aussi une formule pour créer ce type d’effets, où il faut avoir une densité par seconde égale à 0.5 multipliée par la durée de la seconde divisée entre 1 seconde:
0.5 * (Dg/1000 msecs).
Dans ce cas, pour un grain de 10 msecs il faut avoir 50 grains ou moins par seconde pour avoir un effet pointilliste. D’autre part, si on a des petites espaces vides entre les grains inférieurs à 50 msecs, on ne les entendra pas comme des silences, mais comme des fluctuations d’amplitude (Roads, 1991).
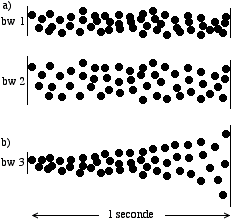
La valeur de la densité dépend aussi de la bande de fréquence [38]. Deux nuages granulaires avec des bandes de fréquence différentes mais avec la même quantité de grains par seconde, seront perçus comme deux densités différentes (Fig. 24 a). D’autre part, si on a la même densité pour tout un nuage, mais la bande de fréquence devient plus large, il y aura un décroissement de sa densité (Fig. 24 b). MacKey propose la création d’une unité de valeur avec laquelle on puisse mesurer la densité granulaire, telle que: Grains par seconde par tierce mineure, qui serait comparable à l’unité de valeur de Grammes par Centimètre Carré (MacKey, 1984). La proposition est fondé sur l’idée du conservationisme de perception, selon laquelle "les impressions de densité qui se suscitent à partir d’un taux de succession et une bande de fréquence particuliers, sont apparemment reproductibles avec des bandes de fréquence et des taux de succession supérieurs ou inférieurs" (MacKey, 1984) [39]. La seule contrainte est que cette unité serait valable seulement si on ne faisait pas varier la bande de fréquence du nuage granulaire, et si on ne dépassait pas le seuil maximum de 4000 Hz, ou le seuil minimum de 100 Hz.
![]()
Nous venons de voir comment une variation de la bande de fréquence peut affecter la perception d’une densité. Une variation de la durée du grain peut aussi altérer notre perception de la densité. Les effets psychoacoustiques résultants des deux nuages avec une même densité mais avec une durée de grain différente ne seront pas semblables. Le timbre va complètement changer, surtout quand on a des grains inférieures à 50 msecs dans un nuage et des grains supérieurs à 50 msecs dans l’autre. Avec le premier nuage on aura un fort effet de fusion, et avec le deuxième, un effet où l’on perçoit davantage les grains comme des événements séparés (voir section sur les effets de la durée du grain). Néanmoins, ceci dépendra aussi du degré de densité, de la bande de fréquence, et de la régularité de délais entre les grains.
Pour analyser les effets psychoacoustiques de la densité, on ne peut plus parler d’un paramètre de façon isolée, car tous les paramètres sont interdépendants; toutefois, si l’on crée des constantes, on peut parler d’un continuum des effets psychoacoustiques de densité. Roads et Truax ont essayé de décrire les effets sonores de ce continuum. MacKey les a étudiés plus en profondeur, et il a réussi à établir différents seuils de perception (MacKey, 1984). Avec 15 g/s (grains par seconde) on commence à avoir une disparition des structures rythmiques possibles. Avec une succession de grains chaque fois plus rapide, on perd la sensation d’une accélération du tempo, et on la perçoit plutôt comme une augmentation d’intensité du flot des grains. Quand on parvient à 25 g/s, on perd la sensation d’un ordre relatif entre les grains, et les limites supérieure et inférieure de la bande de fréquence commencent à être clairement perçues . En même temps, il est de plus en plus difficile d’identifier les fréquences au milieu du flot. Éventuellement, les fréquences commencent à être brouillées et deviennent un bruit statique; à ce moment-là, on perçoit seulement la fréquence des limites inférieure et supérieure de la bande de fréquence, mais notre audition change de mise au point de façon constante à cause des irrégularités du flot granulaire. A 50 g/s on a une "bande de texture" plus constante qui ressemble de plus en plus à un grouillement granulaire. Ici, il n’y a plus de perception des fréquences composantes internes de la texture, et la seule sensation de fréquence est donnée par les limites supérieure et inférieure de la bande de fréquence. Quand les textures deviennent beaucoup plus denses, on ne peut plus percevoir un espace apparent entre les grains et on perçoit une masse sonore. Finalement, quand on dépasse les 100 g/s on perçoit l’augmentation de densité comme une augmentation de volume et de distorsion de la masse sonore, qui semble occuper un espace plus grand. Ceci est un effet qui ressemble à certains types de réverbération. Truax décrit ce phénomène de la façon suivante:
"Pour expliquer la perception d’augmentation de volume dans le son, on peut revenir au concept de gestalt de volume et le définir comme "la magnitude perçue du son", qui tend à augmenter avec la richesse spectrale (ou résonance), la réverbération, la durée, et l’intensité" [40] (Truax, 1994).
Tout n’a pas été dit au sujet des effets psychoacoustiques de la densité; ceci est un domaine très riche et très vaste. Des compositeurs comme Ligeti et Xenakis ont beaucoup développé l’idée de densité dans leur musique instrumentale (Atmosphères et Lontano de Ligeti, et Pithoprakta et Metastasis de Xenakis par exemple). La synthèse granulaire nous permet d’expérimenter davantage avec la densité, car on n’a pas besoin de grands ensembles d’instrumentistes pour trouver de nouveaux effets sonores. Ces effets composés de différentes textures sonores ont été étudiés en rapport à notre perception par des chercheurs tels qu’Erickson (1975), McAdams et Bergman (1979), et MacKey (1984), mais il y a encore beaucoup à dire et à faire par rapport à ce paramètre. Je traiterait davantage le domaine de la densité tout au long de cette étude.
b.5) Distribution dans l’espace.
"Les caractéristiques distinctives de la synthèse granulaire sont agrandies par la distribution spatiale dans plusieurs canaux. Une texture granulaire est articulée par l’éparpillement des grains individuels dans différentes locations spatiales" (Roads, 1991).
La synthèse granulaire asynchrone peut créer des sons semblables à ceux qui se produisent dans l’environnement [41] . La qualité spatiale de ces sons fait partie essentielle de leur complexité, surtout parce qu’on contrôle les grains d’une façon stochastique. Quand on a des nuages granulaires très denses (ceci est équivalent aux masses sonores) on est tenté d’effectuer une spatialisation, car elles ont souvent un caractère statique.
L’idée de masses sonores complexes qui se déplacent dans l’espace appartient à une pensée musicale contemporaine qui n’a pas encore été entièrement développée, à cause de la difficulté d’écrire des milliers de notes et de disposer de centaines d’instrumentistes pour réaliser ces expériences. Edgar Varèse a été le premier compositeur à proposer l’appui d’instruments électroniques pour pouvoir développer cette idée:
"Quand de nouveaux instruments me permettront d’écrire de la musique comme je la conçois, ils prendront la place du contrepoint linéaire, et le mouvement des masses sonores et des plans qui changent seront clairement perçus. Quand ces masses sonores feront collision, on aura des phénomènes de pénétration et de répulsion. Certaines transmutations qui prennent place dans certains plans seront projetées dans d’autre plans, avec des déplacements de vitesse et d’angles divers. Il n’y aura plus la vieille conception de mélodie et de corrélation des mélodies. L’oeuvre entière sera une mélodie total. L’oeuvre entière coulera comme une rivière" (Varèse, 1936).
Les phénomènes sonores imaginés par Varèse [42] pourraient être recrées par la synthèse granulaire, car c’est une technique puissante qui nous permet d’expérimenter avec la spatialisation des masses sonores complexes sans avoir besoin de décrire chacun des milliers d’événements sonores en détail, elle nous permet aussi de gérer ces événements en utilisant des contrôles stochastiques qui peuvent être assez sophistiqués.
Roads propose deux façons différentes de spatialiser les grains: soit avec une seule enveloppe qui fait un paning à travers n canaux, soit avec une dispersion de grains aléatoire entre n chenaux. La première proposition n’est pas très avantageuse car on peut facilement reproduire cet effet à l’aide d’une table de mixage, mais elle devient plus profitable quand on a plusieurs voix et la possibilité de créer une enveloppe de spatialisation pour chaque voix (Fig. 25), ce qui nous éviterait de devoir enregistrer plusieurs pistes pour les spatialiser ensuite. La deuxième proposition est plus intéressante, car la spatialisation de chaque grain est indépendante, et donc, on peut avoir différents jeux statistiques où les grains sont éparpillés dans plusieurs zones de l’espace, et en outre, le constant mouvement aléatoire de chaque grain nous donne une sensation de quelque chose de vivant et d’organique. J’ai beaucoup travaillé avec cet effet en utilisant deux canaux et des délais rapides entre les grains, et malgré la limitation de la stéréo, on parvient à avoir une impression d’un espace tridimensionnel étendu. Avec un tendency mask non linéaire variable, la spatialisation devient encore plus riche, car on a deux enveloppes qui se meuvent dans le temps (Fig. 26).
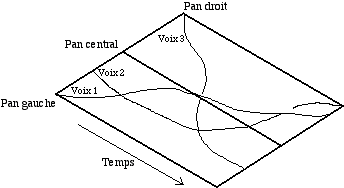
![]()
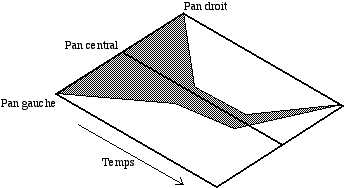
![]()
La particularité de la synthèse granulaire asynchrone, est que même sans spatialisation, on peut avoir divers effets sonores de mouvement grâce au déplacement des composantes internes des textures granulaires générées par la variation des différents paramètres (bande de fréquence, densité, durée du grain, etc) [43]. Smalley a décrit en détail les différents effets psychoacoustiques produits par le mouvement interne des textures spectrales (Smalley, 1986). La diversité de ces effets et leur combinaison est une source inépuisable pour le compositeur de musique électroacoustique, et une étude en profondeur serait recommandable pour le compositeur qui souhaiterait les recréer en utilisant la synthèse granulaire asynchrone [44].
A partir de ce qu’on a dit sur la synthèse AGS, on peut facilement imaginer plusieurs nuages avec différents types de mouvement interne, par exemple, un nuage avec des composantes se comportant comme un groupe cohérent (floked motion), un nuage avec plusieurs mouvements concurrents qui coulent (stream motion), et un nuage où les composantes se comportent de façon désordonnée (contorted motion), où ils ne peuvent être perçus comme un groupe d’éléments homogène qui se déplace (flocking), ni comme des flots qui coulent (streaming)[45]. Pour différentier d’une manière auditive ces différentes nuages, on pourrait avoir un timbre différent pour les grains de chacun (avec une forme d’onde différente), mais en outre, on pourrait aussi les spatialiser de façon différente. On aurait comme résultat deux types de mouvements, l’un correspondant au mouvement interne des composantes des nuages, et un autre correspondant au mouvement des nuages dans l’espace. Mais on aurait aussi l’interaction complexe des différents nuages (Fig. 27). On peut voir donc clairement le potentiel de la synthèse granulaire au niveau du mouvement des masses sonores et de leur spatialisation[46].
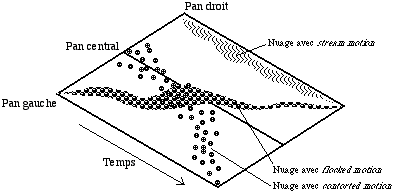
Figure 27.- Spatialisation de trois nuages granulaires, chacun avec une forme d’onde différente et avec un mouvement interne des grains différent.
A partir des études psychoacoustiques, on a déterminé que la perception spatiale de la position d’un grain ou d’une série de grains dépend des propriétés physiques du signal et du phénomène de localization blur qui est introduit par le système d’audition (Blauert, 1983). Cet effet crée une image auditive qui se propage à un certain degré dans l’espace à partir du point central de la localisation de la source sonore. Boerger a fait un étude approfondie des propriétés spatiales des grains gaussiens (Boerger, 1965), mais il me semble que cette information est plus importante pour le scientifique que pour le compositeur de musique électroacoustique, et donc, je ne l’analyserai pas.
b.6) Effets de l’amplitude.
J’ai très peu parlé des effets d’amplitude des grains dans la synthèse AGS. Curtis Roads a proposé un contrôle d’amplitude avec une seule enveloppe, c’est-à-dire, un incrément ou un décroissement du dB d’un nuage granulaire. Ceci ne modifie pas beaucoup les caractéristiques sonores d’un nuage, et si on veut créer des effets de fade-in et fade-out on pourrait toujours le faire dans une deuxième étape avec un éditeur digital d’audio. Par contre, le contrôle stochastique de l’amplitude de chaque grain est beaucoup plus intéressant, car il contribue à l’augmentation d’une sensation de volume tridimensionnel du nuage, qui peut aussi changer dans le temps. Un contrôle de ce type est facilement accompli par l’utilisation d’un tendency mask avec deux enveloppes (Fig. 28).
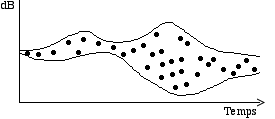
Figure 28.- Tendency mask pour le paramètre d’amplitude de chaque grain.
Xenakis a été très conscient de l’importance d’un contrôle stochastique pour l’amplitude de chaque grain, et c’est pour cela qu’il a défini le grain sonore élémentaire comme un produit de la fréquence et de l’intensité, où ces deux facteurs sont des ensembles indépendants (Xenakis, 1971). Xenakis définit l’ensemble global de grains dans un moment précis du temps dans une trame, grâce à l’utilisation d’une matrice de coordonnés F et G, où chaque grain peut avoir des valeurs d’intensité et de fréquence différentes avec l’appui des opérations de probabilité. Si on utilise une série de trames, on aura alors une évolution des grains dans le temps où leurs intensités et leurs fréquences vont changer d’une façon complexe (Voir chapitre 1).
Xenakis ne se réfère pas spécifiquement aux effets d’amplitude, mais au résultat global des variations de tous les paramètres (fréquence, amplitude, densité), toutefois, il a traité le paramètre de l’amplitude des grains au même niveau que la fréquence, car il était conscient des divers effets sonores possibles occasionnés par la variation de ce paramètre, surtout dans le domaine du timbre [47]. Le "discours sonore" de Xenakis est basé sur une perpétuelle fluctuation de l’entropie des grains, sous toutes ses formes. Son intérêt est centré sur des notions pures structurelles des transitions entre états d’ordre et de désordre, mais aussi sur les résultantes de la perception. Néanmoins, il n’a pas pu analyser en profondeur les effets psychoacoustiques résultants car il n’a guère fait d’expériences pratiques.
4.- Granulation temporelle des sons échantillonnés.
Selon Roads, la granulation des sons échantillonnés est une des techniques de synthèse les plus puissantes offertes par la représentation granulaire d’un signal. On peut trouver les origines de cette méthode avec l’apparition du granulateur sonore de Gabor basé sur un système d'enregistrement optique adapté à un projecteur de cinéma de 16-mm (Gabor, 1946) (Voir chapitre 1). Plus tard, Barry Truax a réalisé une application importante avec le processeur digital de signal DMX-1000 contrôlé par un PDP Micro 11 (Truax, 1987) [48]. Truax a été peut-être le premier à développer cette méthode en profondeur, particulièrement dans le domaine de la composition électroacoustique, et ceci grâce au fait d’avoir créé un système en temps réel avec lequel il était possible de réaliser de meilleures expériences.
a) Les différentes méthodes.
Roads définit trois différents types d’approximations dans la granulation temporelle:
1.- Effets changeants de temps/taux.
2.- Granulation temporelle en temps réel d’un son alimenté à l’entrée.
3.- Granulation d’un ou de plusieurs fichiers sonores gardés dans la mémoire et exécution de leurs grains de façon asynchrone.
Nous allons analyser ces trois approximations de Roads en faisant une description détaillée, à partir de nos expériences, et à partir des expériences d’autres compositeurs (notamment de Barry Truax). D’autre part, grâce à mes expériences pratiques et suite à mes conclusions, je me permets d’ajouter une quatrième approximation:
4.- Synthèse croisée entre deux fichiers sonores par granulation.
a.1) Effets changeants de temps/taux par granulation.
Avec cette méthode, la durée d’un son peut être étirée ou raccourcie pendant que sa hauteur reste invariable. On peut dans l’autre sens altérer la hauteur du son pendant que sa durée reste invariable. Ces deux effets sonores peuvent être accomplis par l’utilisation de diverses techniques d’analyse-synthèse (Vocodeur de phase, analyse-synthèse par ondelettes, Linear predictive coding, etc), mais l’avantage de cette méthode est qu’on a un contrôle souple du domaine temporel (par exemple, on peut avoir une lecture stochastique du son échantillonné), qu’on peut facilement réaliser une application en temps réel sans avoir besoin d’une grande puissance de calcul (vitesse de l’ordinateur), et que le résultat peut avoir différentes qualités de texture sonore (granulosité et volume). L’inconvénient principal est un manque de contrôle sur la phase des grains, et donc, des effets résultants de modulation, mais certains chercheurs ont découvert certaines techniques qui diminuent ces effets.
La technique pour changer la durée du son sans modifier sa fréquence est simple. Pour étirer un son de 200% il faut lire chaque grain deux fois, et pour raccourcir le son de 50% il faut lire un grain, ignorer le suivant, lire un autre grain, ignorer le suivant, et ainsi de suite. Pour changer la hauteur d’une octave sans modifier la durée du son, il faudrait simplement étirer d’abord le son d’un 200% et ensuite doubler le taux d’échantillonnage pour changer la hauteur. Dans ce cas-là, l’étirement précédent va compenser le changement du taux d’échantillonnage qui va raccourcir le son de moitié. On a déjà vu dans le premier chapitre comment Gabor avait effectué dès 1946 des granulations temporelles de ce type avec son granulateur sonore analogique (voir chapitre 1).
La première implémentation digitale de granulation temporelle a été effectuée à l’Université d’Illinois par Otis, Grossmann et Cuomo (1968), mais avec certains problèmes sonores dus à l’absence d’enveloppes. Le problème était que le début et la fin de la forme d’onde ne concordaient pas avec d’autres formes d’onde échantillonnées; on avait donc des discontinuités qui créaient des clicks sonores. Jones et Parks (1988) ont réussi à obtenir une reconstruction du signal sonore plus lisse grâce à l’utilisation d’une fonction fenêtre pour chaque grain et au chevauchement des fenêtres, mais ils ont trouvé des problèmes de désynchronisation de phase qui créaient un effet de beating (phénomène sonore du battement). Ils ont résolu ce problème avec un chevauchement de fenêtres toujours en phase, avec un rajustement de la position initiale de chaque fenêtre effectué par un algorithme (Jones et Parks, 1988). Lent (1989), a perfectionné cette technique par une détection de la fréquence du son original afin de déterminer la durée et l’espace des fenêtres Hanning utilisées pour la compression et l’expansion. La technique de Jones et Parks sera discuté dans le troisième chapitre sur "La représentation granulaire dans les techniques d’analyse-synthèse", car elle appartient à ce groupe.
a.2) Granulation temporelle en temps réel d’un son alimenté à l’entrée.
La granulation temporelle d’un son continu peut être effectuée avec un processeur digital de signal de haute vitesse exécutant une ligne de délai ou fenêtre qui se déplace pour fournir plusieurs grains. L’effet de granulation temporelle enrichit le son de l’entrée avec les produits spectraux de la fenêtre de granulation, et par la mixture du son original et le son affecté par un délai. Le but est de créer une distorsion du son d’entrée tout en gardant un certain contrôle (Roads, 1991).
Truax a effectué plusieurs expériences où le taux de lecture du son est diversifié par la vitesse changeante du déplacement du processeur à travers le son. Le son peut être ralenti par la lecture répétée d’un échantillon avant d’effectuer un pas en avance (Fig. 29). Truax définit le taux de changement temporel comme un ratio off msecs/on msecs. Un ratio de 0:1 correspond à une vitesse normale car il n’y a pas de temps off, et un ratio de 99:1 correspond à une répétition du même échantillon pendant 99 msecs avant que le processeur n’avance de 1 msec. Dans ce cas-là, on dilate le son par 100 (soit 10000%). Si l’on avait un son d’une durée de 3 secondes, on effectuerait une dilatation de 3 * 100, c’est-à-dire, de 300 secondes (soit 5 minutes).
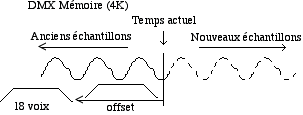
![]()
Plus on dilate un son, plus on découvre ses micro-caractéristiques spectrales. Ceci constitue l’intérêt principal de Truax, c’est-à-dire, l’exploration du micro-domaine sonore. C’est comme si l’on avait une lentille qui nous permettait de nous rapprocher des caractéristiques voilées du son. Truax a fait une analogie intéressante concernant la théorie de l’incertitude de Heisenberg. Il a trouvé qu’il y a un rapport de perception inverse entre l’écoute d’un son tel qu’il est, et l’écoute du son dilaté:
"Plus un son est dilaté, moins on est conscient de son enveloppe temporelle et plus on découvre ses caractéristiques dans le domaine du timbre. Ironiquement, avec une dilatation extrême dans le temps on peut expérimenter de manière psychoacoustique l’addition des composantes spectrales du son, comme s’il s’agissait d’une analyse de Fourier" (Truax, 1993).
On a parlé de l’effet de la largeur de la fenêtre et de la théorie de l’incertitude de Heisenberg. Plus courte est une fenêtre, plus le domaine de la fréquence est en expansion; donc, la largeur de bande augmente et le grain devient plus bruiteux. L’analogie de Truax est semblable mais dans le macro-domaine; plus courte est le son (si on effectue une compression de notre son originel de 3 secondes par exemple), moins on est conscient de ses caractéristiques de timbre et plus on l’est de son enveloppe dans le temps; avec une dilatation, on est plus conscient des caractéristiques spectrales et on l’est moins de l’enveloppe temporelle. Cette idée avait déjà été formulé par Smalley avec sa théorie sur la spectro-morphologie du son (voir section sur la synthèse QSGS).
La technique d’étirement de Truax est très semblable à celle de Jones et Parks (1988), mais il y a une grande différence entre les deux, Truax utilise jusqu’à 18 grains de façon simultanée, chacun avec des caractéristiques indépendantes, qui donnent comme résultat global une sensation d’augmentation de la magnitude sonore. De plus, le système de Truax a deux modalités, on peut lire les grains toujours en arrière, et cet effet modifie le résultat spectral de l’échantillon de façon minimale, ou bien modifier la direction de lecture (en avant/en arrière) entre les états de on et off, opération qui produit une modulation de l’échantillon au niveau micro. Cette deuxième option va altérer la constitution spectrale du son original, mais Truax a pour but de produire des sons musicaux intéressants, et non de trouver une formule pour reproduire les caractéristiques spectrales du son sans altération. Pour ce dernier but, il faudrait plutôt utiliser un vocodeur de phase, et même dans ce cas, il serait impossible d’éviter certains effets de modulation quand on dilate un son trop largement.
A partir de ses expériences comme compositeur électroacoustique, Truax a découvert plusieurs phénomènes sonores issus du changement temporel d’un son. En première lieu, un effet sonore de magnitude augmentée, toutefois différente du simple effet de loudness [49]. Le deuxième phénomène est un effet sonore des résonances momentanées à caractère souvent vocal [50]. L’explication de cet effet est que les résonances momentanées sont normalement trop fugitives et ne se répètent pas de façon à être identifiées par notre oreille, mais elles deviennent audibles quand on a plusieurs couches des grains prolongées dans le temps (Truax, 1993).
La perception des phénomènes sonores décrits peut être mieux comprise par le concept gestalt de volume déjà exposé dans la section sur les effets du paramètre de la densité dans la synthèse AGS. Plusieurs chercheurs en psychoacoustique ont étudié ces phénomènes (Kryter, 1959 et Olson, 1967) [51]. La corrélation entre loudness et intensité spectrale est constamment expliquée dans les livres de musique électroacoustique et de production d’audio, mais la théorie est rapidement ignorée dans la pratique, probablement parce que ces théories ne sont pas très utiles pour le compositeur (Truax, 1993). Néanmoins, Truax a proposé un modèle de travail pour le concept de volume qui possède les dimensions suivantes: richesse spectrale, temps, et densité temporelle. L’expansion d’un son par granulation est une technique qui possède ces trois dimensions, la superposition de plusieurs grains contribue à l’augmentation de la richesse spectrale, la désynchronisation entre les différentes voix granulaires augmente la densité temporelle, et la durée prolongée du son (dilatation) contribue à l’écoute des résonances momentanées. Toutes ces paramètres vont être reliés à l’augmentation de volume.
Mon travail personnel avec le système de synthèse granulaire en temps réel de Truax m’a permis d’expérimenter avec la granulation des échantillons en utilisant le paramètre de changement temporel (Variable rate sample sound) [52]. L’avantage du temps réel est que l’on peut varier le taux de changement à la main, et créer ainsi des accélérations et des ralentissements. On peut aller du son original au son dilaté dans ses différents degrés, et jouer ainsi avec la perception. J’ai constaté que la superposition des voix enrichissait l’évolution du timbre, et donnait la possibilité de varier la densité (en additionnant et en réduisant les voix). En plus, Truax a crée la possibilité d’harmoniser l’échantillon d’origine, en transposant certaines voix par une modification de leur taux d’échantillonnage sans avoir une altération de la durée du grain (Fig. 30). Cette modalité est très intéressante, mais il faut faire attention en choisissant l’échantillon car s’il est trop complexe, on aura rapidement une masse spectrale trop dense. La dilatation du système de Truax en elle même, avec toutes ses modalités, est déjà un outil très puissant qui peut modifier la structure spectrale du son originel et le rendre plus riche, sans avoir nécessairement besoin de le transposer.
Le système de Truax a sûrement été le première à avoir la puissance du temps réel, et l’idée sur l’exploration du micro-domaine du son est une innovation sur la synthèse sonore. Néanmoins, une technique de ce type peut avoir certaines limitations. Par exemple, une préoccupation excessive sur les qualités internes du son par des dilatations excessifs peut donner un résultat trop statique. Le son en lui-même peut être très intéressant, mais dans le contexte d’une structuration musicale, que peut-on faire avec lui ensuite?. Les techniques de synthèse vont toujours influencer l’esthétique d’une composition électroacoustique, et il faut tenir ce facteur en compte avant de commencer à travailler avec un outil informatique. Je parlerai des aspects esthétiques de la synthèse granulaire en profondeur dans le dernier chapitre. Une autre limitation du système de Truax est un manque de tendency masks avec lesquels on pourrait contrôler avec finesse l’évolution des divers paramètres. Cependant, ce système est fait sur tout pour être joué comme un instrument, et cette approche est très intéressante. Le problème est que le compositeur a besoin alors d’un temps assez long pour maîtriser l’instrument. J’aborderai les questions de structuration des systèmes dans la dernière section de ce chapitre.
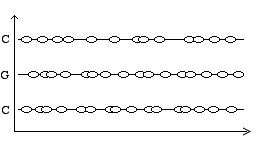
Figure 30.- Diagramme temps/fréquence d’un nuage harmonique avec la fondamental transposé à la quinte et à l’octave.
a.3) Granulation temporelle asynchrone.
Quand on fait une granulation temporelle d’un fichier sonore qui est gardé dans la mémoire, on peut extraire les grains de diverses manières: en séquence continue ou discontinue, en marche arrière, de façon aléatoire, etc. On peut également mélanger les grains de plusieurs fichiers sonores avec différentes caractéristiques spectrales pour créer un nuage de texture hybride (Roads, 1991) (Fig. 31), on peut avoir différentes notes d’un même instrument pour créer un nuage de texture monochrome harmonique [53], ou avoir différentes notes de différents instruments pour créer un nuage de texture hybride harmonique. D’autre part, on peut mélanger un nuage de texture hybride avec un nuage de texture monochrome [54] (Fig. 32), et finalement on peut créer des transitions statistiques entre deux nuages différents pour avoir des évolutions harmoniques (quand il s’agit des nuages harmoniques) (Fig. 33), des évolutions de texture (Fig. 31), et des évolutions entre harmonie et texture (ou vice-versa) (Fig. 19).
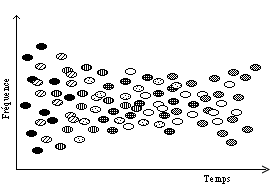
Figure 31.- Diagramme d’un nuage qui mélange grains de différents échantillons, avec une mixture qui évolue de façon statistique à travers le temps (Roads, 1991).
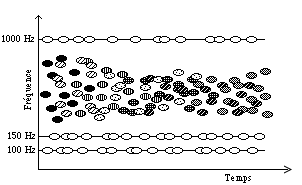
Figure 32.- Mélange d'un nuage de texture hybride avec un nuage de texture monochrome harmonique.
Il faut établir clairement la différence entre les divers types de nuages sonores que l’on peut créer avec la granulation temporelle asynchrone. Ceci dépend entièrement des sources sonores. Premièrement, on peut avoir des nuages avec des caractéristiques de fréquence, en utilisant des instruments musicaux ou des objets sonores qui ont une fréquence spécifique. Deuxièmement, on peut avoir des nuages avec un spectre riche où il existe une combinaison de fréquence et de bruit, par exemple, un instrument de percussion où l’attaque est bruyante mais la résonance a un spectre riche avec des composantes de fréquence nettes (un cymbale). On peut inclure ici les sons de certains animaux qui tantôt sont bruités, tantôt ont des fréquences claires (comme un chien qui aboie), la parole, etc. Troisièmement, on peut avoir des nuages où le spectre de la source sonore est très complexe et où l’on ne perçoit plus très clairement ses composantes, comme dans certains sons de la nature (la mer, le vent), certains sons de la ville (le bruit des voitures, des moteurs), et d’autres. Bien évidemment, il y a une gamme intermédiaire entre ces trois classes de sources sonores, mais nous essayons là de trouver des différences essentielles par rapport au continuum spectral de Smalley entre la note propre et le bruit (Fig. 6) [55]. Il est important de considérer que la deuxième classe possède des caractéristiques de la première et de la troisième classe, et que dans ce cas, la même source sonore pourrait présenter des transitions entre la note propre, un spectre riche, et le bruit (la voix parlé par exemple).
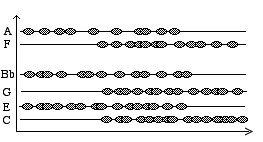
Figure 33.- Diagramme temps/fréquence d’une transition statistique entre deux nuages harmoniques (Roads, 1991).
Une variable importante dans la granulation temporelle asynchrone est que l’on peut transposer les fichiers sonores en changeant leur taux d’échantillonnage, soit de façon harmonique, soit de façon stochastique [56]. Avec toutes ces variables, on peut voir comment la granulation temporelle a des possibilités immenses dans le domaine du timbre. J’ai crée plusieurs schémas pour essayer de représenter cette complexité (Fig. 34 a, b et c).

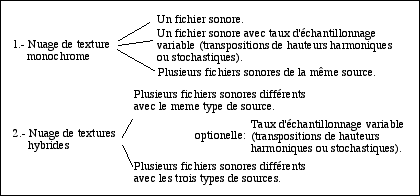
Figure 34b.- Nuages de texture monochrome et de texture hybride en rapport avec les différents types de sources sonores.

Figure 34c.- Différents types de transitions entre les différents types de nuages.
Pour maintenir les caractéristiques intrinsèques de la source sonore, il faut respecter une durée de grain minimale. Par exemple, pour des fichiers sonores de voix parlée, il faut avoir des durées de grain assez longues (entre 30 et 50 msecs) pour pouvoir identifier la source (Roads, 1991). Autrement, si on utilise des petits grains de 10 msecs ou moins, la source devient de moins en moins perceptible, et les effets sonores de modulation vont prédominer sur l’échantillon originel.
Pour le compositeur Cort Lippe (Lippe, 1993), la synthèse granulaire qui utilise des grains avec une forme d’onde synthétique pourrait être assimilée historiquement au mouvement de musique électronique (Elektronische Musik) de l’école de Cologne (Eimert et Stockhausen, 1956), tandis que la granulation temporelle ferait plutôt partie du monde de la musique concrète (Schaeffer, 1966), car ici, il s’agit d’un son enregistré qui est ultérieurement manipulé et transformé. Vu que les sons enregistrés appartiennent usuellement au monde sonore du réel, on pourrait jouer avec le seuil de reconnaissance d’une source originale en réalisant une déconstruction granulaire au moyen de la variation du point de lecture dans l’échantillon. Cet point de lecture est appelé onset time. On pourrait donc lire l’échantillon d’une façon linéaire continue (on écoute la source presque sans altération), et commencer à bondir ensuite de façon aléatoire et discontinue jusqu’à ne plus reconnaître la source d’origine. Bien évidemment, le continuum entre la reconnaissance et la non reconnaissance de la source sonore peut être exploité également par la modification d’autres paramètres comme la durée du grain, la densité, et la transposition des grains [57].
La transformation granulaire d’un objet sonore naturel peut affecter sa signification d’origine et créer des images métaphoriques. Pour bien exploiter l'utilisation de la métaphore sonore dans un discours musical, il faut se rabattre sur l'importance de deux concepts fondamentaux et caractéristiques de la temporalité du phénomène sonore, la transformation et le geste. La transformation est importante, car elle est le principal élément qui englobe la micro-transformation de l'objet sonore, et la macro-transformation globale dans une oeuvre (contexte, masse sonore, structure, etc). Donc, on va transformer des métaphores comme on transforme le son et la structure d'une pièce (Wishart, 1985). Par exemple, dans ma composition Móin Mór (1995), une voix transformée au moyen d’une granulation récite un poème anonyme de l’Irlande du huitième siècle. Cette transformation donne la sensation que la voix est faite de pierre; la voix nous fait donc penser aux monolithes de l’époque celte. Un autre exemple pourrait être une voix granulée, mais de façon stochastique. Ici on crée un geste musical au moyen de la granulation qui nous rappelle un essaim d’insectes, mais la source de la granulation est une voix humaine. On a comme résultat une image métaphorique de petits hommes qui volent comme des petites bêtes. Je traiterai davantage la transformation granulaire des sons réels et la création des images métaphoriques dans le dernier chapitre, en montrant des exemples concrets dans mes compositions et dans les compositions d’autres auteurs.
a.4) Synthèse croisée par granulation.
Cette technique est simplement la translation de l’idée de croisement dans le domaine du quantum sonore. On sait que la synthèse croisée c’est l’affectation de caractéristiques internes d’un son à un autre son. Par exemple, en utilisant la technique de la convolution on peut effectuer le croisement de deux signaux sonores, un qui fonctionne comme input et l’autre qui fonctionne comme excitation (impulse response). On multiplie les composantes spectrales des deux signaux. Les composantes qui sont égales ou qui se rapprochent vont être renforcées et les composantes qui divergent auront tendance à disparaître; on aura donc comme résultat un son intermédiaire entre les deux sons originaux [58]. Par exemple, si on prend l'analyse de l'enveloppe de l’aboiement d'un chien et on l'applique à l’analyse d’une trompette, on obtient le son d'une trompette articulée comme l’aboiement du chien. La convolution nous donne la possibilité de créer une grande diversité de sons hybrides et des images métaphoriques très riches.
Une autre technique digitale intéressante qui utilise l’idée de croisement est la transformation d'un objet sonore qui en devient un autre. On analyse par FFT deux sons différents, et ensuite on fait une re-synthèse en interpolant les composantes spectrales des deux sons. Ainsi, on peut passer par exemple d'une voix humaine qui chante une note au son d'un violon qui joue la même note, sans s’en en apercevoir. Cette technique a ses limitations, occasionnés par la difficulté de créer une transition naturelle entre deux sons qui sont assez différents.
Le croisement granulaire diffère des deux techniques de synthèse croisée décrites, car nous n’avons pas d’analyse préalable [59]. On parle ici d’un croisement par mixage, mais on mélange deux signaux sonores au niveau du quantum sonore. Le mixage peut se faire de façon linéaire, en respectant la durée originelle de chaque son; la périodicité des grains ici est synchrone, mais on pourrait aussi contrôler le rythme des grains de façon apériodique, ou aléatoire, et réaliser en même temps un étirement de deux sons. Cette deuxième technique constitue une innovation dans le cadre de la synthèse croisée, et elle a l’avantage de ne pas utiliser un temps de calcul long. Elle a également une possibilité de variation de l’enveloppe et de la durée de chaque grain, modalité qui donne une gamme intéressante d’effets de texture qu’on peut appliquer au croisement.
J’ai crée un algorithme de croisement granulaire pour le logiciel GiST qui a été développé à l'IRCAM (Eckel et Rocha Iturbide, 1995). Je traiterai plus en détail les effets sonores produits par cet algorithme dans le quatrième chapitre.
5.- Sons granulaires composés et superposition des nuages granulaires.
La composition électroacoustique commence au moment où l’on crée un nuage granulaire. Cet nuage pourrait être plus ou moins complexe et avoir différentes caractéristiques de timbre comme nous l’avons vu auparavant (nuage simple avec une seule forme d’onde, nuage où la forme d’onde évolue, nuage harmonique, nuage hybride, etc). Néanmoins, le processus de composition commence à s’enrichir quand on mélange plusieurs nuages granulaires. Chacun de ces nuages équivaudrait à une voix, et il faudrait programmer plusieurs instruments granulaires en parallèle pour pouvoir composer toutes les nuages dans un même processus. De cette manière, chaque nuage simple ou composé pourrait avoir un timbre, une distribution spatiale et une densité différents (Fig. 27). Un instrument suffisamment puissant pourrait même avoir la possibilité d’effectuer une distribution spatiale des grains dans 4 ou 8 canaux. Malheureusement, pour pouvoir mettre en marche tous ces instruments avec toutes ces possibilités en même temps, on aurait besoin d’un ordinateur très puissant, et l’exécution de la synthèse en temps réel serait presque impossible. Pour cette raison, les compositeurs sont pour l’instant obligés de composer sur le papier l’évolution de chaque nuage ou de chaque voix, de synthétiser séparément chaque nuage, et ensuite, de mixer tous les nuages dans le studio d’enregistrement selon un plan préconçu. Il serait toutefois génial d’avoir un seul super- synthétiseur en temps réel, capable d’effectuer toutes ces opérations en même temps. Laissons cette possibilité pour le futur, quand le perfectionnement des ordinateurs personnels le permettra.
J’ai parlerai plus en détail de la composition par superposition de nuages granulaires dans le dernier chapitre [60].
II.- Application de la synthèse granulaire sur différents systèmes informatiques.
J’essaierai de décrire plusieurs applications de la synthèse granulaire asynchrone et presque synchrone sur différents systèmes informatiques, afin d’établir une comparaison et avoir une idée plus nette du potentiel de ces techniques. Bien évidemment, il serait presque impossible de les nommer toutes. Je ferait donc référence aux applications les plus connues et à une application de moi-même réalisé avec les logiciels Csound et PatchWork. Toutefois, je donnerai à la fin de cet travail une liste étendue de toutes les applications que je connais, accompagnées d’une brève description ainsi que des références de ses auteurs.
1.- Programmes créés pour le contrôle de la synthèse granulaire.
a) Application de Roads 1981. MIT Music 11.
J’ai traité dans le premier chapitre les premières applications de la synthèse granulaire, dont celle de Gabor, et celle de Curtis Roads faite pour l’ordinateur Borroughs B6700, avec le programme Music V. En 1981, pendant qu’il était chercheur associé au studio de musique expérimentale à l’institut de technologie de Massachusetts (MIT), Roads a amélioré son application de 1975, qui avait certaines limitations en ce qui concernait le contrôle des paramètres du grain. La nouvelle application a été faite sur un système informatique PDP-11/50, avec l’utilisation du programme Music 11. Cette application a bénéficié d’un taux d’échantillonnage plus large (40 Khz), d’une largeur d’échantillon plus grande (16 bits), et d’une capacité de diffusion sonore quadraphonique (4 16-bit DACs). D’autre part, Roads a également développé une application de "granulation temporelle" [61] en utilisant des échantillons d’instruments de percussion et de saxophone pour réaliser plusieurs expériences. Il a crée des tendency masks [62] pour contrôler la densité du nuage, l’amplitude des grains, et l’ordre de la granulation des échantillons préparés d’avance, mais il n’a pas utilisé de tendency mask pour la durée des grains, mais seulement une fonction randomisée entre deux valeurs. Cette application de granulation temporelle a été la première conçue pour un ordinateur, et elle a bénéficié d’une qualité sonore de haut résolution.
b) Synthèse granulaire avec Csound et PatchWork.
Avec l’apparition et le développement des ordinateurs personnels au début des années 90, Roads a décidé de recréer les deux applications de synthèse granulaire de 1981 (Roads, 1981) sur un ordinateur Macintosh Quadra (Roads, 1992) en utilisant le logiciel Csound (Vercoe, 1986) pour réaliser la synthèse, et le logiciel C++ comme appui pour créer les scores de Csound. Il a appelé GRANULATEUR l’application de synthèse granulaire à partir des échantillons, et SYNTHULATEUR [63] celle de synthèse granulaire à partir des ondes synthétiques. J’ai connu ces applications en 1993 à l'IRCAM où j’ai été en contact avec Roads. J’ai commencé à travailler sur elles, car je souhaitais alors utiliser différentes techniques de synthèse granulaire pour créer la partie électronique d’une composition mixte que je réalisais à l’IRCAM. De plus, grâce à la découverte de quelques articles écrits par Truax, je m’étais déjà intéressé aux techniques granulaires et j’avais commencé ma thèse de doctorat sur ce sujet. En travaillant avec ces applications, j’ai réalisé qu’elles n’étaient guère pratiques à cause de la difficulté du langage de programmation C++, et d’autre part, parce que le contrôle stochastique de paramètres n’avait pas été complètement développé par Roads. J’ai donc décidé de conserver les orchestres conçues par lui, et d’utiliser un logiciel plus aimable pour générer les scores, c’est-à-dire PatchWork (Laurson, Rueda, Duthen, 1993), un environnement interactif pour la composition et le contrôle de la synthèse sonore développé à l'IRCAM. Ce logiciel nous permet de programmer et de faire tourner des programmes Lisp par l’intermédiaire de patches graphiques et de manipuler des objets algorithmiques que l’on peut brancher les uns sur les autres. On a développé aussi à l'IRCAM un interface entre PatchWork et Csound appelé PW.CSOUND/EDIT-SCO (Malt & Pottier, 1993) grâce auquel j’ai pu développer un patch pour produire les scores de Csound.
J’ai un peu traité le logiciel Csound dans le premier chapitre. Cet environnement de programmation musicale crée à l'institut de technologie de Massachusetts (Vercoe, 1986) a été basé sur les concepts musicaux d’orchestre et de score (partition). L’orchestra serait la partie du programme chargée de créer les instruments qui vont jouer, et le score la partie du programme qui joue chaque instrument. Au début du deuxième chapitre, j’ai décrit l’instrument de base nécessaire pour effectuer la synthèse granulaire (Roads, 1991) (Fig. 2). On peut facilement créer cet instrument en utilisant un patch d’orchestre de Csound. La complexité de la synthèse granulaire ne se trouve pas dans l’instrument lui-même, mais dans l’exécution de l’instrument. Le contrôle stochastique de tous les paramètres du grain (amplitude, fréquence, durée, forme d’onde) doit être appliqué avec l’aide du score de Csound, mais l’écriture de milliers d’ordres pour contrôler les grains est impossible sans l’appui d’un logiciel programmé pour écrire les ordres d’exécution de chaque grain, c’est-à-dire, d’un logiciel tel que PatchWork.
Dans la figure 35 on peut voir le patch d’orchestre construit par Roads pour la génération des grains synthétiques. Il y a dix formes d’ondes différentes: la première contient l’harmonique fondamental, la deuxième contient le premier et le deuxième harmoniques, la troisième contient le premier, le deuxième, et le troisième harmoniques, et ainsi de suite [64]. On utilise une enveloppe gaussienne pour tous les grains, ce qui fait que la richesse du timbre est due uniquement à la diversité de formes d’onde et non par les enveloppes du grain. Les autres paramètres de contrôle sont: amplitude, fréquence, durée de grain, temps de déclenchement, et localisation spatiale. La densité et de la largeur de bande sont des paramètres qui existent comme conséquence du contrôle du temps de déclenchement et de la fréquence des grains.
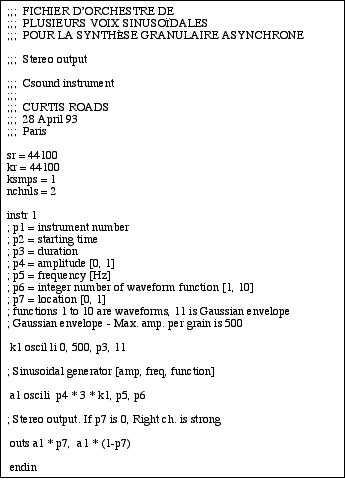
Figure 35.- Patch d’orchestre pour la génération des grains synthétiques.
Observons à présent le patch de l'orchestre du programme GRANULATEUR de Roads pour la granulation d’un ou de plusieurs échantillons (Fig. 36).
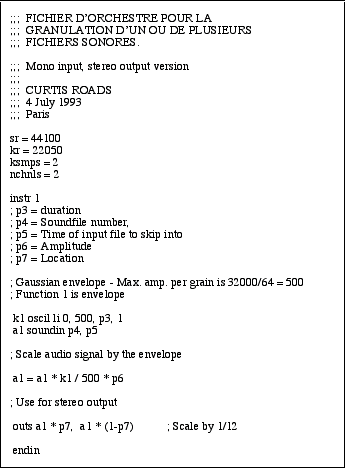
Figure 36.- Patch d’orchestre pour la granulation d’un ou de plusieurs échantillons.
Ce patch nous permet de contrôler la durée du grain, l’amplitude, le numéro de fichier sonore, la date de lecture du fichier sonore, et la localisation spatiale de chaque grain.
Comme je l’ai signalé auparavant, les patchs de l'orchestre ont été bien conçus par Roads, mais par contre, les patchs de contrôle avaient un langage de programmation compliqué. De plus, Roads n’a pas contrôlé tous les paramètres en utilisant des tendency masks. Il a donc fallu créer un patch avec l’aide de PatchWork pour développer un contrôle stochastique pour tous les paramètres et pour pouvoir créer ainsi des nuages granulaires dont la structure interne et externe changeraient de manière fine et continue dans le temps, grâce au contrôle de leur densité, de leurs limites inférieures et supérieures de fréquence, de la durée des grains, de la régularité ou l’irrégularité du rythme stochastique générée par les dates de déclenchement des grains, du changement de la couleur du timbre des grains, du changement de leur amplitude, etc.
Le logiciel PatchWork s’est avéré idéal pour le contrôle des tendency masks, car on utilise des tables graphiques avec lesquelles on peut générer leur valeur sans les écrire à la main (Figure 37). L’utilisation de ces tables est fondamentale dans ma contribution personnelle. Aussi, l’idée de rendre possibles une régularité et une irrégularité de l’algorithme qui contrôle le rythme des grains a été fondamentale pour enrichir le facteur temporel, car la génération aléatoire des grains entre deux valeurs différentes donne une texture rythmique trop homogène. De plus, j’ai décidé d’utiliser un algorithme d’une équation de chaos qui altère l’algorithme aléatoire, et qui donne une qualité différente au rythme stochastique.
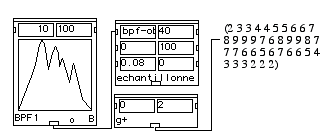
Figure 37.- Graphique BPF de PatchWork avec laquelle on peut dessiner une enveloppe qui donne une série de valeurs numériques.
Une autre avantage d’avoir utilisé PatchWork pour le contrôle du score de Csound c’est qu’on peut substituer dans mes patches la façon de déclencher les grains dans le temps. On peut remplacer facilement l’équation du chaos que j’utilise par des objets de la librairie d’objets stochastiques de PatchWork (alea.pw), tels qu’une chaîne de Markov, un mouvement brownien, une distribution de poisson, d’autres équations du chaos, etc. La flexible structure modulaire de PatchWork nous permet ce type des changements et enrichie les possibilités du contrôle.
Les paramètres de contrôle de mes patches sont les suivantes:
1.- Contrôle de densité du nuage granulaire.
C’est la génération d’une quantité plus ou moins élevée de grains par seconde. On peut stipuler une variation de densité grâce à une graphique BPF (Figure 37). Le changement de densité peut créer un processus où l’on passe d’un rythme stochastique des grains à une masse uniforme qui peut devenir du bruit blanc.
2.- Contrôle des limites minimale et maximale de la largeur de bande.
Il est possible de contrôler la largeur de bande de fréquence pour le patch de synthèse granulaire des grains synthétiques. On utilise un tendency mask avec deux enveloppes (au moyen de deux graphiques BPF), une pour les valeurs minimales et l’autre pour les valeurs maximales. Des valeurs aléatoires sont générées entre ces deux courbes de valeurs. Ce contrôle temporel peut produire des glissandi granulaires.
3.- Contrôle de la durée du grain.
On contrôle également le changement de la durée du grain en utilisant des valeurs aléatoires générées entre une enveloppe pour la borne minimale et une autre pour la borne maximale. Ce paramètre nous permet de créer des processus entre les grains assez longs qui sont perçues comme fréquence (des grains d’une durée minimale de 10 msecs avec au moins deux périodes) [65], et des grains assez courts qui sont perçus comme du bruit (des grains d’une durée inférieure à 10 msecs).
4.- Contrôle de la régularité et de l’irrégularité du rythme stochastique généré à partir du temps de déclenchement des grains.
On contrôle les temps de déclenchement des grains de manière stochastique en utilisant deux enveloppes (des valeurs de délai minimales et maximales de déclenchement), mais on peut déterminer si on souhaite avoir un rythme régulier homogène, ou un rythme irrégulière hétérogène, et travailler ainsi avec le rythme du nuage granulaire (Figure 38).
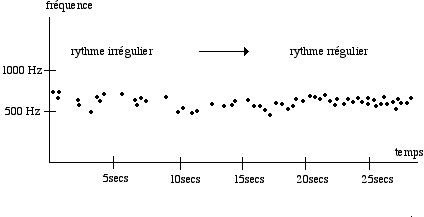
Figure 38.- Contrôle de la régularité et de l’irrégularité du rythme stochastique généré à partir du temps de déclenchement des grains.
5.- Contrôle du changement de timbre des grains.
Ce paramètre fonctionne de manière différente dans les deux programmes (SINTHULATEUR et GRANULATEUR). Pour la synthèse de grains synthétiques on peut contrôler le changement de type d’onde de chaque grain. Supposons que nous avons huit formes d’onde différentes et que nous voulons aller graduellement de la forme d’onde 1 (onde sinusoïdal pure) à la forme d’onde 8 (composée par les premiers huit harmoniques naturels). On peut dessiner deux graphiques BPF qui génèrent des valeurs aléatoires entre deux valeurs, minimale et maximale. On peut commencer par les valeurs 1 et 3, après 2 et 4, et ensuite 5 et 8. De cette manière on aura un changement stochastique graduel de timbre.
Pour le cas de la synthèse granulaire à partir de sons enregistrés, j’ai créé un patch où l’on peut effectuer une sélection des échantillons préparés à l’avance, et de cette manière, établir un passage graduel entre différents sons (voir figure 31) [66]. Par exemple, on pourrait effectuer un processus avec trois sons: basson, clarinette et hautbois, qui ont des timbres différents mais qui sont proches en tant qu’instruments; on pourrait aussi effectuer un passage entre différentes voix humaines de même registre, mais de timbre différent. Une fois de plus, pour créer ces processus on utilise un tendency mask avec deux enveloppes, une pour l’échantillon minimal et un autre pour l’échantillon maximal; c’est-à-dire, que chaque échantillon a un numéro, et ainsi on peut réaliser un processus semblable à celui des formes d’onde que l’ont vient de décrire dans le paragraphe précédent. Pour ma composition Transiciones de Fase réalisé à l'IRCAM, j’ai créé un processus qui comportait 12 échantillons originaires d’un même son de trompette. J’ai manipulé ce son au moyen d’un pitch-shifter, la durée du son a resté toujours la même, mais à chaque nouvelle manipulation, j’ai transposé les partiels du spectre. De cette façon, il y a eu une évolution du timbre vers les harmoniques aigus du son originaire de la trompette.
J’ai également crée un patch de granulation temporelle où l’on peut granuler un son dans le temps avec des dilatations ou contractions possibles. On peut déterminer la section spécifique du son à lire (offset), et la direction de lecture (en avant ou en arrière), ou lire de façon stochastique d’un point à un autre. Ainsi, on peut changer le timbre d’un son de différentes manières [67]. Le contrôle de lecture de l’échantillon se fait en utilisant un tendency mask avec deux enveloppes pour les valeurs minimale et maximale de l’offset.
La synthèse croisée par granulation est faisable avec deux échantillons ou plus, et on peut déterminer le pourcentage de lecture de chaque échantillon grâce aux deux graphiques BPF pour la lecture minimale et maximale du nombre de l’échantillon [68].
7.- Contrôle de l’amplitude du grain.
On peut contrôler l’amplitude de chaque grain de façon stochastique de même que les autres paramètres. Sur ces patches, je n’avait pas beaucoup travaillé avec le paramètre de l’amplitude en utilisant des tendency masks, mais plutôt avec une valeur minimale et une valeur maximale fixées pour donner simplement un peu de profondeur (volume tridimensionnel) au nuage granulaire; néanmoins, l’utilisation de deux enveloppes pour le contrôle de l’amplitude est possible au moyen de deux graphiques BPF.
8.- Contrôle de la localisation spatiale des grains.
On contrôle la localisation spatiale des grains en utilisant des valeurs aléatoires générés entre deux enveloppes. De cette manière on peut générer des grains dans certaines régions spatiales précises, et ces régions peuvent changer dans le temps [69].
c) Synth-O-matic.
Curtis Roads a crée un programme de synthèse granulaire au moyen de grains synthétiques avec le logiciel Synth-O-matic de James McCartney (copyright 1990) en 1991 et 1995. L’avantage de ce logiciel est qu’il fonctionne avec un ordinateur Macintosh 68k, et donc, qu’on a la possibilité de créer des nuages granulaires avec un ordinateur personnel. Avec la première version du programme, on pouvait obtenir une forme d’onde dessinée ou créée dans un menu (FM table fill, Cheby fill, Fourier Fill, Gbuzz table fill), mais seulement une forme d’onde pour toute la période de synthèse. On pouvait dessiner de la même manière une enveloppe pour le grain, ou choisir une enveloppe Hanning, Welch ou Parzen, mais on pouvait utiliser seulement une enveloppe pour tout le temps de synthèse. D’autre part, on pouvait choisir une fréquence centrale fixe avec une largeur de bande fixe autour de cette fréquence, une durée du grain fixe et une densité du nuage fixe. Comme on peut observer, dans cette première version il n’y avait pas de contrôle temporel des paramètres, et donc, l’utilisation de ce logiciel pour la composition a été fortement limitée. Néanmoins, ce logiciel s’est avéré idéal pour faire des essais, créer des textures qui peuvent servir ensuit pour réaliser des convolutions avec d’autres sons, etc. Aussi, ce logiciel a montré la puissance de la synthèse granulaire avec des grains synthétiques, grâce à l’infinité de formes d’ondes qu’on pouvait utiliser pour créer les nuages.
La deuxième version du programme de Roads (1995?) a finalement résolu le problème de l’absence de contrôle avec la création des enveloppes au moyen de graphiques où l’on pouvait dessiner la variation de la fréquence centrale, celle de la largeur de bande, celle de la valeur globale de la densité, celle de la durée du grain, et celle de l’amplitude du nuage granulaire. Seules l’enveloppe du grain et la forme d’onde sont restées fixes pendant toute la période de synthèse.
Avec un ordinateur Macintosh Quadra, on peut utiliser cette deuxième application et obtenir le calcul de la synthèse assez vite. Je crois qu’avec ce programme on peut bien explorer la synthèse granulaire asynchrone par ondes synthétiques et créer des nuages fort intéressants qui évoluent dans le temps. Néanmoins, l’impossibilité de varier la forme d’onde ne nous permet pas d’avoir une véritable évolution du timbre, et ce paramètre est fondamental dans la synthèse granulaire.
d) Cloud Generator Model 1.
Une autre application de synthèse granulaire développée par Roads en collaboration avec John Alexander (1995) pour l’ordinateur Macintosh c’est le logiciel Cloud Generator Model 1 qui nous permet d’effectuer la synthèse granulaire synchrone et asynchrone, en partant des ondes synthétiques, ou par granulation temporelle d’un échantillon.
Pour le cas de synthèse granulaire par ondes synthétiques, on peut choisir entre une onde sinus carrée ou triangulaire ou importer une onde enregistrée sur un fichier sonore. Pour la granulation temporelle on peut choisir un échantillon et déterminer le temps du début de lecture (offset). Cependant, on est limité à lire l’échantillon dans une seule direction.
Les paramètres de contrôle de ce logiciel utilisent l’idée d’événements déjà développée par Roads dans ses premiers logiciels. Les paramètres de contrôle sont les suivants:
- Densité initiale et densité finale.
- Amplitude initiale et amplitude finale.
- Limite supérieure et limite inférieure de la largeur de bande .
- Position initial et position final de la localisation spatiale stéréo, avec la possibilité de randomiser le parcours des grains.
- Durée initial et duré final du grain, ou option de durée aléatoire entre deux valeurs fixes.
- Dispersion aléatoire (Random Scatter) ou évolutive des grains .
Ce logiciel est déjà plus sophistiqué que celui développé avec le logiciel synth-O-matic, car on peut effectuer la synthèse granulaire en partant d’un échantillon, aussi, on peut avoir les deux modalités de synthèse granulaire synchrone et asynchrone. La largeur de bande est contrôlée ici d’une manière plus fine, grâce au contrôle individuel des limites inférieure et supérieure, mais l’évolution de ces deux paramètres et de tous les autres paramètres du logiciel est linéaire et ceci constitue une limitation du point de vue du contrôle fin par rapport à l’utilisation de graphiques dans la deuxième version de Synth-O-matic.
2.- Applications de synthèse granulaire en temps réel.
Les problèmes majeurs des méthodes de synthèse par ordinateur ont été toujours d’une part, la limitation de mémoire RAM des systèmes informatiques utilisés, et d’autre part la limitation de la vitesse du temps de calcul de ces systèmes. L’impossibilité d’avoir des résultats immédiats a ralenti les processus d’expérimentation qui ont parfois été trop longs, à cause de la lenteur de calcul des machines. Pendant quelque temps, seulement les grands ordinateurs ont été capables de réaliser le calcul de synthèse en temps réel, mais l’accès à ces ordinateurs a été limité par leur coût excessif. De nos jours, grâce au développement de la technologie, on pourra bientôt développer des systèmes de synthèse en temps réel pour des machines accessibles au grand public.
Les avantages du temps réel d’un système informatique sont principalement l’économie du temps pour la création de sons, qui nous donne plus d’espace pour la composition musicale, mais aussi, la possibilité de contrôle de la synthèse par un interprète. On peut construire un système de contrôle sophistiqué et ensuite apprendre à le maîtriser comme s’il s’agissait d’un instrument. Cette nouvelle possibilité permet la création d’un rapport direct entre la cause et l’effet, entre un geste musical humain spontané et une réponse immédiate de l’ordinateur. L’interaction en temps réel avec l’ordinateur permet aussi le changement constant des paramètres de contrôle de synthèse. L’interprète ou le compositeur peuvent par exemple modifier de manière instantanée les paramètres de granulation (changement de densité, de rythme, etc). De plus, on peut produire toujours le même son mais avec de légères modifications à chaque fois, et créer ainsi un élément de nouveauté qui ne change pas la structure globale des sons. D’autre part, l’interaction n’est pas limitée au compositeur et à l’instrumentiste, car on peut réaliser des systèmes d’interaction entre un programme de synthèse et le public, au moyen de différents senseurs qui peuvent détecter le mouvement de gens dans un espace déterminé. On parlera de l’aspect esthétique de cette dernière possibilité dans le dernier chapitre.
Je vais parler du premier système de synthèse granulaire en temps réel conçu par Barry Truax en 1986 (Truax, 1987), et aussi d’un système postérieur conçu pour la station ISPW de l'IRCAM (Lindemann, Starkier & Dechelle, 1990) par Cort Lippe (Lippe, 1993). Grâce au développement de la technologie, il y a eu ces dernières années une grand développement des systèmes de synthèse granulaire en temps réel, mais je ferai seulement une brève description de ceux-ci dans la section de l’APPENDICE.
a) Synthèse granulaire avec le processeur DMX-1000 DSP micro-programmable. GSX et GSAMX.
L’application de synthèse granulaire en temps réel de Barry Truax a été à l’origine d’une préoccupation pour créer des variables de contrôle capables de donner au musicien un rapport direct entre les data du niveau le plus bas (Lower level data) et les stratégies de composition et de gestes musicaux qui se trouvent à un niveau macro (Truax, 1988, 1993). Il a décidé d’utiliser le DSP micro-programmable DMX-1000, un de premiers processeurs de signaux digitaux (Wallraff, 1979). Pour contrôler le DMX-1000 , il a utilisé un PDP Micro 11 (LSI-11/23+).
Truax développe deux programmes pour réaliser la synthèse granulaire en temps réel, le GSX et le GSAMX, et trois différents modèles de synthèse. Le premier modèle (AS synthèse additive) est constitué par un oscillateur avec fréquence, une forme d’onde et une durée variables [70]; le deuxième modèle (FM modulation de fréquence) utilise un couple d’oscillateurs FM avec ratio (c:m), fréquence du carrier, durée, et index de modulation variables; le troisième modèle (SAM échantillonnage) utilise un échantillon de durée et d’offset variables pour la génération de grains.
On a parlé au début de ce chapitre des enveloppes de grains dans la synthèse granulaire, et on a décrit les enveloppes utilisées par Truax dans ce système. L’utilisation d’enveloppes qui peuvent changer en temps réel a permis l’évolution du timbre des grains, mais la linéarité des enveloppes et leur limitation à 3 segments ont créé des problèmes de sidebands. Néanmoins, ces effets pourraient être désirables pour l’utilisateur car ils peuvent parfois enrichir le timbre des grains. D’autre part, Truax a profité de la possibilité de variation de l’enveloppe en temps réel, et il a utilisé cette enveloppe pour contrôler l’amplitude du carrier et des fréquences modulantes pour le modèle FM. Aussi, la symétrie des enveloppes a permis la lecture de l’échantillon dans les deux directions.
Le système de Truax a une capacité de 20 voix différentes pour le modèle de synthèse additive (AS), de 8 pour le modèle FM, et de 20 pour le modèle de lecture d’échantillons (SAM). La moitié des voix est assignée automatiquement au canal droit, et l’autre moitié au canal gauche. Par rapport à la densité, il faut prendre en considération qu’elle dépend de la durée des grains. La durée minimale du grain dans ce système est de 8 msecs; avec cette durée minimale on peut avoir 125 grains par voix. Donc, les modèles AS et SAM peuvent avoir jusqu’à 2500 gps (grains par seconde), pendant que le modèle FM peut seulement avoir jusqu’à 1000 gps. 2500 gps et 1000 gps, sont des quantités de grains considérables, particulièrement quand il s’agit d’une synthèse granulaire en temps réel. Ce potentiel est fondamental dans l’innovation du système de Truax, car avec des densités pareilles on peut créer des effets de texture et de volume très particuliers.
Pour le modèle de lecture d’échantillons, Truax a crée deux versions, la première utilise un échantillon fixe assez court (seulement 4032 échantillons, c’est-à-dire, de 150 à 170 msecs) enregistré sur la mémoire du DMX. La petite taille de l’échantillon est produite par la mémoire de 4 Kword du DMX (Voir dans ce même chapitre: granulation temporelle en temps réel d’un son alimenté à l’entrée). La deuxième version réalise la granulation en temps réel à partir d’un son continu alimenté à l’entrée du DMX, avec la mémoire de 4 Kword qui agit comme fenêtre mobile pour effectuer de courts délais entre les grains. Les délais sont limités à moins de 170 msecs pour la première version (soit à 80 msecs environ dans chaque direction si le délai s’effectue à partir de la moitié de la fenêtre), et à 170 msecs maximum pour la deuxième version (figure 29) [71].
La petite mémoire du DMX constitue la principale limitation de ce système de synthèse granulaire, car on ne peut pas effectuer des délais supérieurs à 170 msecs, et donc, le seule type de lecture possible d’un échantillon est celui qu’étire ou raccourcit un son dans le temps de façon graduelle. On ne peut pas bondir d’un endroit de l’échantillonne à un autre en totale liberté.
Les paramètres de contrôle dans ce système de synthèse granulaire sont les suivants:
1.- Fréquence centrale et portée de la fréquence (pour le AS et le FM seulement).
2.- Numéro d’offset des échantillons à partir du début et de la portée de l’offset (pour le SAM seulement).
3.- Durée moyenne du grain et portée de la durée.
4.- Délai entre les grains.
Par rapport à la fréquence de grains, on peut avoir une bande de fréquence fixe, mais on peut aussi changer et avoir un écart harmonique des fréquences qui va dépendre de la fréquence centrale de chaque voix. D’autre part, avec le modèle SAM on peut altérer la vitesse de la sortie du son, facteur qui occasionne une transposition de la fréquence de l’échantillon. Avec ce modèle, on peut avoir aussi un taux d’échantillonnage différent pour chaque voix, ce qui produit une transposition différente pour chacune d’elles.
Les paramètres avec un contrôle stochastique sont: fréquence des grains, durée des grains ou temps de délai, offset des échantillons (pour le modèle SAM), et index de modulation FM (pour le modèle FM). La limitation de ces contrôles stochastiques est qu’on choisit à chaque fois une portée différente pour la génération de valeurs aléatoires (fig. 18 c), mais cette portée ne peut pas s’élargir ou se raccourcir graduellement dans le temps d’une façon non linéaire (fig. 18 d et e). Pour pouvoir faire ceci, il faudrait avoir un contrôle individuel pour la valeur minimale de la porté et un autre pour la valeur maximale de la portée, en lieu d’avoir une valeur centrale, et une portée fixe spécifiée à partir de cette valeur centrale. Résoudre ce problème serait une chose simple et facile, mais il faut tenir compte que chaque compositeur a ses préférences personnelles par rapport au contrôle stochastique des paramètres.
D’autres possibilités de contrôle dans ce système sont la faculté d’arrêter et de faire recommencer les différentes voix, ce qui produit des changements de densité. D’autre part, pour le modèle SAM on peut affecter la vitesse de lecture d’un certain nombre de voix pour aller de deux à quatre fois plus vite, ou à la moitié ou à la quatrième partie de la vitesse; l’on crée ainsi des transpositions d’octave.
Avec le système de synthèse granulaire de Truax, on se trouve devant un outil de composition électroacoustique très puissant qui possède un grand nombre de variables. En utilisant ce système, on devient une sorte d’instrumentiste qui doit apprendre à maîtriser tous les paramètres pour les affecter en temps réel, en utilisant les différentes touches du clavier de l’ordinateur. En plus, Truax a crée des automatisations pour les valeurs des paramètres (ramps) qui font que les valeurs changent de façon continue (avec une augmentation ou une diminution), ou de façon aléatoire (Fig. 39). La vitesse de ces ramps est variable, et il est possible d’effectuer des accélérations et des ralentissements de vitesse. Aussi, les ramps peuvent être cycliques. Quand la valeur d’un ramp qui descend arrive à zéro, le ramp peut recommencer dans le sens opposée (dans ce cas de manière ascendante). Finalement, on peut à tout moment changer la valeur des ramps automatisés, ce qui rend le contrôle d’automatisation extrêmement flexible et interactif. Le seul désavantage des ramps est que leur vitesse est synchronisée et qu’ils sont interdépendants. Aussi, les processus qui sont déclenchés par les ramps ne sont pas trop perceptibles pour l’utilisateur. Truax a alors créé un deuxième programme d’automatisation qui utilise des tendency masks graphiques (GRMSKX). Ces tendency masks sont complètement indépendantes les uns des autres et ils ont l’avantage de décrire graphiquement l’évolution des valeurs de chaque paramètre.
En outre, Truax a crée un programme de contrôle pour affecter les fréquences de grains en utilisant des équations chaotiques non linéaires. Le programme GSKX utilise l’équation logistique (ou quadratic map): x(n+1) = r. x(n) . [1 - x(n)], et l’équation Gingerbread Man. Cette dernière équation est très dynamique car elle produit des répétitions périodiques suivies par des excursions chaotiques. Les équations chaotiques sont très intéressantes car elles reproduisent des processus structurels complexes semblables à certains processus qu’on peut observer dans la nature.
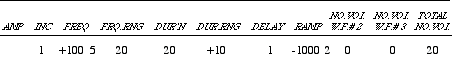
Figure 39.- Ligne de contrôle de variables synchrones. INC est l’incrément de la valeur du ramp, FREQ est la fréquence centrale moyenne, FRQ.RNG est la portée de la fréquence (largeur de bande), DUR’N est la durée moyenne du grain , DUR.RNG est la portée de la durée du grain, DELAY est le délai entre les grains, RAMP représente la direction du ramp et le temps en msecs entre chaque pas (augmentation), NO.VOI,W.F.# 2 est le nombre de voix de la forme d’onde 3. TOLAL NO.VOI. est le nombre total de voix. Pour le modèle FM , les variables de la forme d’onde sont substituées par l’index de modulation moyenne et par la portée de l’index de modulation.
Je parlerai en détail de ces équations et des différentes possibilités d’application sur les techniques de synthèse granulaire dans le sixième chapitre sur les algorithmes de contrôle utilisés par la synthèse granulaire [72].
Pour achever la description de ce système, je voudrais signaler certaines possibilités du contrôle qui n’ont pas été contemplées par Truax. Pour commencer, il n’a pas créé un contrôle afin d’avoir des nuages de texture hybride pour le modèle SAM, ce qui pourrait se faire avec une lecture de plusieurs échantillons de façon simultanée. Peut-être la raison de l’absence de ce contrôle se doit à des limitations de mémoire du DMX-1000. En tout cas, le mélange de différents timbres constitue un élément particulièrement intéressant dans la synthèse granulaire à partir des échantillons, et il est dommage qu’il n’ait pas pu appliquer cette technique à son système. Par rapport au modèle AS, il existe ici la possibilité de réaliser des nuages granulaires de texture hybride, mais on a seulement la faculté d’avoir trois formes d’onde différentes. Ceci constitue une limitation par rapport au différents programmes de Roads. Cependant, le modèle FM de Truax est très développé par rapport au changement de timbre de chaque grain, grâce à la variation du paramètre de l’index de modulation. La technique FM est sans doute plus facile à appliquer dans un système de synthèse granulaire en temps réel sans avoir à payer un coût trop élevé pour le temps de calcul de la machine.
Dans les années quatre-vingt-dix, Truax a poursuivi le développement de la synthèse granulaire en temps réel, et il a réalisé deux nouvelles applications qui travaillent avec le même type de contrôle du programme GSAMX . La première application a été faite pour un ordinateur ATARI et la deuxième pour un ordinateur MACINTOSH avec le programme MAX Opcode (Puckette, Zicarelli, 1990). Ces deux applications se servent d’une boîte DSP construite par Truax et son équipe, nommée QUINTESSENCE BOX. Une deuxième version de cette boîte vient d’être construite et on peut réaliser avec elle la synthèse granulaire sur 4 chenaux différents, ceci donnant la possibilité de réaliser une spatialisation des grains sur 4 différentes points dans l’espace.
b) Synthèse granulaire avec la station ISPW de l’IRCAM.
Le système informatique plus complexe pour effectuer la synthèse et le traitement de signal en temps réel est peut-être la station ISPW de l'IRCAM (Lindemann, Starkier & Dechelle, 1990), qui fonctionne sur un ordinateur NEXT. Le programme utilisé pour contrôler le processeur de signal est MAX (Puckette, 1991).
Malgré le potentiel de la station ISPW qui permet la création d’une application pour la synthèse granulaire à partir d’ondes synthétiques, ou bien la granulation temporelle à partir des échantillons, personne ne s’y intéresse jusqu’en 1993. Le compositeur Cort Lippe réalise la première application de granulation temporelle (granular sampling) [73] pour la ISPW (Lippe, 1993). Cette application est contrôlée par des processus non linéaires, et elle a été planifiée spécialement pour effectuer le contrôle granulaire par la détection des paramètres musicaux des instruments qui jouent en temps réel (Lippe & Puckette, 1992).
Les paramètres de l’application de Lippe sur la ISPW sont les suivants:
- Date de lecture de l’échantillon (Onset Time).
- Fréquence.
- Description de l’enveloppe.
- Amplitude maximale.
- Durée du grain.
- Taux de production des grains.
- Chevauchement des grains.
- Localisation spatiale des grains.
Pour le contrôle des paramètres, on peut utiliser des sliders , des boîtes numériques, ou bien les paramètres peuvent changer dans le temps de manière indépendante par l’automatisation des processus de contrôle. L’avantage de l’application de Lippe sur celle de Truax, est qu’on peut générer des nuages granulaires hybrides multi-timbrales (Roads, 1991), car on peut lire plusieurs échantillons en même temps, et avoir différents processus de granulation simultanés.
Lippe se sert des Tendency masks pour contrôler tous ses paramètres en utilisant des processus stochastiques tels qu’une marche aléatoire, des processus chaotiques, entre d’autres. De plus, il emploie des cartes algorithmiques pour pouvoir contrôler l’interaction entre les instrumentistes et l’ordinateur. La station ISPW utilise des outils d’analyse de signal audio en temps réel, et l’information de la fréquence et de l’amplitude des instruments peut être interprétée par l’ordinateur et utilisée pour le contrôle des différents paramètres de la granulation [74]. D’autre part, Lippe développe des paramètres de contrôle additionnels avec l’analyse spectrale des instruments qui jouent, permettant ainsi le contrôle du timbre des échantillons au moyen des changements de couleur de ces instruments.
La principale différence entre l’interface de contrôle du système de synthèse granulaire crée par Truax et celui de Lippe, est que le premier a été conçu pour être employé par un compositeur qui agit comme interprète. Ce système sert à la composition des nuages granulaires qui vont ultérieurement être mixés. Le système de Truax est trop lourd et difficile à transporter, et il a toujours accompli sa tâche dans le laboratoire électroacoustique. Aussi, l’interface de Truax permet l’improvisation, car on peut à tout moment jouer et décider le moment d’enregistrer le résultat, et ce résultat peut être ultérieurement édité.
La station ISPW de l'IRCAM a une puissance supérieure au système de Truax (si on compte avec trois cartes DSP), et ce système se transporte plus facilement. La ISPW et son logiciel MAX IRCAM ont été planifiés expressément pour l’interaction entre instrumentistes et ordinateur; donc, Lippe a simplement suivi le fonctionnement typique du système pour réaliser le contrôle de la granulation temporelle. Avec ce système, c’est en générale l’instrumentiste (et non le compositeur) qui contrôle les paramètres de la synthèse, et pour cette raison, on a généralement dans ce cas besoin d’un input plus important de la part du compositeur, car la synthèse générée en temps réel est le résultat sonore final. Alors, tout l’engrenage d’interaction doit être complexe et tous les processus de contrôle doivent être très précis et définitifs avant l’exécution de la pièce. On peut certainement avoir des situations où l’on veut obtenir des processus déclenchés par l’instrumentiste qui vont générer à chaque fois des sons granulaires différents, mais néanmoins, les mécanismes d’interprétation de l’ordinateur seront en général fixes.
Pour la planification d’un système de contrôle, le rôle de l’interaction sera toujours décidé à l’avance. Dans le système de synthèse granulaire de Truax, la responsabilité du contrôle appartient à l’utilisateur (en général un compositeur), et celui ci doit maîtriser le système pour arriver à créer de sons intéressants. L’utilisateur doit donc être spécialisé (Lovell R. et Mitchell D., 1995). Dans le système de Lippe, les processus de synthèse sont déjà préalablement structurés, et l’instrumentiste a seulement la responsabilité d’exécuter ses notes sans tenir compte du système. Ici l’instrumentiste réalise une interaction passive non dirigée (Lovell R. et Mitchell D., 1995). Le système d’interaction de Truax est ouvert, et souligne le processus de la génération de la synthèse, pendant que le système d’interaction de Lippe est prédéterminé et se concentre plutôt sur le produit final (Dannenberg, R. et Bates J, 1995).
Je traiterai davantage le côté esthétique de l’interaction des systèmes de la synthèse granulaire dans le dernier chapitre, et particulièrement l’interaction dans des installations sonores où le public devient un agent non spécialisé et qui n’est pas obligé de connaître le système [75].
NOTES DE PIE DE PAGE
[1] "Une des premières caractéristiques du son créé par la synthèse granulaire est sa qualité dynamique. Il est pratiquement impossible d'obtenir un son statique et sans variation. C'est l'exception, non la règle. Cette qualité est une réminiscence de l'environnement naturel où tous les éléments changent sans arrêt". (Truax, 1992c).
[2] Le système PODX, constitué par un processeur digital de signal DMX-1000 contrôlé par un PDP Micro 11.
[3] G. De Poli, A. Piccialli, and C.Roads, eds. 1991. "Representations of musical signals". Cambridge, Massachusetts: The MIT Press.
[4] En français, QSGS est: synthèse granulaire presque synchrone, et AGS est: synthèse granulaire asynchrone.
[5] Granulation de sons échantillonnés en français. On l’appelle aussi granulation temporelle.
[6] Terme inventé par Cort Lippe qui veut dire échantillonnage granulaire.
[7] Les FOF sont des grains avec une fonction d’onde formantique utilisées dans la technique de synthèse CHANT développé a l’IRCAM par Xavier Rodet. Les FOF ont servit au début pour simuler un synthétiseur à formants en parallèle, mais plus tarde on a essayé de les intégrer aux techniques d’analyse-synthèse (d’Alessandro,Rodet,1989), raison pour laquelle ils pourraient aussi former partie des techniques d’analyse-synthèse.
[8] Le méthode de chevauchement de flots de fréquence synchrone peut être aussi considéré dans le groupe des techniques de synthèse granulaire par formants qui sera analysé dans le troisième chapitre, puisque la synchronisation des fréquences peut produire des effets d’amplitude modulée caractéristiques des sons formantiques.
[9] Quasi-Synchronous Granular Synthesis.
[10] Robert Moog (1988) a fait varier le taux de répétition d’un grain (ou sa durée) entre 15 et 25 msecs. En lieu d’avoir des sidebands discrets il a obtenu une bande de bruit étroit continue centrée autour de la fréquence centrale. Il a décrit ce qualité du son comme "shimmering or animated" (miroitant ou animée), "la qualité caractéristique de la musique quand on utilise la synthèse granulaire" (Moog, 1988).
[11] Des techniques telles que CHANT (Rodet, Potard, Barrière, 1980) avaient été conçues pour utiliser toujours des flots réguliers, mais il y a quelques années Michael Clark avait suggéré que CHANT était une technique de synthèse granulaire, et qu’on pourrait donc contrôler les grains (ou FOF) d’une façon irrégulière (Clarke, 1988).
[12] Il faut dire qu’en ce moment-là, Roads n’avait pas invente le terme de "Quasi Synchronous Granular Synthesis".
[13] Certains flots étaient plutôt régulières et d’autres plutôt irréguliers.
[14] Voir le développement du logiciel GiST au quatrième chapitre.
[15] Voir la section sur les effets de la bande de fréquence.
[16] Les recherches de McAdams et Bergman (1979) et de MacKey (MacKey, 1984) avaient également été fondées sur l’élément psychoacoustique.
[17] Des chercheurs comme David Wessel (1973, 1979, 1982), J.C. Risset (1982), et Grey (1975, 1977) ont réalisé un étude approfondie du domaine du timbre; ils ont essayé de créer un "espace de timbres représentant de manière adéquate les différences perceptives....une sorte de carte d’aide a la navigation pour le compositeur intéressé par la structuration des aspects du timbre" (Wessel, 1973) . Cet espace de timbre est subjectif, non linéaire et discontinu, mais on a prouvé qu’il est possible de créer des transitions réguliers finement gradées entre différentes sons au moyen des interpolations de leurs spectres (J.C. Risset et D. Wessel, 1982).
[18] 80 millièmes de secondes par exemple. Comme il a été dit dans le premier chapitre, un grain qui dépasse les 50 msecs peut être considéré comme une petite note.
[19] Dans: G. De Poli, A. Piccialli, and C.Roads, eds. 1991. "Representations of musical signals". Cambridge, Massachusetts: The MIT Press.
[20] Tendency mask signifie la délimitation des paramètres stochastiques par certaines bornes, comme deux enveloppes entre lesquelles il y a un éparpillement de grains aléatoire.
[21] Les premières implémentations élaborées et appliquées après celui de Xenakis.
[22] Voir prochaine section.
[23] "Si on raccourcit la durée du grain dans le domaine du temps, le domaine de la fréquence augmente en compensation, et la largeur de bande est augmentée. Ce phénomène est connu comme "loi d’incertitude", comme référence au principe d’incertitude de Heisenberg par rapport à la position et la vitesse de l’électron, et il est en général décrit comme la relation inverse entre la fréquence et le temps" (Truax, 1994). Voir aussi la théorie de l’incertitude de Heisenberg dans le premier chapitre.
[24] Ircam Sound Processing Work Station (ISPW) qu’utilise un ordinateur NEXT et une carte DSP désigné a l’IRCAM.
[25] Je développerait plus loin les aspects techniques de la durée minimal du grain.
[26] Voir le cinquième chapitre, section sur le système GiST.
[27] Dans le projet GiST, j’ai beaucoup travaillé avec des macro-grains (de 100 à 300 msecs) mais avec des petits délais plus au moins réguliers (entre 10 et 30 msecs). Voir le cinquième chapitre pour plus de détails sur ce procédé.
[28] Cette idée d’imaginer une synthèse additive mais en utilisant des grains au lieu d’oscillateurs m’est venue récemment. Particulièrement parce que le défaut typique de la synthèse AGS c’est de ne pas envisager l’idée d’harmonie spectrale. On pense toujours en fonction d’une bande de fréquence qui génère des nuages granulaires plutôt bruiteux. Je développerai davantage cette idée dans d’autres chapitres.
[29] Quand la densité est grande, les bornes de fréquence supérieures et inférieures de la bande déterminent la forme du nuage par rapport à une écoute morphologique où l’on ne distingue pas la fréquence des composantes à l’intérieur du nuage.
[30] Voir le premier chapitre où Xenakis fait une critique à la musique traditionnelle qui utilise des sons fixes et invariables dans le temps: "Il est fort probable que l’échec des musiques électroniques dans la constitution de timbres nouveaux, mise à part l'insuffisance de la méthode sérielle, est dû en grande partie à la fixité des grains qui engendrent des structures en forme de paquets de spaghetti"(Xenakis 1971, pg 70).
[31] Comme on l’a déjà décrit dans la section sur la synthèse QSGS.
[32] Dans le sens musical, car Gabor avait déjà créé une sorte de granulateur de sons échantillonnés, mais il ne s’en est pas servi pour faire des expériences musicales.
[33] Un taux de succession de grains serait la même chose que le paramètre de densité.
[34] Turgid colored noises. (en anglais).
[35] Sur tout dans la synthèse granulaire QSGS et la AGS. En fait, le concept de texture sonore est inhérente dans ces deux types de synthèse.
[36] Voir figure 18 e.
[37] Dans son livre "On sonic art" , Trevor Wishart fait référence à des sons instrumentaux avec une granulation interne ou la non périodicité du grain contribue à une perception différente. "A-periodic grain has a bearing on the particular sonority of sizzle-cymbals, snare-drums, drum-rolls, the lion’s roar and even the quality of string sound through the influence of different weights and widths of bows and different types of hair and rosin on the nature of bowed excitation" (Wishart, 1985. pg. 40). Erickson, dans "Sound structures in music" fait référence à cette caractéristique et l’appelle rustle time.
[38] J’ai déjà parlé de la plupart des phénomènes de dépendance de ces deux paramètres dans la section précédente.
[39] Voir la section antérieur sur les effets de bande de fréquence.
[40] Truax poursuit de la façon suivante: "Ce concept a été courant dans les premiers travaux de psychoacoustique (Seashore, 1938), et jusqu’à 1967 (Olson, 1967). A ce moment, il a été remplacé par le paradigme stimulus-response de l’addition des composantes des ondes sinus pour matériel composé des fréquences, et composantes de bruit des bandes étroites avec sons apériodiques, particulièrement des avions (Kryter 1959)".
[41] "Dans certains cas, le résultat acoustique de la synthèse granulaire est semblable aux sons de l’environnement par rapport à leur complexité interne et leur texture statistique" (Truax, 1988). Voir aussi note 1.
[42] A ce moment là, la musique électroacoustique n’était pas très développée. C’est étonnant que Varèse ait pu imaginer des phénomènes sonores complexes sans pouvoir les réaliser.
[43] "La modélisation spectro-morphologique et sa faculté de contrôler le dessin spectral et dynamique, crée des mouvements réels et imaginés sans avoir besoin d’un vrai mouvement dans l’espace" (Smalley, 1986).
[44] Voir l’article de Smalley "Spectro-morphology and structuring processes" dans, "The language of electroacoustic music". Simon Emmerson éditeur, 1986.
[45] Ces trois types de mouvements internes de composantes sont décrits par Smalley dans son article (ibidem). La traduction directe de ces trois types de mouvement est la suivante: Flocked motion est un mouvement d’un troupeau ou d’une foule, stream motion est le mouvement d’un ruisseau, et contorted motion est un mouvement contorsionné ou convulsionné.
[46] Il y a déjà actuellement diverses applications qui tiennent en compte ce potentiel et qui utilisent au moins 4 canaux.
[47] Xenakis parle des nuances colorées du bruit blanc quand on varie les paramètres des nuages granulaires très denses.
[48] Avant Truax, Otis, Grossmann et Cuomo (1968) avaient développé une implémentation digitale de granulation temporelle de fichiers sonores.
[49] On a parlé de cet effet dans la section précédente sur les effets de densité.
[50] Truax appelle cet phénomène inner voices (voix internes). Il a utilisé cet effet dans ses compositions Pacific et Dominion, où "les voix ressemblent à un choeur distant de voyelles chantées" (Truax 1992b).
[51] Voir pied de page 40.
[52] En juillet de 1994 j’ai été invité par l’université de SFU à Vancouver, Canada, pour travailler avec le système de synthèse granulaire en temps réel de Barry Truax et composer une pièce pour bande digitale seule.
[53] Ce nuage est semblable au nuage harmonique de Truax qui utilise une transposition par changement de taux d’échantillonnage (Fig. 30), sauf qu’ici on n’a pas besoin d’effectuer une transposition car on a un échantillon différent pour chaque hauteur. L’avantage est que la qualité d’un son est meilleure quand on ne le transpose pas, mais le désavantage est qu’il faut faire jouer par un instrumentiste les différentes hauteurs désirées, ou les transposer auparavant et préparer les échantillons, et toutes ces opérations prennent du temps. Cependant, la qualité finale sera meilleure.
[54] Roads avait utilisé le terme monochrome pour définir un nuage AGS où l’on utilise des grains avec la même onde sonore; ici j’utilise le terme pour définir un nuage où l’on utilise le même échantillon, ou une série d’échantillons de la même source sonore (plusieurs notes jouées par un violon par exemple). Un nuage de texture monochrome est harmonique quand il s’agit de plusieurs échantillons avec des hauteurs claires et perceptibles, ou purement de texture quand on utilise un échantillon avec un spectre complexe, ou encore un échantillon d’un instrument, mais transposé de façon stochastique.
[55] Voir section sur la synthèse QSGS.
[56] Voir bande de fréquence cumulus dans la section sur les effets des bandes de fréquence.
[57] Avec une durée de grain très courte on perd la reconnaissance de la source sonore. Le même phénomène pourrait arriver avec une grande densité, ou avec une transposition stochastique.
[58] Si on prend l'analyse de la voix de quelqu’un (input), et qu'on la fait écouter en introduisant le conduit vocal d'une autre personne (excitation), on aurait comme résultat une hybridation entre les deux voix (Risset, 1991). Tracy Petersen a réalisé ce type de synthèse dans sa composition "Voices". Voir référence dans, RISSET Jean-Claude, 1991. "Timbre et synthèse des sons", dans "Le Timbre, métaphore pour la composition". Présenté par Jean Baptiste Barrière. Christian Bourgois Éditeur. IRCAM. Paris.
[59] Sauf dans le cas de la synthèse granulaire par ondelettes, que sera décrite dans une autre chapitre.
[60] Dans ma composition Transiciones de Fase, j’ai réalisé une section entière de la pièce avec une superposition de nuages granulaires (voir dernier chapitre).
[61] Qui n’existait pas dans l’ancienne application.
[62] Appelés par lui "slopes", pentes en français.
[63] En réalité, Roads n’a pas donné de titre à l’application de synthèse granulaire par grains synthétiques, mais puisque il a appelé l’application de granulation d’un échantillon: GRANULATEUR, je me suis permis de nommer l’autre application: SYNTHULATEUR.
[64] L’amplitude de toutes les harmoniques est toujours la même.
[65] Il faut au moins deux périodes pour être à mesure de percevoir la fréquence d’un son. Si notre grain est de 10 msecs il faudrait avoir une fréquence de 200 Hz, car une période de cette fréquence est équivalente à cinq msecs.
[66] On a vu dans ce chapitre comment Roads a établi trois modalités différentes de Granulation temporelle des sons échantillonnés. La troisième modalité constitue la "Granulation d’un ou de plusieurs fichiers sonores gardés dans la mémoire et l’exécution de leur grains de façon asynchrone". Bien évidemment, on pourrait simplement mélanger tous les sons en même temps et n’effectuer aucun processus, mais pour ceci on n’aurait pas besoin d’un tendency mask; il faudrait simplement établir une opération aléatoire entre le premier et le dernier son.
[67] Voir les sections sur la Granulation temporelle en temps réel d’un son alimenté à l’entrée et sur la Granulation temporelle asynchrone des sons échantillonnés dans ce chapitre.
[68] Voir synthèse croisée par granulation dans ce chapitre.
[69] Voir dans ce chapitre: effets paramétriques dans la synthèse granulaire asynchrone, distribution des grains dans l’espace.
[70] On peut choisir seulement entre trois formes d’onde différentes.
[71] Les délais pour la deuxième version s’effectuent toujours en arrière en partant de la date de lecture de l’échantillon qui s’effectue en temps réel.
[72] J’ai créé une application de l’équation chaotique logistique pour le logiciel de synthèse granulaire formantique GiST, développé à l’IRCAM (Eckel, Rocha Iturbide, 1995). Voir chapitre IV.
[73] Terme inventé par Cort Lippe pour nommer la technique de synthèse granulaire à partir d’échantillons.
[74] "Dans ma composition Music for Clarinet and ISPW, les data continues de la fréquence de la clarinette est utilisé pour contrôler la fréquence de grains, et les data continues de l’amplitude servent à contrôler les fenêtres des tendency masks de certains paramètres" (Lippe, 1993 pg 193).
[75] Dans le cas d’une installation sonore qui utilise des senseurs et où le public agit comme un agent non spécialisé et sans connaître le système, on a une interaction indéterminée, et la création des sons devient plus aléatoire. Dans un système de ce type, on doit structurer le système de contrôle en utilisant l’esthétique d’une oeuvre ouverte, dans laquelle, malgré les constantes transformations créées par le hasard, l’oeuvre reste homogène.