FOOTNOTES ON THIS CHAPTER ARE NOT YET IMPLEMENTED!
CHAPITRE III: REPRÉSENTATION GRANULAIRE DANS LES TECHNIQUES
D’ANALYSE / SYNTHÈSE.
"L’analyse mathématique peut encore saisir les lois des phénomènes. Elle nous les rend présents et mesurables, et semble être une faculté de la raison humaine destinée à suppléer à la brièveté de la vie et à l’imperfection des sens; et ce qui est plus remarquable encore, elle suit la même marche dans l’étude de tous les phénomènes; elle les interprète par le même langage, comme pour attester l’unicité et la simplicité de "l’univers" (Fourier, 1822).
Depuis le dix-huitième siècle, les mathématiciens on étudié la représentation en fréquence des signaux. Joseph Fourier (1822) est le premier à avoir stipulé que n’importe quelle fonction périodique peut être exprimée comme une somme de sinusoïdes (sinus et cosinus) de différentes fréquences, ce qu’on appelle aujourd’hui une série de Fourier. De cette manière, n’importe quelle courbe périodique, même discontinue, peut être décomposée en une somme de courbes parfaitement lisses. Les séries de Fourier ont été restreints à l’analyse de signaux périodiques, or, on sait bien qu’une grande partie des signaux sonores extraits des sons qui nous entourent ne sont pas périodiques, ou bien qu’ils sont plus ou moins périodiques, et que leurs composantes spectrales changent constamment dans le temps. Gabor (1947) a défini la représentation d’un signal dans un plan Temps-Fréquence (voir premier chapitre), c’est-à-dire, une représentation bi-dimensionnelle où chaque point correspond à un intervalle de temps limité et à un intervalle limité de fréquence. On peut facilement obtenir cette représentation avec la convolution d’un signal sur un point dans le temps avec un "grain", qui consiste en un signal de fréquence avec une enveloppe limitée temporellement (une fenêtre) qu’on applique à ce "grain" (Arfib, 1991). Ce procédé est équivalent à la transformée de Fourier à court terme (Short-Time Fourier Transform, ou STFT), approche qui a été développé ultérieurement à la théorie de Gabor. De nos jours, l’analyse d’un signal se fait dans la plupart des cas avec une fenêtre d’analyse équivalente à un "grain" qui existe dans le plan Temps-Fréquence. Ce "grain" où quantum sonore constitue la particule élémentaire de la représentation granulaire d’un signal. On a discuté dans le premier chapitre la vision continuiste de la matière relative aux séries de Fourier (Wiener, 1964). La théorie de Fourier a bénéficié l’analyse des signaux périodiques, c’est-à-dire, les caractéristiques de fréquence d’un son, mais elle n’a pas considéré l’aspect temporel (c’est-à-dire, le changement d’un signal dans le temps). Néanmoins, après les théories quantiques du son de Gabor, de Wiener et de Moles, différents mathématiciens ont pris conscience qu’il était important de trouver des algorithmes afin de bien représenter les deux domaines du son, celui de la fréquence et celui du temps. Cette tâche a été fort difficile, car il y a toujours des paradoxes quantiques qui se suscitent quand on veut trouver une représentation fine dans les deux domaines en même temps.
Le paradoxe d’indéterminisme de Heisenberg est applicable aux techniques d’analyse-synthèse. Quand on veut réaliser une analyse fine dans le domaine de la fréquence d’un signal, il faut utiliser une fenêtre (ou "grain") d’analyse longue, et par contre, quand on a besoin d’obtenir une bonne résolution dans le domaine temporel du signal, il faut utiliser une fenêtre d’analyse petite. Or, il y a des signaux sonores où l’on a besoin d’avoir en même temps une bonne résolution d’analyse dans les deux domaines. C’est le cas de la parole, où interviennent deux composantes très différentes: les voyelles (signal long et assez bien localisé en fréquence) et les consonnes (signal qui délivre une information sur des échelles de temps qui peuvent être très petites) (Meyer, Jaffard, Rioul, 1987). Les recherches de Gabor (1947) sur la représentation d’un signal dans le plan Temps-Fréquence avec l’utilisation des "grains élémentaires" d’analyse, ont favorisé des recherches ultérieurs qui ont abouti à la création de l’algorithme de la transformée de Fourier à fenêtre glissante (nommé aussi transformée de Fourier à court terme), c’est-à-dire, la réalisation de plusieurs analyses de Fourier dans le temps au moyen d’une fenêtre d’analyse qui se déplace. Or, l’inconvénient majeur de ce procédé est que la longueur de la plage de la fenêtre est fixée une fois pour toutes et que l’on ne peut pas analyser simultanément des phénomènes dont les échelles de temps sont différentes.
En faisant l’analyse spectrale de la parole au moyen des méthodes d’analyse-synthèse telles que le Vocodeur de Phase, on éprouve une inexactitude due au problème d’avoir une fenêtre d’analyse de taille fixe qui ne change pas dans le temps. Pour essayer de résoudre ce problème, on cherche un compromis entre le domaine du temps et le domaine de la fréquence en choisissant une fenêtre de taille moyenne, mais notre analyse reste pourtant inexacte. La technique d’analyse-synthèse qui utilise l’algorithme de la transformée en ondelettes (développé dans les années 80’s) a pu privilégier en même temps les différentes échelles de résolution d’un signal sonore. Les ondelettes sont des fonctions élémentaires (ou "grains" élémentaires) construites à partir d’une ondelette "mère" analysante. Ces fonctions se construisent par translation et contraction ou dilatation dans le temps. Notre ondelette "mère" nous fournit des petites ondelettes pour détecter des changements rapides du signal sonore dans le temps, et des ondelettes plus longues pour avoir une bonne résolution en fréquence. D’un point de vue psychoacoustique, la transformée en ondelettes paraît être mieux adapté que les autres méthodes d’analyse-synthèse à l’analyse de signaux sonores non stationnaires, car elle privilégie l’aspect temporel à petites échelles et l’aspect de la fréquence à grandes échelles. Néanmoins, selon Kronland-Martinet et Grossmann, pour avoir une description plus détaillée en termes de fréquence, il est parfois convenable d’utiliser la transformée de Fourier à court terme (Kronland-Martinet & Grossmann, 1991). Dès nos jours, la méthode des ondelettes semble être une des plus efficaces et prometteuses de toutes les méthodes d’analyse-synthèse, mais "on peut conclure avec certitude qu’au sujet de l’analyse-synthèse il n’y a pas de panacée universelle et que chaque cas a son approche personnelle" (Kronland-Martinet & Grossmann, 1991). Un de nos buts dans ce chapitre sera l’étude des différentes méthodes développées pour représenter un signal sonore en partant des théories quantiques du son, et de discuter les avantages et les aspects problématiques de chacune.
L’apparition des techniques granulaires qui exécutent l’analyse-synthèse d’un signal sonore a été fondamentale pour l’exploration du domaine du timbre. "Cette exploration peut nous éclairer sur la perception et la compréhension du timbre; elle nous conduit à des modèles simplifiés permettant de réduire les données lors de la synthèse; elle utilise des modèles de transformation du son d’origine, soit afin de réaliser un traitement musical classique (par exemple, en variant indépendamment hauteur, durée, articulation et intensité) soit pour étendre les ressources du timbre (réorganisant à volonté les variations complexes extraites de l’analyse dans le but d’obtenir des sons riches et nouveaux)" (Risset, Wessel, 1982).
Avec l’exploration du domaine du timbre on est arrivé à la conclusion qu’il fallait effectuer une modélisation spectrale des sons pour connaître leurs caractéristiques psychoacoustiques essentielles et pour pouvoir effectuer ensuite une imitation ou une possible modification des sons à partir des modèles spectraux obtenus en utilisant différentes techniques de synthèse. La modélisation spectrale se fait avec l’analyse des sons au moyen de l’algorithme de la transformée de Fourier à fenêtre glissante, de ses variantes, et d’autres algorithmes qui ont été développés à partir de ceux-ci. Dès les années soixante, des compositeurs et chercheurs comme J.C. Risset se sont intéressés à la modélisation spectrale des sons instrumentaux. Risset a réalisé des expériences pour imiter des tons de trompette par synthèse additive (Risset, 1966), en faisant d’abord plusieurs analyses de Fourier successives du signal sonore pour essayer de décrire l’évolution de chaque partielle de la trompette. L’étude des sons de trompette lui a permis d’isoler une propriété qu’on peut considérer comme un modèle des sons cuivrés: la proportion d’harmoniques aigus du spectre s’enrichit avec l’intensité. Donc, si l’intensité change au cours d’une note, le spectre change aussi (Risset, 1966). La découvert de cette propriété et la création d’un modèle a permis l’accomplissement des sons cuivrés en partant d’autres techniques de synthèse qui n’ont pas besoin d’utiliser un grand nombre de données ni d’effectuer une analyse préalable à la synthèse. Ceci est le cas de la technique de Modulation de Fréquence, très efficace pour la commande de spectres dynamiques grâce au paramètre de l’index de modulation (Chowning, 1973).

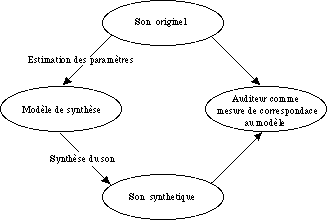
Figure 1.- Cadre conceptuel du processus d’analyse et de synthèse selon J.C. Risset et D. Wessel.
Jean Claude Risset a été l’un de premiers chercheurs à formuler l’idée d’une technique d’articulation sonore au niveau du micro domaine (c’est-à-dire, au niveau du timbre), en employant l’ordinateur comme outil de synthèse.
"L’ordinateur, utilisé comme outil de synthèse, permet d’élaborer à volonté la structure du son et de pousser le travail de composition jusqu’au niveau de la microstructure: le musicien qui ne se contente pas de composer avec des sons peut envisager de composer le son lui même" (Risset, 1985, 1991).
Les techniques d’analyse-synthèse ont eu une grande importance pour parvenir à l’articulation musicale du son dans le micro-domaine du timbre. Les compositeurs sont maintenant en mesure d’accéder au continuum de ce micro-domaine pour effectuer des métamorphoses et des transmutations de timbre, et pour pouvoir concevoir la création d’un espace de timbres "qui représenterait de façon adéquate les différences perceptives et qui pourrait servir comme une sorte de carte susceptible de guider dans sa navigation le compositeur qui s’intéresse à structurer des aspects du timbre" (Wessel, 1973). Toutefois, il faut tenir compte que cet espace de timbres n’est pas linéaire; pour cette raison, la recherche destinée à établir des règles pour une nouvelle syntaxe du son au niveau micro a été difficile, et encore aujourd’hui on travaille assidûment dans cet domaine peu aisé.
Les techniques d’analyse-synthèse ont été importantes et même essentielles pour explorer les propriétés spectrales du son et pour "composer" et transformer la micro-structure d’un son; cependant, l’utilisation de ces techniques afin d’effectuer la synthèse dans le macro-domaine sonore s’avère encore peu efficace, et lente du point de vue du calcul par rapport à certains techniques de synthèse traditionnelles (Additive, AM, FM, etc). D’autre part, quand on effectue l’analyse-synthèse d’un signal, la manipulation des données est parfois compliquée, car il est impératif de prendre en compte le facteur psychoacoustique. Il y a des éléments dans une analyse qui ne sont pas forcément importants pour la perception auditive, comme dans le cas du rapport des phases dans un signal sonore complexe. Cependant, selon Risset et Wessel "seulement les méthodes d’analyse-synthèse peuvent permettre des transformations sonores intimes" (Risset, Wessel, 1982), comme c’est le cas du contrôle fine des partiels d’un signal et la modélisation de son spectre au moyen d’un filtrage très précis. Davantage, ces méthodes rendent possible la réalisation d’une très riche variété de manipulations sonores: la réalisation d’interpolations entre différents timbres, divers types de synthèse croisée, des convolutions, des changements d’échelle temporelle d’un son sans changement de fréquence (ou changement de fréquence sans changement de durée), et beaucoup d’autres traitements de signaux intéressants. Or, seulement l’augmentation de la vitesse de calcul des ordinateurs actuels et une connaissance approfondie des phénomènes psychoacoustiques peuvent permettre aux chercheurs et aux compositeurs un travail plus souple et plus efficace au moment d’utiliser ces méthodes.
Le grand souci pour développer des algorithmes puissantes pour bien représenter un signal sonore dans le plan Temps-Fréquence a entraîné les chercheurs à créer des outils de synthèse qui sont toujours en fonction de l’analyse et des aspects psychoacoustiques de notre perception auditive. Le résultat de la re-synthèse doit alors être toujours contrôlé, et la reconstruction du signal doit souvent respecter certains rapports d’origine comme dans le cas des phases. Bien sur, sans contrôle on ne peut pas prévoir le résultat synthétique de la manipulation d’une analyse, mais comme on sait bien, quand il s’agit de créer des sons nouveaux, on agit souvent avec l’intuition et avec le principe expérimental "d’essai et d’erreur" ("trial and error"). Parfois même, des erreurs nous offrent des résultats plus intéressants que les produits d’une manipulation contrôlée. Enfin, ce que je voudrai exprimer c’est qu’il existe la possibilité de développer des outils d’analyse-synthèse qui ne sont pas forcément en fonction d’un résultat contrôlé. Ce serait le cas d’une idée que je n’ai pu développer et mettre en place. Que se passerait-il si l’on essayait d’avoir un contrôle stochastique sur les fenêtres d’analyse d’un signal sonore avant d’effectuer la re-synthèse?. Bien sûr, on perdrait le contrôle sur le rapport d’origine entre les phases, et on aurait comme résultat des produits sonores étranges au signal d’origine, mais ce résultat pourrait être intéressant du point de vue musical. J’ai été intéressé par la possibilité utopique de relier les techniques granulaires d’analyse-synthèse aux techniques de synthèse granulaire synchrones, presque synchrones et asynchrones, pour pouvoir travailler dans le micro et le macro-domaines du temps de façon simultanée. Apparemment, ceci constitue un paradoxe sans solution, car perdre le contrôle dans la re-synthèse signifie aller contre le principe même des techniques d’analyse-synthèse où l’intérêt est d’établir des conditions d’admissibilité au moment d’effectuer l’inversion de l’analyse pour pouvoir recréer le signal sonore d’origine. Néanmoins, on pourrait tout de même effectuer des transformations d’analyse traditionnelles (telles que la dilatation dans le temps que réalise un Vocodeur de Phase sur un son sans modifier sa fréquence) mais en introduisant des effets stochastiques sur les fenêtres d’analyse dans certains endroits de l’analyse des transformations, et en perdant donc le contrôle du résultat sonore sur certaines portions de la re-synthèse. Je ne sais pas si l’implémentation d’un contrôle discontinu et flexible des fenêtres d’analyse vaut vraiment la peine, mais la possibilité existe, et des effets sonores nouveaux et intéressants pourraient surgir de cette idée. Il faudra peut-être toujours accepter que les techniques d’analyse-synthèse servent seulement à travailler dans le micro-domaine du timbre et de façon contrôlée, et que pour relier les deux domaines du temps (micro et macro) il faudrait plutôt essayer d’utiliser les techniques granulaires formantiques (voir prochain chapitre), ou la synthèse granulaire traditionnel utilisée en même temps dans sa modalité synchrone, presque synchrone et asynchrone (voir deuxième chapitre). Toutefois, j’essaierai de développer davantage cette idée dans ce chapitre, et de parler aussi des différents essais réalises dans cette direction.
I.- L’algorithme de la transformation de Fourier et ses variantes.
1.- La transformation de Fourier.
Le timbre est un phénomène très complexe qui n'est pas facile à caractériser en comparaison de la fréquence et de l'intensité du son, car l'évolution du timbre d'un son a plusieurs variables qui changent d'une façon non-linéaire. Grâce au travail théorique de Hermann Von Helmholtz (théoricien du XIX siècle) on sait qu'un ton est constitué par une forme d'onde avec une enveloppe d'amplitude qui consiste en trois parties, le début, l'état stable, et la chute. Helmholtz parvient à la conclusion que les sons qui nous donnent une sensation de fréquence ont une forme d'onde régulière, et il se rend compte que la nature de la forme d'onde va déterminer le timbre d'un son (Helmholtz, 1877). Pour arriver à en savoir davantage sur la relation entre la forme d'onde et le timbre, Helmholtz utilise les recherches de Jean-Baptiste Fourier qui démontre qu'une fonction périodique peut être représentée comme l'addition d'une ou plusieurs sinusoïdes (sinus et cosinus) de différentes fréquences (c’est-à-dire, comme une série de Fourier). Chacun de ces sinusoïdes est caractérisé par sa fréquence, son amplitude et sa phase, et le changement dans le temps des trois paramètres (particulièrement les deux premiers) de chaque sinus va modifier la qualité de ce son, c'est-à-dire, le timbre. Helmholtz découvre aussi que n'importe quel signal (périodique ou non périodique) peut être défini par son amplitude par rapport au temps (forme d'onde), et par sa distribution d'énergie par rapport à sa fréquence (spectre). Grâce à un procédé mathématique complexe ("Transformée de Fourier") on peut obtenir aujourd’hui le spectre d'une forme d'onde, c'est-à-dire, ses différentes composantes en fréquence avec leurs caractéristiques qui vont déterminer la qualité du timbre.
Il faut bien faire la différence entre une "série de Fourier" et une "transformée de Fourier". Les "séries de Fourier" sont utilisées seulement pour l’analyse de signaux périodiques. Des tels signaux sont constitués par la superposition d’une onde sinusoïdale fondamentale et des divers harmoniques dont les fréquences sont les multiples entiers de la fréquence fondamentale. Les amplitudes de ces différentes fréquences sont calculées par de formules connues depuis le siècle dernier. Ces amplitudes sont appelées "coefficients de Fourier". Pourtant, pour analyser des signaux non périodiques on doit recourir à une intégrale de Fourier: la méthode utilisée consiste à représenter le signal étudié avec une superposition d’ondes sinusoïdales de toutes les fréquences possibles; les amplitudes associées à chaque fréquence forment une fonction de la fréquence ¶ que les physiciens appellent "spectre continu des fréquences du signal": c’est la transformée de Fourier du signal s(t), notée S(¶). Cette transformée est égale à l’intégrale pour toutes les valeurs du temps du produit du signal s(t) par la fonction e2ipft . On la calcule à l’aide de l’intégrale de Fourier:
S(¶) = Ú - • + • s (t)e2ipft
Une fonction et sa transformée de Fourier représentent deux aspects de la même information. La fonction met en évidence l’information sur le temps et cache l’information sur les fréquences, pendant que la transformée de Fourier révèle l’information sur les fréquences et cache l’information sur l’évolution temporelle. Pourtant, la fonction et sa transformée contiennent chacune l’information complète du signal: on obtient une transformée à partir de la fonction, et on reconstruit la fonction à partir de la transformée.
L’analyse de Fourier a aidé à comprendre certains phénomènes naturels (telles que le comportement de marées) en aidant à résoudre numériquement certaines équations qui au dernier siècle restaient réfractaires. Pour une sorte importante d’équations différentielles, la transformation de Fourier remplace une équation compliqué par une série d’équations simples (Burke, B. 1995). D’autre part, l’analyse de Fourier a été très utile pour le champ des télécommunications, car on peut déplacer les fréquences d’une voix vers d’autres fréquences, afin de la transmettre parmi bon nombre d’autres voix sur une seule ligne téléphonique.
2.- La transformée de Fourier rapide (FFT).
Bien que puissante, l’algorithme de la transformée de Fourier exige de longs et pénibles calculs mathématiques. Toutefois, en 1965 Cooley et Tukey ont établi un raccourci mathématique qui réalisait ces calculs en seulement quelque secondes à l’aide d’un ordinateur. Ils ont nommé leur algorithme "Fast Fourier Transform" (FFT). L’idée fondamentale de la FFT fut déjà pressentie par Carl Friedrich Gauss en 1805. Selon le mathématicien Gilbert Strang, du MIT, "l’algorithme qui a le plus changé notre société est la FFT. Des industries entières sont passées de la lenteur à la rapidité grâce à cette seule idée qui est de la mathématique pure" (Strang, G. 1993).
La FFT a eu un succès important à cause de son efficacité, et pour cette raison elle a été employée parfois dans des problèmes auxquels elle est inadaptée. Selon Meyer, la FFT ne convient ni a tous les signaux ni a tous les problèmes. Par exemple, si nous jouons une note basse, puis une note plus haute en fréquence, le spectre du signal est très diffus et il est très difficile d’y discerner les deux fréquences émises; de plus, l’ordre dans lequel sont joués les notes n’apparaît pas de façon claire dans l’analyse (Meyer, Jaffard, Rioul, 1987). L’analyse de Fourier se prête seulement à la résolution des problèmes linéaires pour lesquelles l’effet est proportionnel à la cause. La résolution des problèmes non linéaires est plus compliqué car il est difficile de prédire le comportement des certains systèmes dont une infime variation de paramètres peut bouleverser le résultat. D’autre part, l’inconvénient de l’intégrale de Fourier est qu’elle décompose le signal sur des fonctions sinusoïdales qui oscillent indéfiniment dans le temps, et nous savons que plus un signal est court dans le temps, plus il contient de composantes sinusoïdales d’amplitudes significatives (inversement un signal sinusoïdal infini correspond à une seule fréquence). Ce problème d’interaction entre le domaine du temps et le domaine de la fréquence a conduit à la création d’un algorithme de Fourier qui fonctionne dans un plan temps-fréquence comme on le verra tout de suite.
3.- La transformée de Fourier à fenêtre glissante ou transformée de Fourier à courte terme (STFT).
Avec la "Transformée de Fourier" on peut effectuer l'analyse d'un instant du comportement d'un signal sonore; alors, seulement s'il s'agit d'un signal régulier qui change très peu, on peut avoir une idée claire de son spectre (la structure de ses composantes spectrales), mais en réalité, presque tous les signaux sonores changent radicalement dans le temps, c'est-à-dire, que l'amplitude de leurs fréquences composantes (sinusoïdes) changent et transforment leurs timbres. On a mentionné au premier chapitre les critiques faites par divers physiciens de ce siècle sur la mauvaise utilisation de la transformation de Fourier pour analyser le son. Wiener en premier et après Gabor, ont constaté qu’il fallait considérer le facteur temps dans la décomposition d’une fonction quelconque par une transformée de Fourier.
"Pour pouvoir définir le timbre d'un son on doit considérer le nombre d'oscillations (fréquence), plus le devenir de ces oscillations dans le temps. Le problème pour décrire le spectre d'une note est que l'interaction entre la fréquence et le temps est extrêmement complexe" (Wiener, 1964).
D’autre part, Wiener s’est aperçu qu’il n’était pas possible d’analyser un son et d’avoir une précision dans le domaine de la fréquence et dans le domaine du temps de manière simultanée, et il a établi un comparaison entre ce phénomène et le principe d’incertitude de Heisenberg.
"Si on veut analyser une note qui dure un temps défini, on doit la décomposer en une bande d'oscillations harmoniques en mouvement, et il faut prendre en considération qu’aucune de ces oscillations ne pourra être prise comme la seule oscillation harmonique présente. Une précision temporelle aura comme conséquence un manque de précision des fréquences, et pour obtenir une précision des fréquences on ne devra pas tenir compte du domaine temporel" (Wiener 1964, pages 544, 545).
Gabor a été le premier à proposer une méthode d’analyse sonore dérivée de la physique quantique. Il s’est rendu compte qu’il fallait représenter le signal à la fois en fonction de la fréquence et du temps, car une bonne représentation en fréquence doit prendre en considération la durée des notes émises. Il a donc proposé un procédé plus efficace pour analyser un signal musical qui consiste à décomposer le signal en fonctions limitées dans le temps afin d’analyser des fragments indépendants (en utilisant l’analyse traditionnelle de Fourier). Ces fonctions constituent des "grains élémentaires" d’analyse, et la décomposition du signal à partir de ces fonctions constitue l’analyse temps-fréquence.
La théorie de Fourier - qui a été centrée sur l’aspect de la fréquence - n’avait son pôle complémentaire, le temps. Gabor a heureusement réuni les deux frères jadis séparés, et il a éliminé l’aspect continuiste de l’analyse de Fourier en introduisant le facteur temps. La représentation temps-fréquence d’un signal sonore est une représentation discrète et de caractère granulaire. Cette représentation met en jeu deux opérations réciproques: l’analyse et la synthèse. Au moyen de l’analyse, on décompose un signal sonore en fonctions élémentaires reliées à la transformation de Fourier; ces fonctions de type sinusoïdal dépendent seulement du paramètre de la fréquence, mais les coefficients que l’on affecte à chaque fonction élémentaire pour décomposer notre signal nous donnent une information directe sur les propriétés temporelles et de fréquence du signal. On calcule ces coefficients en faisant la somme en continu (l’intégrale) du produit du signal s(t) par la fonction élémentaire ya.b. (t) (Meyer, Jaffard, Rioul, 1987):
Ca.b. = Ú - • + • s (t) ya.b. (t) dt
L’analyse temporelle de Gabor découpe le signal de façon arbitraire en plages de longueur limitée. Ceci constitue une décomposition du signal sur des fonctions élémentaires ya.b. qui dérivent toutes d’une même "fonction fenêtre" y(t) par translation en temps et modulation en temps. Cette décomposition est appelée "La transformée de Fourier à fenêtre glissante", car, quand on a analysé un segment du signal, on fait glisser la fenêtre au long du signal pour analyser un autre.
Avec la conception quantique de Gabor sur le besoin d’avoir une représentation "granulaire" temps-fréquence du son, et l’application ultérieure de la transformée de Fourier à fenêtre glissante sur ordinateur (on l’appelle aussi transformée de Fourier à court terme ou STFT), on a résolu le problème majeur des physiciens (tels que Helmholtz) qui n’étaient pas capables de décrire l’évolution temporelle des composantes spectrales d’un son. Toutefois, l’idée d’avoir une fonction fenêtre de taille fixe pour effectuer l’analyse d’un son a impliqué de sérieux compromis. Quand la fenêtre d’analyse est étroite, on peut localiser les changements soudains du signal (tels que les pics et les discontinuités) mais on devient aveugle aux basses fréquences du signal (de période trop grande pour entrer dans la petite fenêtre). Par contre, quand la fenêtre d’analyse est large, on ne peut pas préciser l’instant où se produit un pic ou une discontinuité, car l’information est noyée dans la totalité de l’information qui correspond à la longueur de la fenêtre choisie. Ce paradigme indéterministe apparemment sans solution avait été déjà prévu par Wiener en 1925. On verra au cours de cet chapitre comment il va acquérir un rôle central dans le développement des différentes techniques d’analyse-synthèse, ainsi que les différentes idées qui ont été proposées pour essayer de le résoudre, mais à la fin, le principe quantique d’incertitude constituera toujours un obstacle pour connaître la réalité, et une résolution globale parfaite dans les domaines du temps et de la fréquence restera toujours irréalisable.
II.- Le Vocodeur de Phase.
Le Vocodeur de Phase a été à l’origine d’une série de techniques de codage de la voix crées pour essayer de réduire la quantité de data transmise dans la communication électronique de la parole. Son prédécesseur a été le Vocodeur à Chenaux (Channel Vocoder). Tous les Vocodeurs essaient de modeler leur signaux d’entrée - la parole en particulier - en une multiplicité de chenaux dont chacun décrit l’activité d’une région particulière du spectre du signal d’entrée. Le Vocodeur de Phase est un algorithme de traitement de signal qui appartient aux techniques d’analyse-synthèse. Avec cette méthode, un signal d’entrée peut être représenté par un modèle mathématique dont les paramètres changent au cours du temps, et ce modèle peut servir ensuite pour reconstruire le signal de façon identique ou bien être modifié pour créer un nouveau signal.
Dans le Vocodeur de Phase , le signal est modelé comme une addition des ondes sinus, et les paramètres à déterminer par l’analyse sont l’amplitude et la fréquence de chaque onde sinus et leur variance dans le temps. Le signal analysé ne doit pas avoir forcement des sinus avec un rapport harmonique; on peut analyser une grande variété de signaux musicaux tel que des sons d’instruments à vent, à cuivres, à cordes, la parole et quelques instruments de percussion. Néanmoins, certains sons de percussion et d’autres signaux sonores avec des caractéristiques de bruit ne sont pas bien représentés par une addition des ondes sinus. Ces signaux peuvent être parfaitement bien reconstruits par le Vocodeur de Phase, mais si l’on veut modifier l’analyse avant la re-synthèse, on ne peut pas prédire le résultat.
1.- L’interprétation d’une banque de filtres.
Il y a deux façons différentes et complémentaires d’envisager le Vocodeur de Phase (équivalentes du point de vue mathématique); la première est une interprétation d’une banque de filtres et la deuxième une interprétation de la transformation de Fourier (Dolson, 1986). Dans la première interprétation on a une banque de filtres fixe de type bandpass avec la sortie de chaque filtre représentée comme une amplitude et une fréquence qui varient dans le temps (Figure 2). Les filtres ont tous la même forme de bande, la même réponse de fréquence, et la même phase linéaire. D’autre part, les fréquences centrales des filtres sont séparées de manière équidistante. Quand les filtres sont alignés en fréquence, chaque filtre extrait exactement un harmonique du signaux et la re-synthèse peut alors être comprise comme une banque d’oscillateurs d’onde sinus où la variation d’amplitude et de fréquence de chaque oscillateur est contrôlée par les sorties de filtres correspondantes .
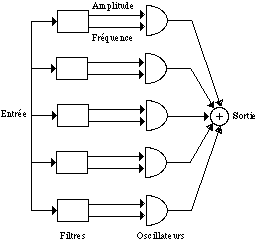
Figure 2.- L’interprétation d’une banque de filtres (Dolson, 1984).
Il faut tenir compte qu’avec les sons inharmoniques et polyphoniques on a besoin d’un plus grande nombre de filtres pour représenter les signaux sonores, car les partiels ne sont pas écartés de manière équidistante, et on a toujours besoin d’avoir un filtre pour chaque partiel pour bien représenter ces signaux. Si on n’a pas de filtres suffisants, différents partiels peuvent agir entre eux dans un seul filtre, et on perd l’information sur la fréquence individuelle de chaque partiel. En plus du nombre de filtres, il nous faut aussi déterminer la réponse en fréquence des filtres (ou largeur de bande). Avec une réponse de fréquence pointue (petite largeur de bande) le filtre mettra longtemps à répondre aux changements du signal d’entrée, mais on aura une définition en fréquence plus fine car il n’y aura pas d’interaction possible entre les partiels des différents filtres. Par contre, avec une largeur de bande plus large on aura une réponse de temps plus rapide, mais avec un chevauchement des fréquences entre les filtres bandpass qui sont voisins. Nous retrouvons ici le paradigme d’incertitude inhérent à la représentation d’un signal dans le plan temps-fréquence; on ne peut pas avoir une bonne définition globale du signal, il faut donc choisir et établir un compromis entre une bonne définition de fréquence et une bonne définition de temps. L’interprétation d’une banque de filtres privilégie le domaine de la fréquence. Cette vision est dans un certain sens continuiste, car elle envisage surtout la représentation des signaux périodiques plutôt statiques. Pour comprendre comment fonctionne le Vocodeur de phase avec des signaux non périodiques, il nous faudra considérer la deuxième interprétation qui est beaucoup plus puissante, reliée aux techniques d’analyse-synthèse qui ont une conception "granulaire".
2.- L’interprétation de Fourier.
Cette interprétation de l’analyse du Vocodeur de Phase consiste en une succession des transformées discrètes de Fourier de durée limitée et chevauchées (Figure 3). Ici, le Vocodeur de Phase se déplace dans le temps en prenant des "photos" du spectre qui évolue, et pour la re-synthèse, il prend la transformée discrète de Fourier inverse de chaque "photo" spectrale en chevauchant les signaux finis résultants et en les additionnant à nouveau (Dolson, 1984). Dans l’interprétation d’une banque de filtres, l’accent est mis sur la succession temporelle des valeurs de magnitude et de phase (fréquence) d’une seule bande de filtre. Par contre, l’interprétation de Fourier met l’accent sur les valeurs de magnitude et de phase de toutes les différentes bandes de filtres à un certain moment dans le temps (Figure 4).
Dans l’interprétation de Fourier, il faut tenir compte de la forme de la fenêtre d’analyse car l’opération de fenêtrage barbouille le spectre du signal. Le barbouillage augmente quand la taille de la fenêtre devient plus petite. La fonction fenêtre a le même rôle que la réponse du filtre dans l’interprétation du Vocodeur de Phase d’une banque de filtres. Une petite fenêtre est équivalente à une réponse du filtre plus lente (une grande largeur de bande du filtre), et donne une bonne définition en temps mais une mauvaise définition en fréquence, alors qu’une fenêtre plus longue est équivalent à une réponse du filtre plus net (une petite largeur de bande du filtre) et donne une bonne définition en fréquence mais une mauvaise définition en temps. L’interprétation de Fourier souligne le coté temporel mais aussi l’aspect de la fréquence, car on peut choisir la taille de la fenêtre et l’écartement entre les fenêtres d’analyse. Disons que cette interprétation est plus souple que l’interprétation d’une banque de filtres, car elle fonctionne mieux dans le deux sens. Cette interprétation utilise l’algorithme de la transformée de fourier à court terme (STFT), c’est-à-dire, une transformée de Fourier à fenêtre glissante, et comme on l’avait déjà vu, la taille de la fenêtre va jouer un rôle décisif pour l’analyse du signal. Le grand inconvénient est que la taille de la fenêtre est fixée une fois pour toutes, et qu’on ne peut donc avoir au même temps une bonne résolution dans le deux domaines (temps et fréquence). Quoi faire pour résoudre ce problème?. On verra dans ce chapitre comment certaines techniques ont essayé de modifier la taille de la fenêtre au cours du temps, ou d’avoir différents types de grains d’analyse, certaines pour trouver une bonne résolution en fréquence et d’autres pour trouver une bonne résolution en temps.
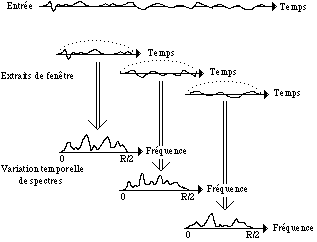
Figure 3.- L’interprétation de la transformation de Fourier (Dolson, 1984).
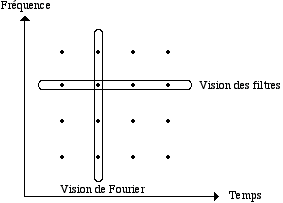
Figure 4.- Interprétation d’une banque de filtres vs l’interprétation de la Transformation de Fourier.
3.- Applications.
La tache principale du Vocodeur de Phase est la séparation entre l’information temporelle et l’information spectrale, en divisant le signal en une série de bandes spectrales qui évoluent dans le temps. Cette stratégie réussit seulement quand le signal de chaque bande évolue lentement. S’il y a plus d’un partiel dans la bande ou un changement brusque de l’amplitude ou de la fréquence, alors le Vocodeur de Phase est mal adapté pour analyser un signal. Un autre problème trouvé avec cette technique est que même si le signal de sortie contient des composantes sinusoïdales avec des amplitudes et des fréquences appropriées, les phases de ces composantes ne coïncident pas toujours avec celles du signal d’entrée. Parfois cet effet n’est pas audible, mais quand il agit sur le signal, il devient plus réverbérant que le signal d’origine (Moore, 1990).
Le Vocodeur de Phase a été utilisé depuis les années soixante-dix pour analyser des tons instrumentaux et déterminer l’évolution de leurs partiels. Ces recherches ont contribué à la connaissance des phénomènes psychoacoustiques sur la perception du timbre (Grey et Moorer, 1977). Cependant, l’intérêt principal de cette technique s’est centré sur la transformation des signaux sonores dans le domaine de la musique. Les opérations qui ont été le plus utilisées sont la dilatation/contraction en temps, la transposition de fréquence, et le filtrage temporel des fréquences, mais on a aussi développé d’autres transformations du signal telles que la synthèse croisée .
a) La dilatation/contraction en temps d’un signal.
Changer la durée d’un son est une des techniques électroacoustiques les plus utilisées; elle est comparable à l’utilisation de la dilatation et de la contraction des motifs mélodiques et rythmiques dans la composition musicale. Le changement de durée d’un signal sonore a été restreint au début à l’utilisation des premiers disques et des premiers magnétophones. Le procédé était simple: on changeait la vitesse du disque ou de la bande magnétique. Avec les premiers ordinateurs, on pouvait effectuer le même effet en changeant le taux d’échantillonnage d’un signal, mais avec tous ces procédés, un changement de vitesse contribuait toujours aussi à un changement de la fréquence du son.
Le Vocodeur de Phase peut effectuer une variation temporelle d’un signal sonore sans modifier sa fréquence. Ceci est faisable, car on peut rapprocher ou écarter les tronçons d’analyse spectrale (transformées de Fourier discrètes) au moment de la re-synthèse (Figure 5). Le seule problème qu’on rencontre est que pour avoir un signal résultant sans aucun produit sonore indésirable il faut remettre en échelle les phases du signal original, et ceci peut parfois être compliqué. Il n’est pas obligatoire que le changement temporel du signal soit fixe; on peut faire varier la dilatation ou la contraction d’un son dans le temps de façon non linéaire (Figure 6).
On a discuté dans le premier et le deuxième chapitres les techniques granulaires qui n’utilisent pas une analyse préalable du signal sonore. Ces techniques ont développé l’idée de dilatation et de contraction du son sans changement de fréquence depuis 1946 avec la construction du mécanisme de Gabor "Kinematical Frequency Converter" basé sur un projecteur modifié du film de 16-mm avec une piste sonore optique (voir premier chapitre). Otis, Grossmann et Cuomo ont réalisé la technique de granulation temporelle sur ordinateur à l’Université d’Illinois depuis 1968 mais avec certains problèmes dus à l’absence d’enveloppes (voir deuxième chapitre). Donc, la technique avait déjà été exécutée par d’autres moyens, qui cependant ne considéraient pas une bonne reconstruction du signal. Il faut reconnaître que dans ce sens là, le résultat du Vocodeur de Phase est plus propre malgré la difficulté de remettre les phases en échelle. Toutefois, l’avantage de la granulation temporelle effectuée par des techniques granulaires qui ne font pas une analyse préalable est qu’on n’a pas besoin d’effectuer un long calcul, ce qui donne la possibilité d’effectuer les transformations sonores en temps réel en utilisant des ordinateurs peu puissants. D’autre part, avec ces techniques, on sait préalablement qu’on n’aura pas une certitude totale du résultat car on ne contrôle pas les phases; donc, on a une approche beaucoup plus libre et souple pour contrôler les grains (voir deuxième chapitre). Il est curieux que des techniques d’analyse-synthèse comme le Vocodeur de Phase n’aient pas envisagé d’avoir un contrôle stochastique des fenêtres d’analyse, même s’il y a une perte de contrôle sur la phase.
D’autres techniques d’analyse-synthèse réalisent le changement d’échelle temporelle d’un signal avec certains différences d’approche. Certaines par exemple, sont plus efficaces pour remettre les phases en échelle, comme c’est le cas de la technique de Jones et Parks (1988) qu’on discutera dans ce chapitre.
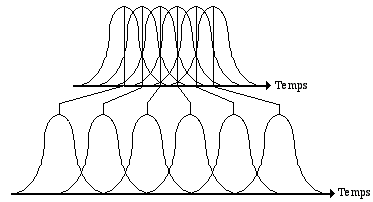
Figure 5.- Façon classique de déployer les grains dans le temps (Arfib, 1991).
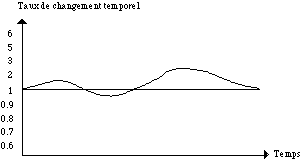
Figure 6.- Variations du changement temporel d’un signal.
b) Transposition de fréquence sans changement de durée.
Le fait de pouvoir modifier la durée d’un son sans l’altération de sa fréquence nous donne la possibilité de modifier sa fréquence sans altérer sa durée. Si on veut transposer d’une octave par exemple, il suffit de dilater deux fois dans le temps et puis jouer le son deux fois plus vite (doubler son taux d’échantillonnage). Ceci permet d’ajuster l’accordage d’un son, mais si la transposition est trop grande, on a une déformation du timbre car elle change la structure spectrale du son. Avec la parole ce phénomène est très palpable parce que les régions formantiques sont modifiées et le sens du langage devient incompréhensible (quand la transposition est d’une octave ou plus). Toutefois, selon Dolson (1984) on peut utiliser un algorithme qui déforme l’enveloppe spectrale pour lui rendre sa forme original au moment d’effectuer la lecture du son à une vitesse différente.
Avec la synthèse granulaire traditionnelle on a réalisé des expériences de transposition sans changement de durée, mais en général on effectue en même temps des changements d’échelle temporelle. On décide le taux de changement temporel en choisissant le temps absolu de synthèse, et ensuite on transpose les grains. Avec le programme SAM de Barry Truax sur le processeur DMX-1000, on peut même avoir plusieurs transpositions de grains simultanées, ce qui donne un effet semblable à un harmoniser (Voir chapitre 2). Mis à part le problème de la reconstruction de phases et des subséquents effets de modulation, la transposition dans ces techniques se fait très bien.
c) Filtrage temporel des fréquences.
En général, toutes les techniques d’analyse-synthèse sont capables d’effectuer un filtrage temporel des fréquences. Dans le cas du Vocodeur de Phase, si on considère l’interprétation d’une banque de filtres, il est clair qu’on peut éliminer certaines bandes de filtre ou augmenter l’amplitude d’autres bandes dans l’analyse, et ensuite synthétiser le nouveau signal transformé. Dans ce sens-là, le Vocodeur de Phase est très proche de la synthèse substractive et de la synthèse additive. On peut utiliser le filtrage temporelle des fréquences pour se débarrasser de certains types de bruit dans le signal d’entrée en effectuant l’élimination de certaines bandes qui ont une amplitude très petite, pour supprimer toutes les harmoniques paires ou impaires, pour supprimer un nombre fini d’harmoniques, pour supprimer une bande de fréquence bien précise, pour rehausser ou atténuer des régions du spectre en fonction de la dynamique du signal, etc. Ces opérations peuvent se situer dans le temps à des instants bien précis et varier sans contrainte. Une bonne implémentation du Vocodeur de Phase, particulièrement efficace pour réaliser différents types de filtrage, est le Super Vocodeur de Phase (SVP) développé à l’IRCAM (Depalle, Poirot, 1991), qui est devenu ensuite un logiciel plus sophistiqué par son interface graphique (AudioSculpt). Ce dernier logiciel (Figure 7) peut agir avec le logiciel PatchWork, qui est utilisé pour le contrôle des paramètres.
Le filtrage temporel des fréquences est une modalité du Vocodeur de Phase et d’autres techniques d’analyse-synthèse véritablement puissantes car on peut sculpter le son d’une manière très fine. Ceci constitue à mon avis la modalité la plus idiomatique des techniques d’analyse-synthèse pour transformer le son. Avec la synthèse granulaire sans analyse préalable il n’est pas possible d’effectuer ce type de transformations. Pour réaliser un filtrage précis il faut recourir à d’autres techniques.
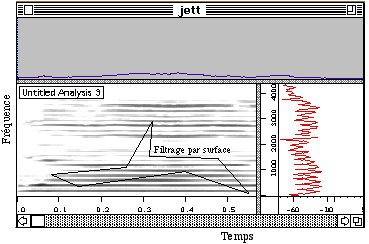
Figure 7.- Analyse spectrale d’un signal sonore réalisé par le Vocodeur de Phase AudioSculpt développé à l’IRCAM. Avec ce logiciel on a la possibilité d’effectuer différents types de filtrage temporel. Ici on réalise un filtrage par surface. On dessine la surface à filtrer sur le spectre temporel et on donne une valeur de changement d’amplitude en dB positive ou négatif qui va affecter les fréquences comprises dans la surface.
d) Synthèse croisée.
L’interprétation de Fourier du Vocodeur de Phase rend possible l’utilisation des spectres discrets de Fourier d’un signal pour modeler de façon dynamique les spectres discrets d’un autre signal. Ceci peut se faire avec la multiplication de l’analyse FFT d’un son par l’enveloppe spectrale d’un autre son, qui est parfois estimé par une analyse linéaire prédictive (LPC). On peut aussi réaliser une modulation en anneau (ou convolution en fréquence) entre les deux spectres. Toutes ces opérations peuvent être considérées comme une synthèse croisée entre deux signaux sonores.
Le fait d’avoir une conception discrète de l’analyse dans l’interprétation de Fourier nous permet la modification des paramètres de la synthèse croisée dans le temps. De cette manière on peut déterminer à quel moment on souhaite avoir un croisement entre deux sons.
III.- Granulation temporelle d’un signal par analyse-synthèse avec alignement des phases.
On a vu qu’avec le Vocodeur de Phase on peut trouver des problèmes pour la reconstruction des phases lorsqu’on effectue un changement temporel d’un signal sonore. Jones et Parks (1988) ont proposé une méthode pour effectuer la modification temporelle d’un son en extrayant des grains du signal et en récombinant ensuite les grains en alignant leur phases. L’extraction des grains se fait en multipliant chaque échantillon du signal par une fonction fenêtre .
Selon Jones et Parks, on peut décomposer un signal sonore en une série de grains et ensuite le reconstruire avec précision si les fenêtres sont choisies de telle façon que leur addition soit égale à l’unité à chaque point. Le but de la technique de Jones et Parks est d’affecter la reconstruction du son en écartant les grains, ou en comprimant les grains. Pour une compression par un facteur deux par exemple, on se débarrasse des grains pairs ou impairs et on rapproche ensuite les grains qui restent. Pour dilater un son, on effectue d’abord un chevauchement des grains, et ensuite on les écarte. Le problème trouvé avec cette technique est qu’après la transposition temporelle des grains, les phases dans leurs bords peuvent ne pas être identiques, et leur subséquente addition peut produire une interférence destructive qui causerait des battements (Jones, Parks 1988). Un chevauchement d’amplitudes de fenêtres qui n’additionnent pas l’unité pourrait aussi produire des battements non voulus. Pour résoudre ces problèmes, on a effectué l’ajustement de la localisation du commencement des fenêtres (au moyen d’un algorithme puissant) pour que le chevauchement de grains soit en phase. Dans ce cas, l’écartement entre les fenêtres n’est plus égal.
La technique de Jones et Parks et très flexible car elle permet que la durée des fenêtres, les locations nominales du commencement , et le nombre de grains à être chevauchés, soient complètement indépendants les uns des autres. En outre, cette technique fonctionne bien avec des signaux non périodiques et bruités. Pour cette raison, elle paraît plus puissante que le Vocodeur de Phase pour la réalisation des opérations de dilatation et de compression d’un signal dans le temps. D’autre part, avec cette technique on peut aussi réaliser des transpositions du signal; des combinaisons de segments entre deux signaux sonores différents; on peut l’appliquer aussi sur différentes bandes de fréquence en créant plusieurs chevauchements de grains d’un segment du signal avec un contenu de fréquence différent, en réalisant un filtrage bandpass du signal avant d’effectuer le fenêtrage. Certains des ces grains peuvent alors être éliminés sélectivement pour obtenir un effet "d’évaporation" décrit par Roads en 1985 (Jones, Parks 1988).
Pour la modification temporelle d’un signal il faut faire attention à la durée des grains choisie. Pour la parole, 20 msecs constitue la limite inférieure, car au-dessous, elle devient incompréhensible; d’autre part, on peut avoir des problèmes d’un manque de synchronisation des grains avec des durées inférieures à 35 msecs. Pour des grains plus longs, la synchronisation des phases n’est pas tellement importante et peut être omise. La forme de la fenêtre ne semble pas avoir une grande importance. Toutefois, les fenêtres triangulaires sont très adéquates pour obtenir de bons résultats. Cette technique à été exécutée en temps réel par Jones et Parks avec l’appui d’un microprocesseur TMS32010.
IV.- Granulation par analyse-synthèse de type Gabor.
On a étudié dans le premier chapitre la théorie quantique de la représentation granulaire d’un signal dans le plan temps-fréquence de Gabor. Dans cette théorie, il y a un rapport réciproque entre le signal temporel et sa représentation dans le plan temps-fréquence, et toute l’information est conservée si les valeurs sont données dans une grille rectangulaire (c’est-à-dire, une grille à intervalles réguliers d’espace dans le domaine du temps et de la fréquence) (Figure 8). Gabor a travaillé avec des grains de type sinus (ou cosinus) modulés en amplitude par des enveloppes Gaussiennes et il a montré que pour ces grains il y a une aire limitée d’influence en temps et en fréquence. Cette notion a été développée plus tard avec le nommé reproducing kernel (noyau reproduisant). Gabor a aussi parlé du principe d’incertitude au moment de définir le plan temps-fréquence. Quand on fait une analyse STFT d’un signal, au moment de reconstruire le signal avec une re-synthèse, on aura toujours des effets flous, car chaque grain de reconstruction a sa propre transformation de Gabor dans un domaine temps-fréquence limité, et le noyau reproduisant brouille l’image de la transformation. Ce phénomène est inévitable, et la seule chose à faire est d’essayer de trouver des moyens pour réaliser des analyses qui ne donnent pas trop d’artefacts au moment de la reconstruction du signal (Arfib, 1990).
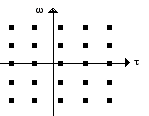
Figure 8.- Grille d’analyse de la transformée de Fourier à court terme (STFT). wo et to sont des nombres réels qui dépendent du choix de la fenêtre.
Certains chercheurs comme Daniel Arfib ont beaucoup travaillé avec les techniques d’analyse-synthèse qui découlent de la représentation granulaire de Gabor. Ils ont rencontré des problèmes occasionnés par le principe d’incertitude, et malgré ceci ils ont essayé de trouver des moyens pour améliorer ces techniques. Il y a toujours des variations très subtiles entre les différentes approches des techniques d’analyse-synthèse pour résoudre le problème d’une bonne reconstruction du signal et par rapport aux transformations qu’on réalise au moment de la re-synthèse. Toutefois, il est important d’analyser ces différences et de voir jusqu’où on peut aller dans le domaine des techniques granulaires d’analyse-synthèse. Je vais maintenant aborder la technique de type Gabor développée par Daniel Arfib (1990, 1991) et la comparer avec les autres techniques.
1.- Avantages et désavantages d’une analyse de type Fourier.
L’analyse de Fourier à court terme est utile pour avoir une information sur les phases du signal et pour pouvoir les reconstruire au moment d’effectuer la re-synthèse. Toutefois, un des problèmes de cette analyse est que les largeurs de bande sont fixes; les axes verticales de l’échelle de fréquence sont linéaires et donc, les octaves de sons harmoniques ne sont pas bien représentées. La perception psychoacoustique du timbre est de type logarithmique (Moles, 1964). Or, pour avoir un bon outil d’analyse pour la réalisation des recherches sur la perception du timbre, d’autres méthodes sont parfois plus appropriées, comme dans le cas des ondelettes. Néanmoins, quand on veut regarder en détail les composantes spectrales des sons inharmoniques complexes, l’analyse de Fourier peut être plus efficace que la transformation par ondelettes. D‘autre part, malgré ses caractéristiques non logarithmiques, selon Arfib les programmes qui utilisent la transformation de Fourier sont bien adaptés pour les méthodes de synthèse par analyse.
2.- L’effet des paramètres dans l’analyse-synthèse de type Gabor.
D’abord, il faut exposer les effets déterminants de certains paramètres au moment de réaliser une analyse de Fourier à court terme. La fenêtre d’analyse qui est multipliée par un segment du signal va toujours affecter le résultat de l’analyse, mais on doit forcément utiliser une fenêtre, car si on n’en a pas, l’effet sur l’analyse empirerait. Les fenêtres le plus utilisées sont Hamming, Hanning et Blackmann. Cependant, Gabor avait décidé d’utiliser une fenêtre de Gausse car elle est bien localisée en temps et en fréquence et parce que sa transformation de Fourier n’altère pas sa forme. La taille de la fenêtre et l’intervalle de temps entre les FFT prises sont aussi deux facteurs importants. On a déjà parlé de l’effet de la taille de la fenêtre, qui a une influence décisive sur l’analyse; une longue fenêtre privilégie une résolution en fréquence et une petite fenêtre privilégie une résolution en temps. D’autre part, l’écartement entre les différentes FFT’s fait varier la résolution de la vue de l’analyse. Un bon compromis pour une analyse est de choisir une FFT de 1024 points avec une fenêtre de type Hanning.
Pour effectuer une analyse de type Gabor, on applique des fenêtres écartées de manière équidistante à un son quelconque et on obtient une série des grains. Pour acquérir une bonne reconstruction du signal sonore au moment de la re-synthèse, l’addition des fenêtres d’analyse successives doit être égale à 1. La forme de la fenêtre va déterminer la distance entre les fenêtres; si notre fenêtre est carrée la distance est égale à la largeur de la fenêtre; si notre fenêtre est Hanning, la distance doit être égale à la moitié de la durée de la fenêtre. Donc, avec une fenêtre Hanning de 1024 points, on doit utiliser un intervalle de temps de 512 échantillons.
3.- Transformations sonores musicales de type Gabor.
Il faut tenir compte que lorsqu’on réalise la transformation d’une analyse pour obtenir un son nouveau, le résultat ne ressemble pas à celui de l’analyse. "La transformation arbitraire d’une transformation légale est illégale, car la reconstruction granulaire d’une fonction bi-dimensionnelle donne un signal dont la transformation est différente de la fonction initiale" (Arfib, 1991). Néanmoins, selon Arfib on peut se rapprocher beaucoup, et même si le résultat est inattendu, il peut être musicalement intéressant. Ici, je reviens à ce dont j’ai parlé en début de chapitre. La préoccupation constante des techniques d’analyse-synthèse est de trouver un moyen d’effectuer des transformations légales, et ceci est impossible. On devrait peut-être dévier un peu l’attention et essayer de trouver des transformations intéressantes au niveau musical, même si on n’a pas un contrôle absolu sur le résultat. En fait, Arfib se trouve parmi les chercheurs qui ont essayé de proposer des transformations intéressantes possibles, et en même temps il a cherché à minimiser les effets indésirables occasionnés par le noyau reproduisant .
a) La dilatation/contraction d’un signal dans le temps avec des grains de Gabor.
L’approche du changement temporel d’un signal en utilisant de grains de Gabor est très semblable à d’autres approches faites par des techniques d’analyse-synthèse telles que le Vocodeur de Phase , les ondelettes, la technique de Jones et Parks, etc. Le but de Daniel Arfib à été de créer une méthode qui fonctionne de manière indépendante de la nature de la source, et qui peut être exécutée par de petits ordinateurs (Arfib, 1991). Le problème principal trouvé est le même qu’avec le Vocodeur de Phase: on peut écarter les fenêtres d’analyse et effectuer ainsi une dilatation temporelle, mais on aura une mauvaise reconstruction des phases et le subséquent effet sonore, non voulu, d’un filtre en peigne. La solution donnée par Arfib est de multiplier les phases par le ratio intégral du changement temporel (ou taux du changement temporel) avant d’effectuer la transformation de Fourier inverse et additionner les nouveaux grains. Pour des ratios non intégrales, Arfib a trouvé le moyen de déduire la valeur du tournage de la phase pour chaque déplacement de fenêtre. Cette technique est plus pratique que l’algorithme utilisé par le Vocodeur de Phase, où on doit effectuer une FFT pour chaque point du signal afin de pouvoir suivre la reconstruction des phases (avec la technique d’Arfib on a besoin d’effectuer une FFT seulement tous les 128 points pour une FFT de 1024 points). L’autre différence est que le Vocodeur de Phase doit effectuer un filtrage bandpass du signal avant de le reconstruire.
a.1) Effets de la taille de la fenêtre sur le changement temporel de la parole.
Les expériences effectuées par Arfib avec la parole ont donné des résultats intéressants. En utilisant une fenêtre de taille 128 ou 256 points pour effectuer un changement temporel d’un taux de 8, on a obtenu une granulation rauque sur le timbre de la parole. Par contre, avec des fenêtres plus longues au-dessus de 1024 points (2048 et 4096), on a obtenu un effet de réverbération semblable à des échos successifs tellement proches qu’ils se fusionnent.
Quand on effectue une dilatation de la parole dans le temps, il faut savoir que si le taux de dilatation est excessif, la parole deviendra incompréhensible car la transformation déforme les consonnes au point que l’on ne peut plus les reconnaître. Une technique intéressante est d’affecter davantage les voyelles, et même si on affecte seulement les voyelles et on laisse les consonnes intactes, on aura une transformation intéressante du point de vue musical.
Les effets sonores de la fenêtre sur la re-synthèse peuvent être très intéressants du point du vue musical comme on l’a remarqué, alors, pourquoi n’a-t-on pas pu imaginer des transitions possibles entre l’effet de granulation rauque et l’effet d’échos réverbérants?. Il faudrait simplement changer la taille de la fenêtre dans le temps, et on pourrait ainsi effectuer des transformations de timbre très intéressantes. Je ne suis mathématicien et je ne peut pas savoir s’il est possible de modifier la taille de la fenêtre en gardant le rapport des phases, ou au moins, de minimiser des effets sonores indésirables avec un algorithme, mais j’imagine que ce doit être faisable.
b) Transposition de fréquence sans changement de durée avec des grains de Gabor.
L’effet ici est exactement le même qu’avec le Vocodeur de Phase (Voir Vocodeur de Phase). La différence principale est la manière d’effectuer le changement de l’échantillonnage du signal. Ici on interpole avec un filtre de réponse fini (FIR). On peut obtenir de mauvais effets de aliasing si on sous-échantillonne.
c) Filtrage avec convolution linéaire par FFT.
Le filtrage le plus commun et le plus simple est la réalisation d’une convolution circulaire sur le signal pour altérer les amplitudes données par l’analyse. Ceci se fait par une multiplication du fenêtrage du signal initial avec la réponse spectrale des filtres. Avec la convolution linéaire, on effectue cette même multiplication mais on prend seulement la moitié de la période du signal pour qu’il n’y ait pas un chevauchement entre ses différentes périodes.
d) Séparation Source-Résonance.
La voix humaine peut être décomposée en deux éléments essentiels qui ont un rapport direct. La source, constituée par les cordes vocales qui produisent des vibrations de différentes fréquences; et la boîte de résonance, constituée par la tête, la bouche et le nez, qui détermine l’enveloppe spectrale de la source par un filtrage formantique (Figure 9). Dans la musique par ordinateur, ce filtrage peut se réaliser à l’aide d’un filtre récursif de réponse impulsionelle infinie (IIR) ou par un filtre non récursif de réponse impulsionelle finie (FIR).
Pour réaliser une séparation source-réponse dans une granulation de signal de type Gabor, on doit séparer chaque grain en deux grains différents, l’un qui agit comme la source et l’autre qui agit comme le filtre résonateur. Les méthodes traditionnelles pour réaliser cette opération sont la prédiction linéaire (LPC) et le cepstrum. Avec une granulation de signal de type Gabor, l’opération qui sépare la source de la réponse est de type discret, car on peut affecter chaque paire de grains de l’analyse, et donc, on peut avoir des transformations qui changent de manière plus fine dans le temps.
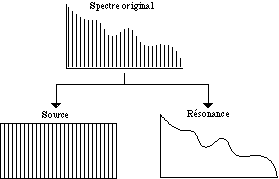
Figure 9.- Séparation entre source et résonance d’un signal périodique (Arfib, 1991).
Avec la séparation d’un signal en deux signaux granulaires différents on peut réaliser des transformations musicales très utiles, par exemple, on peut faire une transposition de la voix sans modifier sa durée et son enveloppe spectrale. Ceci est facilement réalisable car on doit seulement transposer les grains de la source et laisser les grains de l’enveloppe spectrale intactes. On résout ainsi le problème de la transposition sans changement de durée typique, où l’enveloppe spectrale est déformée à cause du changement du taux d’échantillonnage (voir vocodeur de phase). On peut aussi faire varier les deux spectres de façon souple et indépendante et avoir des effets de glissandi, ou d’une voix transformée quand on altère l’enveloppe spectrale. On peut aussi utiliser la source d’un son et la résonance d’un autre son et effectuer une synthèse croisée. La différence avec le Vocodeur de Phase sur ce point, est qu’ici on établit un croisement entre la moitié d’un signal et la moitié de l’autre, alors qu’avec le Vocodeur de Phase on fait une analyse LPC d’un signal et une analyse FFT d’un autre signal, et on effectue ensuite une convolution. La technique de Arfib est peut-être plus intéressante, car les deux signaux ont plus d’indépendance.
e) Modification des phases.
On peut modifier la valeur des phases après l’analyse et modifier ainsi le signal sonore. Par exemple, si on met toutes les valeurs des phases à zéro, on aura un effet de filtre en peigne au moment de la reconstruction du signal. On peut expérimenter avec d’autres valeurs mais il faut prendre en considération que lorsqu’on altère les phases d’un signal, on risque toujours de générer du bruit. D’autres effets possibles sont différentes variétés de réverbération et des effets chorales.
Théoriquement, on peut affecter la phase de chaque grain de façon indépendante. Ceci fait que l’on peut créer des modifications de phases qui varient dans le temps. De cette manière, on pourrait créer des effets qui apparaissent et disparaissent graduellement dans le temps, et des subséquentes variations du timbre. J’ignore si Arfib a envisagé cette possibilité.
VI.- Les Ondelettes.
"Les ondelettes sont des fonctions élémentaires ya..b très particulières; ce sont les vibrations les plus courtes et les plus élémentaires que l’on puisse envisager" (Meyer, Jaffard, Rioul 1987).
1.- L’invention des ondelettes.
A partir de la critique de Gabor à la théorie de Fourier et de sa conception sur la représentation du signal sonore dans un cadre bi-dimentionel temps-fréquence, on a développé des algorithmes reliés à la transformation de Fourier qui utilisent une fonction fenêtre pour analyser le signal par segments successifs. Des algorithmes de ce type tels que la transformée de Fourier à court terme (STFT) ont prouvé leur efficacité pour décrire l’évolution des partiels d’un son quelconque (Grey, Moorer 1978). Néanmoins, le fait d’être obligé de choisir une taille fixe pour la fenêtre d’analyse, a limité la résolution des analyses réalisées, car avec une fenêtre longue on obtient une bonne résolution des fréquences, mais on reste aveugle aux discontinuités du signal, et par contre, avec une fenêtre courte on obtient une bonne résolution des changements soudains du signal, mais une mauvaise résolution en fréquence.
Dans les années soixante, les géophysiciens utilisaient l’analyse de Fourier pour effectuer les recherches du pétrole sous terre. Ils envoyaient des vibrations dans la terre pour analyser les échos résultants. Les signaux de réflexion associés aux différentes couches souterraines interféraient entre eux, et il fallait les séparer pour accéder à des informations sur des couches de différentes épaisseurs. Dans les années soixante-dix, le géophysicien Jean Morlet a essayé d’utiliser l’analyse de Fourier à fenêtre pour séparer les différents signaux, mais cet algorithme n’était pas précis à cause de la taille fixe de la fenêtre qui donnait une mauvaise résolution globale dans le plan temps-fréquence. Morlet essaya alors de faire varier la taille de la fenêtre (en gardant le même nombre d’oscillations), en l’étirant ou en la comprimant comme un accordéon. Quand on étire la fenêtre, les oscillations se dilatent et les fréquences résultantes sont basses; quand on comprime la fenêtre, les oscillations sont aussi comprimées et les fréquences résultantes sont plus hautes. Morlet pouvait alors localiser les hautes fréquences avec les petites fenêtres et étudier les basses fréquences avec les fenêtres plus larges. Il nomma ces nouvelles fonctions ondelettes de forme constante pour les distinguer des fonctions de Gabor (qu’il appelait ondelettes de Gabor) et des ondelettes utilisées en géophysique (Burke Hubbard, 1995).
Dans les années quatre-vingt, Morlet a travaillé à côté d’Alex Grossmann pour affiner sa théorie. Ils ont trouvé qu’on pouvait transformer un signal en ondelettes et puis reconstruire exactement le même signal à partir des ondelettes. De plus, ils se sont aperçus qu’un grande avantage de cette technique était qu’une petite erreur ou une modification dans l’analyse n’était pas amplifiée de façon disproportionnée. Toutefois, leur méthode de reconstruction était plus lourde que celle de la transformation de Fourier, car ils avaient une transformée à deux variables (temps et fréquence), mais Morlet et Grossmann ont trouvé un moyen d’effectuer une reconstruction approximative par une intégrale simple (Grossmann & Morlet, 1985).
Au fur et à mesure que la recherche sur les ondelettes à évolué, beaucoup de chercheurs ont manifesté leur intérêt et ont contribué à l’invention de différents types de transformées et de différents types de "grains" élémentaires. Des nos jours, les ondelettes sont très utilisées pour analyser diverses types de signaux; elles sont surtout utilisées dans le champ de la vision, car elles servent à extraire le bruit d’un signal, à renforcer les détails d’une image floue, à la compression des images, à étudier des objets fractaux, etc.
2.- Utilisation des ondelettes pour l’analyse et la synthèse des signaux sonores.
a) Définition des ondelettes.
Les ondelettes sont des fonctions élémentaires ya..b. Il y a plusieurs familles d’ondelettes ya..b qui correspondent à des décompositions différentes; elles ont des propriétés différentes et permettent de faire des analyses différentes. Chaque famille d’ondelettes est générée par une seule ondelette mère y(t) dite analysante et définie par: y(t) = cos (5t) x e -t2/2
Les ondelettes de Morlet ont été construites à partir de l’ondelette analysante y par translation en temps et par contraction ou dilatation en temps.
On a vu au début de ce chapitre qu’avec l’algorithme de Fourier à fenêtre glissante on décompose un signal sonore sur des fonctions élémentaires ya..b. qui dérivent toutes d’une même "fonction fenêtre mère" y(t). Le procédé est très similaire à celui des ondelettes, mais la différence est qu’avec l’algorithme de Fourier on réalise cette décomposition par translation en temps et par modulation en temps. La fonction analysante (ou fenêtre d’analyse) de Fourier reste fixe, pendant que les fréquences analysées par la fonction changent (Figure 10). L’inconvénient de cette méthode est que si l’on a une fréquence trop basse et la fenêtre n’est pas assez large, la fonction ne peut plus reconnaître la fréquence du segment du signal analysé. Avec les ondelettes on n’a pas ce problème, car elles s’adaptent aux fréquences du signal en s’étirant ou en se comprimant, toujours en gardant le même nombre d’oscillations.
L’avantage principal des ondelettes sur la transformée de Fourier à court terme est la possibilité d’effectuer une analyse multirésolution, c’est-à-dire, une analyse à différentes échelles. Pour ce faire, on comprime ou on étire une ondelette mère selon la taille de l’intervalle que l’on veut étudier. Cette analyse agit comme un "microscope mathématique", car les ondelettes s’adaptent automatiquement aux différentes composantes du signal: les ondelettes larges donnent une image approximative du signal, tandis que les ondelettes étroites permettent de "zoomer" dans les détails. La possibilité d’avoir différents niveaux de résolution à différentes échelles (on utilise en général cinq niveaux de résolution, chacun étant deux fois plus fin que le précèdent) fait que l’on parle souvent d’octaves. Doubler la résolution équivaut à augmenter la fréquence des ondelettes par deux (d’une octave). Ceci peut être un avantage dans l’analyse musicale d’un signal; par exemple, quand on veut localiser correctement les intervalles d’octave dans une séquence harmonique. Toutefois, les ondelettes peuvent aussi décomposer un signal en choisissant d’autres fonctions élémentaires (ou "grains"). De cette manière, on peut effectuer des analyses pour détecter d’autres intervalles ou d’autres structures pré-définies.
Le désavantage des ondelettes par rapport à l’analyse de Fourier est que l’information sur les fréquences n’est qu’approximative; une ondelette n’a pas comme un sinus ou un cosinus une fréquence précise (Burke Hubbard, 1991). Toutefois, les ondelettes sont capables de ressortir les variations du signal et avoir en même temps une bonne approximation dans le domaine des fréquences, pendant que l’analyse de Fourier à court terme est incapable de faire les deux choses en même temps.
L’analyse par ondelettes associe à un signal réel une fonction qui dépend de deux variables: temps et échelle. La grille d’analyse des ondelettes (Figure 11) diffère donc de la grille d’analyse de la transformée de Fourier à court terme (STFT), car la fonction de la STFT dépende des variables: temps et fréquence. Dans la conception d’une banque de filtres (voir Vocodeur de Phase), les ondelettes peuvent être interprétées comme réponses impulsionelles de filtres Q-constantes (D¶/¶ = constante), et les grains élémentaires de la STFT comme des réponses impulsionelles de filtres avec une largeur de bande constante (D¶ = constante). Si l’on considère qu’une voix est équivalente à un filtre, avec les ondelettes la voix peut être définie par la sortie (output) du filtre avec sa réponse impulsionelle donnée par le grain correspondant. La largeur de bande des filtres dans une analyse par ondelettes va changer selon des grains, pendant que la largeur de bande des filtres dans la STFT sera toujours fixe. Par sa nature, la STFT tend à décomposer un signal arbitraire en composantes harmoniques (car les filtres sont équidistants et ont une largeur de bande fixe) tandis que la transformée en ondelettes a l’avantage d’être en mesure de choisir la fonction élémentaire (ou "grain") de décomposition.
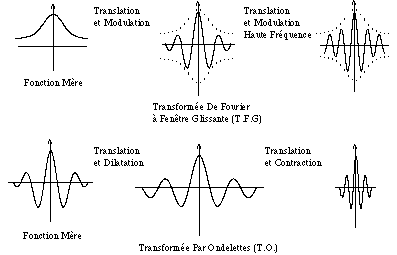
Figure 10.- La transformée de Fourier à fenêtre glissante (TFG) et la transformée en ondelettes (TO) sont deux méthodes de représentation temps-fréquence d’un signal qui consistent à le décomposer en somme des fonctions élémentaires y a.b.(t), qui dérivent toutes d’une même fonction "mère" y(t) par translation dans le deux cas, par modulation en temps (y a.b.(t) = y(t - b) x cos (2pat)) pour la TFG, et par contraction et dilatation en temps pour la TO. (Meyer, Jaffard, Rioul, 1987).
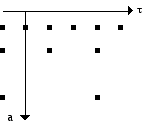
Figure 11.- Grille de la transformée en ondelettes, où a0 et t0 sont des nombres réels qui dépendent du choix de l’ondelette.
b) Propriétés de la transformée en ondelettes.
"La transformée en ondelettes est une fonction S(a, b) qui associe aux paramètres a et b la valeur du coefficient Ca.b. de l’ondelette ya..b. dans la décomposition du signal. La quantité b est le paramètre de localisation temporelle, tandis que 1/a est le paramètre de fréquence. Le coefficient Ca.b. est égal à la somme en continu du produit du signal par l’ondelette ya..b." (Meyer, Jaffard, Rioul, 1987).
b.1) Coefficients.
Donnons quelques propriétés des coefficients dans la transformée en ondelettes:
Le coefficient Ca.b. est très petit dans les zones où le signal analysé s(t) est très régulier. Un intervalle constant du signal donne un coefficient nul. Les nombres nuls concentrent l’information du signal dans quelques coefficients. Cela peut être utile pour la compression de sons ou d’images, pour obtenir une plus grande vitesse de calcul, et pour l’analyse des signaux qui ont des singularités ou des discontinuités.
Les grains élémentaires en général ne sont pas orthogonaux (Kronland-Martinet, 1991), et dans ce cas, les coefficients obtenus avec le même type de calcul ne permettent pas de reconstruire le signal original. Néanmoins, la reconstitution du signal dans une base non orthogonale est possible si l’on mesure l’erreur au moment de reconstruire le signal. En outre, dans certaines circonstances imposées sous les grains on peut construire des bases orthonormales qui correspondent à la grille d’analyse de la transformée en ondelettes préalablement définie. L’orthogonalité peut être utile car elle fournit une reconstruction parfaite du signal originel en évitant la redondance au cours de l’encodage. D’autre part, avec une transformation en ondelettes orthogonales, signal et bruit peuvent se dissocier, car on comprime l’énergie du signal en un nombre assez restreint de gros coefficients. L’énergie du bruit blanc est dispersée sur toute la transformée et donne des petits coefficients qu’on peut éliminer.
Le seule désavantage des coefficients des ondelettes est qu’ils sont plus difficiles à interpréter que les coefficients de Fourier. "Les coefficients de Fourier ne sont pas que des concepts, ils sont physiques et réels comme une table; en revanche, les ondelettes n’ont pas d’existence physique" (Meyer, 1992).
b.2) Linéarité.
La transformée en ondelettes de même que la STFT sont linéaires. Cette propriété est très utile car la transformée de l’addition des signaux est égale à l’addition de leur transformées. Ceci est convenable pour l’analyse des signaux polyphoniques (Kronland-Martinet, 1991).
b.3) Conservation de l’énergie.
L’énergie (la valeur moyenne du carré de l’amplitude) ne change pas. Il s’ensuit qu’on peut transformer un signal en ondelettes et puis reconstruire exactement le même signal à partir des ondelettes.
b.4) Comportement de la transformée sous translation et dilatation du signal.
La transformée en ondelettes d’un signal change d’une manière simple si le signal est déplacé ou remis en échelle (elle est covariante sous translation en temps). La STFT est covariante sous translation en fréquence mais elle n’est pas covariante sous translation en temps.
c) Les ondelettes et la perception auditive.
La transformation en ondelettes est bien adaptée pour effectuer des analyses acoustiques des signaux sonores car elle peut se servir des échelles logarithmiques pour les "grains" d’analyse. A partir des études sur le fonctionnement de l’ouïe, on a constaté qu’elle réalise un traitement du signal sonore de type logarithmique. Le son voyage à travers le canal externe de l’oreille et fait vibrer le tympan, celui-ci, transmet ces vibrations aux osselets (marteau, enclume et étrier), l’étrier transmet la motion à une membrane, ce qui cause la propagation de l’onde dans le fluide de la cochlée qui stimule les petites poils de la membrane basilaire. Les nerfs attachés à ces poils transmettent une stimulation au cerveau. Quand une fréquence périodique sinusoïdale audible arrive dans l’ouïe interne, elle excite les extrémités des nerfs dans des endroits de la membrane qui sont proportionnels à la fréquence du ton (Roederer, 1975). Quand des impulsions élémentaires (impulsions qui font intervenir toutes les fréquences) arrivent à l’ouïe interne, chaque point de la membrane basilaire décrit une courbe en fonction du temps qui est une ondelette. Cette ondelette se dilate lorsque la fréquence augmente, ce qui semble mieux correspondre à une modélisation par ondelettes qu’à une modélisation par la transformée de Fourier à fenêtre glissante (puisque celle-ci fait intervenir des modulations). La propriété de dilatation des ondelettes donne le résultat d’une modélisation psychoacoustique de la réponse à l’excitation impulsionelle sur divers points de la membrane (Meyer, Jaffard Rioul, 1987).
Les caractéristiques des ondelettes ont conduit certains chercheurs à les utiliser pour de tâches en rapport avec la perception psychoacoustique. Ellis et Vercoe (1991) ont développé un modèle de séparation auditive basé en ondelettes. Ils ont utilisé une transformée constante Q car elle simule la transformation en fréquence effectuée par la cochlée. Cette analyse consiste en une banque de filtres bandpass (des filtres FIR) où chaque filtre a une largeur de bande légèrement différente. La largeur de bande des filtres augmente avec une montée de fréquence, et on a comme conséquence une analyse de type logarithmique. Ceci est pratique quand on veut séparer de basses fréquences (qui ont une bonne définition en fréquence) des composantes spectrales aiguës (qui ont une bonne définition en temps mais mauvaise en fréquence). Cette technique est très efficace pour analyser la parole, puisque les filtres pour les hautes fréquences détectent la variation rapide des harmoniques et ils permettent aussi de détecter les régions formantiques malgré leur manque de résolution en fréquence. La transformée de Fourier à court terme avec ses filtres de largeur de bande fixe ne pourrait pas fonctionner pour séparer deux signaux sonores différents, car la réponse impulsionelle des filtres est la même dans tout le rang des fréquences.
d) L’analyse des signaux sonores.
La transformée en ondelettes est bien localisée autant dans le domaine du temps que dans le domaine de la fréquence. Ceci permet l’analyse des sons naturels de tout type avec une grande précision. L’analyse par ondelettes permet une interprétation physique des phénomènes sonores en termes de distribution d’énergie. Pour obtenir une représentation réaliste du modulos de la transformation, il est recommandable de séparer les composants positifs des composants négatifs pour éviter des battements de fréquence. Ceci n’est pas faisable avec une analyse de Fourier à courte terme. Un autre avantage de l’analyse par ondelettes est qu’elle permet une localisation en temps qui s’améliore au fur et à mesure que l’on progresse vers des petites échelles.
d.1) L’analyse musicale.
On a déjà mentionné que l’on peut construire des ondelettes adaptées à l’analyse de différentes structures d’intervalles de fréquence. Ceci peut être très utile pour détecter des motifs harmoniques dans des enregistrements de musique instrumentale. Par exemple, une ondelette avec deux chocs dans le domaine de la fréquence qui sont séparés d’une intervalle d’octave permet de détecter la récurrence d’octaves. Quand on analyse une séquence harmonique de différents intervalles avec une ondelette de ce type, l’énergie locale dans le plan temps-échelle est plus grande pendant les instants où le signal contient des octaves (Kronland-Martinet, 1988).
On peut utiliser les ondelettes pour la détection d’attaques de notes. Des essais de détection d’attaques ont été faits dans un contexte de transcription automatique (Foster et al 82). Crawford et Findlay ont proposé l’utilisation des ondelettes pour identifier l’attaque des notes des sons polyphoniques, et ils ont réalisé des expériences avec des instruments solo (Crawford, Findlay, 1996). L’analyse par ondelettes est très efficace quand on a différentes mélodies avec des timbres différents et dont les notes se chevauchent. On peut choisir une fonction élémentaire de décomposition basée sur une structure de demi-tons et savoir quel instrument a joué une note à un instant donné, puisque les ondelettes sont capables de détecter l’instant temporel en même temps que la structure spectrale des notes. Les ondelettes ont été aussi utilisées pour l’analyse fréquentielle du rythme (Leigh M. Smith, 1996). Leigh a employé la transformée en ondelettes continue (CWT) pour analyser le mouvement expressif des accents agogiques et dynamiques qui produisent de multiples signaux rythmiques à court terme et qui varient en amplitude et en fréquence sur différentes échelles temporelles. Cette technique permet de détecter des motifs rythmiques musicaux et d’étudier avec précision notre perception du rythme.
d.2) Estimation des paramètres.
Il est parfois utile d’extraire certains paramètres des signaux sonores qui décrivent des phénomènes physiques. La détection des composantes spectrales et de lois de modulation en amplitude (AM) et en fréquence (FM) servent pour simuler ensuit le signal par synthèse en utilisant des techniques additives et de Fréquence Modulée (Chowning, 1973). Il est possible d’estimer la fréquence des composantes spectrales en prenant la moyenne de la fréquence instantanée de la transformée en ondelettes sur un intervalle convenable. On peut extraire ainsi les lignes spectrales des composantes modulées en amplitude pour découvrir les lois de modulation. Pour l’analyse des sons FM, on peut extraire les points essentiels de la transformée en ondelettes qui décrivent le plan moyen de la trajectoire, nommé ridge. La restriction de la transformée au ridge donne un squelette de la transformée et avec lui on peut extraire le carrier, la modulation de la fréquence et la variation de l’index de modulation (Kronland-Martinet, 1991).
e) La re-synthèse et la transformation des signaux sonores.
On peut re-synthétiser un signal sonore à partir d’un son analysé par ondelettes en utilisant deux méthodes différentes: par synthèse granulaire et par synthèse additive généralisée. Ces deux méthodes nous permettent d’effectuer des modifications intimes des sons par l’altération des paramètres de la re-synthèse.
e.1) Re-synthèse granulaire.
Une formule de reconstruction du signal donné par Kronland-Martinet (1988) suggère une technique de synthèse granulaire qui consiste en une somme de tous les grains constitués par les ondelettes dilatées et déplacées avec un grain complexe équivalent aux coefficients obtenus par l’analyse. Une application digitale effectuée par lui associe une ondelette avec un poids approprié à chaque point de la grille d’analyse. Ces ondelettes chevauchées dans le temps peuvent être envisagées comme des "grains élémentaires". Ces grains auront toujours des formes un peu différentes à cause des modifications de phase occasionnées par la complexité des coefficients (Figure 12). La re-synthèse est effectuée par des modules constitués par quatre générateurs d’ondelettes (Figure 13). F. Boyer a développé ces unités et les a intégrées au programme Music V (Mathews, M. V. 1969). Dans cette application, un instrument complet est constitué par une série de modules, où chacun d’eux représente une voix différente de l’analyse (Il doit y avoir autant de modules que de voix existantes dans l’analyse).
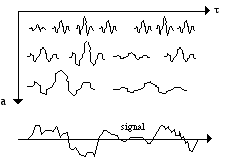
Figure 12.- Re-synthèse granulaire par somme sur une série d’ondelettes dilatées et tranlsatées avec des coefficients de valeur complexe dérivés de la transformée. (K-Martinet).
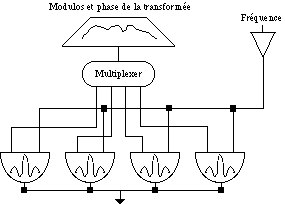
Figure 13.- Module pour la re-synthèse granulaire. La fréquence dépend des paramètres de dilatation associés avec la voix en considération. Un instrument complet requiert autant de modules que de voix dans l’analyse. (K-Martinet, 1991).
e.2) Synthèse additive généralisée.
D’autres formules de reconstruction du signal existent; Boyer et Kronland-Martinet (1989) en ont proposée une, qui implique seulement les valeurs de la transformée en ondelettes en un instant donné pour reconstruire la valeur correspondante du signal. Dans ce cas, pour chaque paramètre d’échelle de la grille d’analyse il est nécessaire d’utiliser les coefficients de tous les paramètres temporels de t (Boyer, Kronland-Martinet, 1989). Cette situation est très semblable à celle du Vocodeur de Phase où le problème se réduit à l’identification de la fréquence instantanée. La re-synthèse est nommée additive généralisé puisque les oscillateurs sont modulés autant en amplitude qu’en phase (Figure 14).
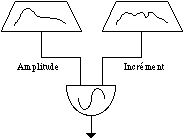
Figure 14.- Module de synthèse additive généralisé. L’instrument complet requiert autant de modules qu’il y a de voix dans la synthèse. (K-Martinet).
e.3) Transformation des sons.
Les techniques décrites nous permettent de transformer le signal sonore par la modification de trois différentes classes de paramètres: 1.- les coefficients obtenus par l’analyse; 2.- la géométrie de la grille utilisée pour la re-synthèse; 3.- dans le cas de la re-synthèse granulaire, l’ondelette utilisée pour la re-synthèse.
Filtrage du signal.
On peut par exemple extraire une note ou un accord donné d’un son si l’on force presque tous les coefficients à zéro (à l’exception de certains coefficients associés à certains paramètres d’échelle); on peut effectuer un filtrage highpass si l’on prend seulement les voix qui correspondent aux petites échelles, un filtrage bandpass si l’on prend seulement les voix des grandes échelles, ou simplement sélectionner différentes voix distribuées dans les différentes échelles de fréquence et éliminer les autres; on peut aussi construire un "equalisateur d’échelle" avec gains qui varient dans le temps sans problèmes de stabilité. Tous ces procédés sont encadrés dans la technique additive généralisée et ils sont de caractère linéaire.
Transposition temporelle.
Kronland-Martinet (1991) a effectué des transpositions temporelles différentes pour chaque voix dans l’analyse. Ce concept est très intéressant et ne paraît pas avoir été développé avec d’autres techniques d’analyse-synthèse. Ici les composantes spectrales de différentes voix se propagent à différentes vitesses. Le résultat est un signal sonore qui se propage en clusters, ce qui donne un effet sonore "aquatique". On peut bien sûr réaliser la transposition typique sans changement de durée effectué par d’autres techniques d’analyse-synthèse.
Transposition en fréquence sans modification de durée.
Boyer et Kronland-Martinet (1989) ont réalisé une addition des transpositions multiples (qui sont en rapport harmonique) pour chaque échelle du signal de manière synchrone. Ceci donne des effets de brillance (brightness ) très intéressants. Ce procédé est de caractère non-linéaire, car on effectue une modification indépendante pour le modulos et pour la phase des coefficients des ondelettes. Cette caractéristique de non-linearité fait aussi partie d’autres types de transformations telles que la transposition temporelle sans changement de fréquence et la synthèse croisée.
Synthèse-Croisée.
On peut effectuer une synthèse croisée si on prend le modulos des coefficients obtenus d’un son et les phases des coefficients extraits d’un autre son. L’interprétation des phases comme agent excitateur, et du modulos comme agent résonateur, nous amène naturellement à une "hybridation sonore" (Kronland-Martinet, 1991).
3.- Remarques.
L’analyse par ondelettes s’est révélé un outil remarquable pour l’analyse des signaux sonores à cause de sa double capacité de résolution dans les domaines du temps et de la fréquence. Sa caractéristique essentielle qui est d’être une technique temps-échelle, lui donne la capacité d’effectuer des analyses logarithmiques proches à notre perception auditive; de plus, sa capacité d’effectuer des analyses multirésolution progressives fait de cette analyse un instrument idéal pour la détection des motifs d’un signal et pour étudier des objets de type fractal. Des techniques d’analyse-synthèse comme la STFS ne sont pas capables d’analyser des sons complexes qui ont des discontinuités drastiques dans le temps; or, on sait que la plupart des sons dans la nature ont un comportement de ce type. Beaucoup de ces sons ont sûrement des structures de type fractal, et les ondelettes sont très appropriées pour pouvoir les étudier. Toutefois, la résolution de l’analyse par ondelettes en fréquence n’est pas optimale dans toutes les échelles, et on a parfois besoin d’avoir des informations précises sur les harmoniques aiguës d’un signal (les petites échelles en ondelettes ont une mauvaise résolution en fréquence). Pour cet effet, les techniques avec un filtre de largeur de bande constante sont plus appropriées que les ondelettes.
L’analyse par ondelettes a prouvé également qu’elle est un outil puissant pour la synthèse et la modification des signaux sonores. Il y a plusieurs types de coefficients dus à l’existence de diverses méthodes de transformation en ondelettes et de différentes classes de fonctions élémentaires (ou "grains"). Les différentes façons de manipuler ces coefficients donnent une grande diversité de transformations sonores. Ces coefficients ont parfois des caractéristiques qui permettent d’effectuer des opérations qu’on ne peut pas réaliser avec d’autres techniques, comme l’élimination de régions de bruit dans le signal par exemple. La re-synthèse par ondelettes a d’autres avantages comme l’utilisation d’un nombre de voix réduit.
Le grand problème de se servir des ondelettes pour la re-synthèse et la transformation des signaux sonores est la difficulté d’interpréter les coefficients. Pour cette raison, et peut-être aussi à cause des lourdes équations qui comportent les différentes transformées, on n’a presque pas développé des applications musicales. D’ailleurs, même celles qui ont été réalisées n’ont pas été à la portée des compositeurs de musique électroacoustique. Il est tout de même curieux que, vu qu’on a tellement parlé des ondelettes comme l’espoir des techniques d’analyse-synthèse, jusqu’à maintenant on n’a pas encore développé un outil avec une interface aimable pour les musiciens. Il faut espérer qu’on le fera bientôt, car ce sont les musiciens en collaboration avec les chercheurs qui font avancer le développement des outils musicaux de synthèse.
4.- Au delà des ondelettes.
"Alors qu’un unique algorithme (l’analyse de Fourier) convient à tous les signaux stationnaires, les signaux transitoires forment un univers si riche et si complexe qu’une seule méthode d’analyse ne peut en venir à bout" (Meyer, 1992).
Les ondelettes ne sont pas la panacée des techniques d’analyse-synthèse. On a déjà mentionné que pour analyser un signal stationnaire, il n’est pas raisonnable de l’analyser avec des petites ondelettes qui n’ont pas une bonne localisation en fréquence. La détermination imprécise des hautes fréquences constitue le principal défaut des ondelettes, particulièrement pour l’analyse de sons musicaux. Certains chercheurs ont reconsidéré l’analyse de Fourier d’un nouvel oeil et se sont inspirés du côté temporel des ondelettes pour essayer de créer des systèmes de représentation du signal offrant une bonne sélectivité en fréquence et une grande souplesse.
Un des premiers systèmes de représentation hybrides a été crée par Coifman et Meyer en 1989. Ils ont nommé leurs "grains élémentaires" paquets d’ondelettes. Un paquet d’ondelettes peut être défini comme le produit d’une ondelette par une fonction oscillante, où l’ondelette révèle les changements brusques pendant que l’oscillation révèle les variations régulières (Burke, 1995).
Avec les paquets d’ondelettes on fait varier indépendamment la taille de la "fenêtre", la fréquence et la position, tandis qu’avec les ondelettes, les "fenêtres" pour les fréquences aiguës sont toujours brèves, et les "fenêtres" pour les fréquences basses sont toujours longues. Le problème avec cette nouvelle technique, beaucoup plus complexe et subtil que l’analyse de Fourier à fenêtre, est que l’on ne sait pas encore bien interpréter les coefficients. Toutefois, ces paquets d’ondelettes ont déjà été utilisés pour étudier le phénomène de turbulence, pour comprimer des images, etc. Je pense que cette technique serait idéale pour l’analyse des sons avec des caractéristiques de transitoires d’attaque importantes et des régions spectrales stationnaires, qui ne sont pas bien localisées en temps et en fréquence par l’analyse de Fourier à fenêtre glissante (à cause de la fenêtre fixe) et par les ondelettes traditionnelles (à cause d’une mauvaise définition en fréquence pour les composantes aiguës). Il faudra attendre pour voir comment les chercheurs qui s’intéressent au domaine sonore utilisent cette technique.
Une autre famille hybride d’ondelettes a été créée par Coifman et Meyer. Les ondelettes de Malvar sont basées sur l’analyse de Fourier à fenêtre Gaussienne, mais puisque cette analyse ne peut pas être orthogonale, la forme de la fenêtre a été modifiée et les fonctions trigonométriques qui la remplissent, adaptées. La fonction de l’ondelette de Malvar commence par une attaque, elle forme ensuite un plateau et termine en decrescendo (Figure 15). La fonction est remplie soit de sinus, soit de cosinus, et elle a l’avantage d’avoir une signification physique beaucoup plus réelle que les ondelettes, car elle ressemble à une note d’un son instrumental naturel qui comporte une attaque, une période stationnaire et un amortissement (Meyer, 1992). On peut faire varier la taille de la fenêtre, et ces variations sont beaucoup plus souples que celles des ondelettes normales, car ici la taille de la fenêtre ne dépend pas du nombre d’oscillations comprises à l’intérieur. Avec une ondelette de Malvar, la durée de l’attaque de la période stationnaire et de l’amortissement peuvent varier de façon indépendante. Cette souplesse est très semblable aux fonctions d’onde formantique (ou FOF’s) (Rodet, 1979/84), où l’enveloppe des "grains" peut varier encore plus librement. Toutefois, les FOF’s ne sont pas des grains d’analyse.
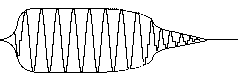
Figure 15.- Une ondelette de Malvar.
Avec les ondelettes de Malvar créées par Coifman et Meyer, on utilise un algorithme de segmentation automatique qui cherche à chaque fois le découpage le plus court. Malgré cette automatisation, ces ondelettes marchent assez bien pour analyser la parole. Des chercheurs comme Victor Wickerhauser les ont utilisées pour séparer de la parole les parties avec voix et les parties sans voix, et pour obtenir de petites segments ou unités similaires aux phonèmes (Burke, 1995). Selon Meyer, "la possibilité de découper un signal d’une façon non uniforme aidera les chercheurs qui analysent la musique ou la parole....car ceux-ci considèrent en priorité la dynamique du signal en fonction du temps avant de s’intéresser à son contenu fréquentiel global" (Meyer, 1992).
L’analyse par ondelettes de Malvar est prometteuse pour l’analyse des signaux musicaux, mais comme on l’avait déjà mentionné, en question de techniques d’analyse il n’y a pas d’absolu. La technique idéale n’existe pas, car le principe d’incertitude de Heisenberg va toujours agir sur les analyses faites. Les techniques hybrides s’adaptent peut-être mieux que les ondelettes normales à une analyse plus équilibrée des domaines temps-fréquence en musique, mais si on a un signal stationnaire, on s'adressera peut-être toujours à l’analyse de Fourier à court terme. Toutefois, on peut toujours mélanger toutes les techniques dans un même algorithme pour les rendre plus efficaces et anéantir un peu le principe d’incertitude. Coifman en a inventé une, nommée Best Basis. Cette géniale méthode choisit automatiquement le type d’analyse qui convient à un instant donné sur le signal. Si on a un trait périodique, l’algorithme choisit l’analyse de Fourier à court terme; si on a une segment irrégulier ou de type fractal, l’algorithme prend l’analyse par ondelettes, et si ni l’analyse de Fourier, ni celle des ondelettes ne convient pas tout à fait, alors Best Basis se sert de l’un de deux algorithmes hybrides qu’on vient de décrire. Je pense que cette philosophie d’hybridation pour l’analyse des signaux sonores (musicaux ou non musicaux) constitue l’avenir dans les techniques d’analyse-synthèse.
En question de synthèse, je crois que les "grains" des techniques hybrides peuvent être mieux adaptés que les ondelettes traditionnelles pour réaliser une re-synthèse granulaire (Boyer et Kronland-Martinet, 1989), parce que leur caractéristique est d’avoir des fonctions élémentaires plus semblables à des sons musicaux. Cependant, il faudra attendre pour savoir comment les chercheurs utilisent et développent ces techniques.
VI.- La synthèse granulaire fréquentielle synchrone.
On a parlé au deuxième chapitre de la classification que fait Roads des différentes techniques granulaires. La méthode de chevauchement des flots de fréquence-synchrone (pitch synchronous granular synthesis) peut être encadrée soit dans le groupe des techniques granulaires d’analyse synthèse (car elle effectue l’analyse des signaux), soit dans le groupe des techniques granulaires par formants, puisque la répétition synchrone des impulsions fréquentielles peut créer des effets d’amplitude modulée qui sont caractéristiques des sons formantiques. Toutefois, cette deuxième facette sera analysé dans le prochain chapitre.
1.- La méthode de Poli et Piccialli.
De Poli et Piccialli (1991) ont développé une méthode de synthèse granulaire pour des sons fréquentiels avec l’utilisation d’un modèle source-filtre. Leur méthode est bien adaptée à une série de techniques de synthèse (telles que la synthèse substractive et formantique) ainsi qu’à la compression temporelle des signaux sonores. Une des différences entre cette méthode et d’autres techniques d’analyse-synthèse étudiées dans ce chapitre est que chaque canal de la représentation d’une banque de filtres est décimé temporellement (c’est-à-dire, qu’il y a une compression du taux d’échantillonnage) pour pouvoir réduire la redondance du procès d’analyse. Pour la re-synthèse, les chenaux d’échantillons décimés (ou grains décimés) sont remis au taux d’échantillonnage d’origine et alimentés dans un filtre bandpass. Les opérations de décimation et d’interpolation des échantillons ne sont pas linéaires; elles produisent alisasing et imaging, et pour résoudre ce problème il faut reconstruire le signal avec des filtres de quadrature miroir (quadrature mirror filters ou QMF).
Pour effectuer la re-synthèse, chaque canal du modèle fonctionne comme un filtre de synthèse qui est excité par des impulsions équidistantes avec une amplitude et une phase convenables. La sortie (output) du synthétiseur donne comme résultat la convolution entre l’entrée (input) et la réponse impulsionelle du filtre. Dans le cas où l’on utilise des filtres de réponse finie (des filtres FIR), la sortie de chaque canal consiste en une séquence de "grains complexes" (De Poli et Piccialli, 1991). La méthode de De Poli et Piccialli peut avoir aussi une autre interprétation de la STFT; au lieu d’avoir une représentation d’une banque de filtres, on peut penser en termes d’une analyse de Fourier discrète par segments. Ces segments sont obtenus par la multiplication du signal par une fonction fenêtre. L’interprétation est la même que celle du Vocodeur de Phase (voir l’interprétation de Fourier du Vocodeur de Phase), où l’on chevauche les fenêtres d’analyse dans le temps, et ensuite on les additionne pour effectuer la re-synthèse du signal. Ce procédé est nommé aussi overlap and add (OLA).
L’interprétation du modèle source-filtre proposé par De Poli et Piccialli est constitué par des signaux quasi périodiques comme source d’excitation (un train de pulsations), et des filtres linéaires qui varient dans le temps comme l’enveloppe spectrale des pulsations. La fréquence des excitations quasi-périodiques est modifiée selon le ton du son désiré, et la largeur de bande du filtre (normalement un filtre avec phase linéaire qui varie dans le temps; un filtre FIR) change dans le temps, ce qui permet une modification du spectre du son. Toutefois, en réalité il n’y a pas des filtres. Les caractéristiques des filtres sont simulées par la forme d’onde des grains qui constituent le train de pulsations, et donc, la variation de la forme d’onde va déterminer l’enveloppe spectrale du son. Le but de cette technique de synthèse granulaire n’est pas de reconstruire le signal de manière exacte (même s’il est possible de le faire), mais plutôt de modifier les paramètres d’excitation et d’enveloppe spectrale pour synthétiser des sons nouveaux. Ces paramètres peuvent être estimés par une analyse linéaire prédictive (LPC) ou par une déconvolution homomorphique (De Poli et Piccialli, 1991).
Le modèle source-filtre est structuré par une banque des filtres FIR en parallèle qui sont excités par un train de pulsations, où chaque pulsation est en synchronie avec chaque période du signal. Cette structure permet d’avoir un bon contrôle des paramètres et rend le calcul efficient. Les pulsations, ou "grains", peuvent être localisés dans le cadre temps-fréquence, ce qui donne la possibilité d’utiliser chaque grain pour contrôler une zone particulière de fréquence dans le spectre. La grille de représentation granulaire dépend ici directement du son, tandis qu’avec la STFT et la transformée en ondelettes, les grains sont définis dans des grilles qui sont indépendantes du son (Figure 16). Cette caractéristique peut donner des avantages par rapport aux deux dernières techniques: 1.- dans la synthèse granulaire fréquentielle, la forme du grain varie dans les différentes couches des filtres ainsi que dans le temps, et on a comme conséquence un nombre de grains inférieur; 2.- l’aspect temporel est facilement séparé du côté spectral, tandis qu’avec les deux autres représentations, ces deux domaines sont fusionnés en magnitude et en phase; 3.- a cause des caractéristiques décrites auparavant, la synthèse granulaire fréquentielle bénéficie d’un contrôle naturel de la synthèse, et la modélisation de la forme d’onde du grain devient plus simple (De Poli et Piccialli, 1991).
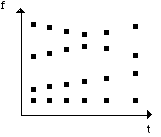
Figure 16.- Grille de Synthèse Fréquentielle Synchrone. Les grains sont synchronisés en correspondance avec le début de chaque période de la fréquence du son. Dans cet exemple la durée de la période augmente. (De Poli et Piccialli, 1991).
a) La forme d’onde des grains.
a.1) Structure directe du filtre.
Dans cette technique, l’enveloppe spectrale du son est déterminée par la transformation de Fourier du grain, tandis que les articulations fréquentielles du son sont déterminées par la localisation temporelle du grain. La forme d’onde du grain sera définie par des modélisations de filtres FIR standard. Toutefois, les filtres peuvent aussi être obtenus par une méthode fenêtre, où l’on multiplie la réponse impulsionelle par une fenêtre convenable. De Poli et Piccialli utilisent une fenêtre triangulaire, car leurs fonctions sont presque toujours continues et ont des dérivatifs continus (De Poli et Piccialli, 1991). On peut modéliser différents types de filtres, tels que des filtres linéaires en phase (qui sont essentiels quand on a plusieurs filtres en parallèle) ou des filtres avec phase minimale (qui servent pour la structure directe et sont plus économiques).
Le modèle créé par de Poli et Piccialli est amiable et transparent, car selon eux, l’utilisateur n’est pas forcé de connaître l’analyse de Fourier en profondeur, et il peut se servir des outils construits pour dessiner la fréquence spectrale désirée (au moyen d’un éditeur graphique).
a.2) Structure parallèle des filtres.
Dans la structure en parallèle, chaque séquence de grains contrôle une différente partie du spectre. On peut modéliser une forme d’onde spécifique à chaque instant, mais il faut créer quelques prototypes d’onde, et à partir de ceux-ci, effectuer des transformations pour obtenir les différents types d’onde dont on a besoin. On peut aussi utiliser des formes d’onde standard comme un exponentiel décroisant, une gaussienne, ou d’autres fenêtres qui fonctionnent comme enveloppes et qui sont utilisées dans l’analyse des signaux.
a.3) Transformations des formes d’onde.
Les équations utilisées pour la transformation des prototypes de formes d’onde sont assez complexes. Un musicien qui n’a pas une formation mathématique et de traitement du signal, pourra difficilement savoir comment effectuer ces transformations et quels sont leurs effets. Seulement avec un interface intelligent et aimable, on peut travailler avec cette technique, mais même ainsi, la correspondance entre forme d’onde et spectre n’est pas du tout évidente pour le utilisateur non spécialisé. Pour obtenir plus d’information sur les différentes transformations et ses équations il est conseillé de consulter directement la source: De Poli et Piccialli. 1991. "Pitch-synchronous granular synthesis". Dans G. de Poli, A. Piccialli & C. Roads, éditeurs, The representation of musical signals. MIT Press.
2.- Remarques.
La technique de De Poli et Piccialli est très proche des techniques granulaires formantiques, car sa conception est basée sur la séparation entre la source d’excitation qui donne la périodicité et la fréquence fondamentale du son, et le filtre ou enveloppe spectrale, que détermine les différentes fréquences du spectre. De ce fait, De Poli et Piccialli ont même développé une application de synthèse par formantes que l’on analysera dans le prochain chapitre.
Le problème d’avoir peu de renseignements sur l’interface développée pour l’application de cette méthode et l’insuffisance d’information sur les expériences sonores réalisées, fait qu’il soit difficile de critiquer cette technique. Cependant, si l’on fait une comparaison avec les techniques de synthèse formantiques qui utilisent des FOF, il me semble que celles-ci peuvent être plus puissantes, car elles bénéficient autant le domaine spectral que le domaine temporel du son. Avec la synthèse granulaire fréquentielle synchrone, on s’intéresse uniquement au côté spectral et par la création de sons plutôt stationnaires. Il est bien de pouvoir synthétiser des sons de ce type, mais on a des techniques granulaires formantiques qui peuvent le faire, et qui sont en même temps capables d’effectuer des transitions vers le domaine du discontinu (Eckel et Rocha Iturbide, 1995).
Il est intéressant de constater la grande ressemblance qui existe entre les grains de la synthèse fréquentielle synchrone et les FOF’s, des "grains" qui constituent des fonctions élémentaires avec un contenu spectral déterminé par leur enveloppe, leur largeur de bande et leur amplitude, et dont la fréquence fondamentale est déterminé par leur périodicité (voir chapitre suivant). Néanmoins, une grande différence est que la structure des FOF détermine directement le spectre du son, tandis que les grains dans la synthèse granulaire fréquentielle synchrone dépendent de la modélisation du filtre. Les particules sonores de cette dernière technique doivent être forcément de nature plus simple. On verra dans le chapitre suivant comment les FOF ont une enveloppe complexe constituée de trois différentes parties qui peuvent varier dans le temps avec une finesse incroyable. D’autre part, même si les FOF ont été utilisées principalement pour simuler des synthétiseurs à formants en parallèle, on a essayé aussi de les intégrer aux techniques d’analyse-synthèse (d’Alessandro, Rodet, 1989). Il y a encore des recherches à faire, mais ces grains pourraient être mieux adaptés pour effectuer la synthèse fréquentielle synchrone, et donner en même temps la possibilité d’effectuer des dé-synchronisations afin d’éliminer le statisme sonore.
VII.- Au delà de la granulation par analyse-synthèse.
1.- À la recherche de ponts entre la granulation par analyse-synthèse et les techniques traditionnelles de synthèse granulaire.
Les techniques de granulation par analyse-synthèse et les techniques de synthèse granulaire traditionnelles (QSGS, AGS, Granular Sampling), ont une même conception discrète de base: elles utilisent des particules élémentaires (ou "grains") pour la génération des signaux sonores. Toutefois, ces deux groupes de techniques ont différentes façons de construire ou de reconstruire le signal sonore, et chacun envisage une synthèse de sons très différente. La granulation par analyse-synthèse est centrée sur le contrôle fin des composantes spectrales (domaine de la fréquence), tandis que les techniques granulaires traditionnelles sont centrées sur le contrôle des particules élémentaires dans le temps (domaine du temps), et elles ne s’occupent pas d’avoir un contrôle précis du spectre. Le défaut du premier groupe de techniques est qu’il ne considère pas, ou qu’il n’a pas la faculté d’une plus grande flexibilité pour le contrôle des "particules élémentaires" dans le domaine temporel, et le défaut du deuxième groupe est d’être incapable de créer des sons en ayant un contrôle fin du domaine spectral.
Un des buts de ce travail est d’établir des ponts entre le domaine spectral et le domaine temporel dans la synthèse sonore au moyen des techniques granulaires, car leur caractère essentiel discret permet d’envisager la création de sons bien déployés, autant dans le domaine de la fréquence que dans le domaine du temps. Néanmoins, il faut utiliser certains techniques granulaires quand on veut travailler de manière précise sur le domaine des fréquences, et d’autres techniques quand on veut travailler sur l’aspect de la texture, de la masse, et du rythme. Or, y a-t-il des ponts possibles entre les différentes techniques granulaires, ou est-ce que l’on pourrait choisir une seule technique et l’utiliser pour travailler autant dans le micro-temps que dans le macro-temps et pour générer des sons spectraux, mais aussi des sons dont les composantes se déplacent plus librement dans l’espace au cours du temps?. Les techniques de synthèse granulaire traditionnelle qu’on a étudié dans le deuxième chapitre ne pourraient pas réaliser cette tâche, car elles ont une orientation non-analytique (Vaggione, 1993). Alors, est-ce que les techniques d’analyse-synthèse en seraient capables?.
Les recherches effectués dans le domaine de la granulation par analyse-synthèse ont été concentrées sur l’aspect du timbre dans le micro-temps, et les algorithmes crées pour effectuer des transformations sonores par la modification de l’analyse ont été presque toujours contraintes par les complications qui surviennent au moment de reconstruire le signal. Ces deux aspects, à mon avis, constituent les limitations principales de ce groupe de techniques. Le travail dans le macro-temps a été limité à des dilatations temporelles, ou au traitement de sons longs (où la quantité de mémoire RAM nécessaire devient prohibitive). Dans le cas de la dilatation, la transformation temporelle des sons ne produit pas de variations de timbre intéressantes. La synthèse de type spectral dans le macro-temps est plus efficace au moyen d’autres techniques non analytiques, telles que la synthèse additive. La variation des composantes spectrales dans cette dernière technique est très flexible grâce à des logiciels développés pour contrôler l’évolution précise de chaque partiel. Bien entendu, il s’agit ici d’une technique non analytique, et en ce sens, les techniques d’analyse-synthèse constituent un complément essentiel pour elle. Mais que faire si on veut obtenir des effets de caractère morphologique, ou qui se trouvent entre la continuité spectral des ondes et le domaine discontinu des grains?. Malheureusement, ni la synthèse additive, ni les techniques d’analyse-synthèse n’ont permis jusqu’à présent un travail sur les deux terrains.
Dans le deuxième chapitre, j’ai proposé d’utiliser la synthèse granulaire traditionnelle d’une manière semblable à la synthèse additive. Ceci permettrait d’avoir des sons spectraux qui peuvent évoluer vers des sons avec des caractéristiques de texture, et même vers une discontinuité totale qui devient rythme. Cependant, dans le champ spectral on a toujours des effets de modulation qu’on ne peut pas contrôler. Avec les techniques granulaires d’analyse-synthèse, on peut éviter ce type d’effets, mais on ne peut pas traiter les fenêtres d’analyse comme si elles étaient des grains qui peuvent se déplacer librement, car on perd le contrôle sur les phases, et on a comme conséquence des effets sonores indésirables. Néanmoins, l’idée d’avoir un contrôle aléatoire sur les fenêtres d’analyse a déjà existé, et a été appliqué dans certaines conditions où l’effet de bruit devient désirable. Xavier Serra et Julius Smith (1990) ont proposé une technique de synthèse par modélisation spectrale qui utilise une combinaison de décomposition déterministe et statistique. Ils utilisent la partie déterministe pour les composantes de type Fourier qui évoluent dans le temps, et la partie statistique pour recréer les éléments de bruit présents dans la portion d’attaque ou pendant la production d’un son (par exemple le bruit produit par un arc, par le souffle de la voix, etc) et qui ne peuvent pas être analysés de façon déterministe avec la transformée de Fourier (Vaggione, 1993). Avec ce procédé, on a confronté le dualisme acoustique (au niveau du micro-temps) entre le contrôle continu par analyse de grains, et le contrôle discontinu des grains, et on a obtenu de bons résultats. Alors, pourquoi ne pas développer cette idée et l’appliquer aussi dans le domaine du macro-temps?.
2.- Lecture discontinue de fenêtres.
Des transitions entre des sons spectraux et des ébranlements sonores (Xenakis, 1971) seraient possibles en utilisant des techniques d’analyse-synthèse. Il faudrait simplement avoir deux différents types de contrôle sur les fenêtres d’analyse ou "grains élémentaires": l’un qui corresponde aux algorithmes typiques avec lesquels on maîtrise les variations des fréquences dans le temps (sans désarroi des phases), et l’autre, complètement libre, avec lequel on peut faire évoluer chaque grain de façon totalement indépendante au moyen des algorithmes stochastiques, de chaos, etc.
Imaginons une analyse de Fourier à court terme avec une fenêtre de 1024 points. Si on a un taux d’échantillonnage de 44.1 Khz, notre taille de fenêtre est équivalente à un "grain" de 23.2 millièmes de seconde. Si on réalise une dilatation non linéaire, les valeurs de dilatation commencent à changer dans le temps, et on commence à écarter les fenêtres en ayant toujours un taux qui varie, mais de façon constant. Si on applique tout d’un coup un algorithme qui fait que les fenêtres s’écartent de façon discontinue et on commence aussi à changer la fréquence de chaque fenêtre, on aura des artefacts sonores, mais ensuite, les fenêtres deviendront des grains autonomes et on aura une synthèse granulaire asynchrone. En ce qui concerne la région où l’on a une désorganisation des phases, je pense que l’on doit pouvoir prévoir de manière statistique le type de bruit que l’on aura par rapport à l’algorithme que l’on veut utiliser.
Serra et Smith (Serra & Smith, 1990) ont utilisé un contrôle statistique sur les fenêtres d’analyse en utilisant toujours la même taille de fenêtre. Néanmoins, on pourrait aussi faire varier la taille au moment où l’on commence à séparer les fenêtres de façon discontinue; de cette manière on pourrait les agrandir en même temps qu’elles s’écartent et avoir alors des "grains" de plus en plus grands, et qui pourraient devenir des textures, et ensuite des motifs rythmiques. Les ondelettes de Malvar seraient peut-être idéales pour effectuer ce type de processus, car elles constituent des grains avec des caractéristiques musicales (leur attaque, corps et chute sont similaires aux notes des instruments), et en plus, leur taille change au cours du temps, de même que leur enveloppe.
Le processus que je viens de décrire n’est pas le seul possible. L’idée d’appliquer des algorithmes stochastiques aux "grains élémentaires" d’analyse peut être réalisé de différentes manières. Par exemple, avec les ondelettes, on a plusieurs échelles de "grains" de différente longueur (c’est-à-dire, différentes couches de "grains", chaque couche ayant des grains de longueur différente). On pourrait déconstruire un signal sonore de manière granulaire avant d’effectuer la re-synthèse, en éliminant de façon statistique des grains de différentes échelles. Cette granulation pourrait se faire de façon progressive entre les différentes échelles, et on pourrait ainsi avoir des effets de filtrage par zones spectrales; seulement, ici le filtrage est discret et discontinue, car on laisse toujours quelques grains dans les régions qu’on est en train de filtrer. Ce processus de type "passoire" fait partie d’une transformation dans le micro-temps, mais on pourrait aussi effectuer des dilatations et des contractions différentes pour chaque couche, en même temps que l’on effectue la déconstruction granulaire, ou au contraire, on pourrait combiner l’effet "aquatique" de changement temporel (effectué par Kronland-Martinet) avec une surproduction d’ondelettes contrôlées de manière stochastique, en utilisant différents algorithmes et différentes densités sur chaque couche de grains.
On peut imaginer d’autres types de contrôle de "grains élémentaires" d’analyse. Par exemple, l’idée d’avoir différentes techniques d’analyse combinées dans un même algorithme (Best Basis ), qui a été proposée par Coifman (1992), pourrait être utilisée en musique pour l’analyse, la transformation, et la re-synthèse. Ainsi, on aurait une gamme de grains assez différents au moment de reconstruire le signal. Il y a enfin une grande variété de possibilités pour le mélange des transformations courantes des techniques d’analyse-synthèse et des transformations des techniques granulaires traditionnelles. Mais est-ce que cette mixture pourrait vraiment nous conduire à la création d’une synthèse globale, avec laquelle nous serions capables de travailler dans les différentes échelles du temps simultanément?.
3.- À la recherche des techniques d’analyse-synthèse qui fonctionnent dans les différentes échelles temporelles.
On a étudié les problèmes qu’on a rencontré avec l’analyse d’un signal sonore, particulièrement ceux qui concernent le principe d’incertitude de Heisenberg. D’autre part, on sait que l’analyse globale d’un signal déployé autant dans le micro-temps que dans le macro-temps sera toujours difficile, car l’interaction entre les différentes échelles temporelles est de caractère non-linéaire, et on doit en plus tenir compte du contexte musical (Vaggione, 1993). Toutefois, on a vu aussi qu’une série de techniques nouvelles (ondelettes) et leur hybridation peuvent être d’une aide précieuse pour améliorer la situation. Le principe d’incertitude sera toujours là, mais des "grains élémentaires" tels que les ondelettes qui fonctionnent dans différentes échelles temporelles (et qui sont précises en temps), en combinaison avec des grains plus précis dans le domaine de la fréquence, peuvent être combinés pour obtenir une analyse plus précise et globale.
En ce qui concerne la transformation et la re-synthèse d’un signal sonore, on a les mêmes problèmes que pour l’analyse, mais notre attitude est beaucoup plus détendue et flexible, car ce qui nous intéresse est la création de sons nouveaux tout en gardant un contrôle complet au moment de les réaliser, en ayant toutefois une certain marge d’erreur qui peut être prévisible avec un peu d’expérience. L’interaction non-linéaire entre les différentes échelles rend difficile la tâche d’effectuer une synthèse globale dans le micro et le macro-temps. Selon Vaggione, on ne peut pas avoir une syntaxe commune pour travailler dans les différents domaines du temps (Vaggione, 1993). Il est vrai que si l’on veut unir les techniques d’analyse-synthèse (qui fonctionnent mieux dans le micro-temps), aux techniques de synthèse granulaire traditionnelles (qui fonctionnent mieux dans le macro-temps) il faut recourir à une série d’algorithmes de contrôle différents qui ont des conceptions de syntaxe différentes. Ceci rend possible la création d’une technique de synthèse qui englobe les domaines temps-fréquence de façon équilibrée. Toutefois, on aura toujours des effets non contrôlables, mais que l’on peut plus ou moins prévoir et utiliser en notre faveur. Peut-être que ces moments d’indétermination inévitables - où l’on n’est ni dans le domaine du contrôle fin des fréquences, ni dans le domaine du contrôle stochastique des textures, des masses, et du rythme - pourraient être observés, acceptés, et mis en valeur musicale avec une philosophie cageienne.
Deux dernières remarques: il n’est obligé que le contrôle des "grains" dans le macro-temps soit de caractère stochastique; on peut avoir des structures granulaires prototypes préconçues et qui sont déclenchées par des algorithmes de base qui peuvent à leur tour être transformés. On développera ce sujet dans le chapitre six sur les différents mécanismes de contrôle des grains. D’autre part, mes propositions dans cette dernière section du chapitre demeureront théoriques (et peut-être utopiques?) car malheureusement, je ne suis ni mathématicien, ni spécialiste en traitement de signal, et par conséquent, je n’ai aucun moyen de les mettre en forme. J’espère tout de même qu’elles auront quelque utilité, et qu’un chercheur s’y intéressera et en tiendra compte d’elles pour réaliser des expériences. Néanmoins, l’idée d’incorporer le micro-temps avec le macro-temps dans une même technique de synthèse a été développée de façon théorique et pratique par moi et par Gerhard Eckel au moyen de la synthèse granulaire formantique (Eckel, Rocha Iturbide, 1995). Cette technique (qui n’appartient pas aux techniques d’analyse-synthèse) fonctionne bien dans les domaines du temps et de la fréquence, et elle pourrait être incorporée aux techniques d’analyse-synthèse (Rodet et d’Alessandro, 1989) et servir de "lapis philosophale" pour la création d’une synthèse multi-échelles. Cette méthode sera traitée en détail dans le chapitre suivant.