FOOTNOTES ON THIS CHAPTER ARE NOT YET IMPLEMENTED!
CHAPITRE V: LA SYNTHÈSE GRANULAIRE EN COMBINAISON
AVEC D’AUTRES TECHNIQUES DE SYNTHÈSE.
Dans le deuxième chapitre, j’ai traité les différentes caractéristiques des particules élémentaires dans la synthèse granulaire. Du point de vue du timbre, la caractéristique des grains la plus importante est peut-être leur forme d’onde. Quand on utilise des grains synthétiques, les diverses façons de générer la forme d’onde de chaque grain sont liées aux différentes techniques de synthèse qu’on connaît. Donc, on a une gamme très variée de possibilités pour générer des grains avec un timbre différent. J’ai déjà parlé des diverses applications qui ont utilisé des grains générés par fréquence modulée (FM) (Truax, 1986. Jones et Parks, 1987), ainsi que des applications qui ont utilisé des grains générés par synthèse additive (Truax, 1988. Roads, 1991). D’autre part, on a vu aussi qu’on peut générer les grains à partir des échantillons. Cette technique s’appelle granulation temporelle, et avec elle on peut effectuer certains traitements du signal semblables à ceux des techniques d’analyse-synthèse, comme la dilatation et la contraction temporelle, et la synthèse croisée (voir deuxième chapitre).
Dans ce chapitre j’analyserai d’autres possibilités de génération de la forme d’onde des grains, mais surtout, on verra comment on peut mélanger le résultat global de la synthèse granulaire avec d’autres techniques de synthèse, c’est-à-dire, la réalisation de la synthèse granulaire quel que soit le type d’onde des grains, et ensuite le traitement du son résultant, soit en utilisant les techniques d’analyse-synthèse, les techniques de synthèse substractive, les techniques de traitement d’enregistrements (Smith, J.O. 1993), ou autres techniques.
I.- La synthèse granulaire et la convolution.
1.- La convolution.
Quand deux formes d’onde sont multipliées, le spectre de la forme d’onde résultante n’est pas le produit des deux spectres des formes d’onde prises individuellement. Le spectre de deux formes d’onde est la convolution des spectres de deux formes d’onde individuelles (Moore, 1990). La convolution constitue la multiplication de deux spectres, et peut être représentée par l’équation suivante: DFT(f (n) g (n)) = F (k) * G (k)
où f (n) et g (n) constituent le nombre d’échantillons des deux formes d’onde; F (k) et G (k) constituent les spectres de deux formes d’onde (les spectres sont calculés par la transformée discrète de fourier); et où * indique la convolution entre les deux spectres. Dans cette convolution, chaque point dans le spectre discret de fréquence de l’entrée F est convolué avec chaque point du spectre discret de l’entrée G .
Le résultat de la convolution entre deux signaux sonores est une espèce de synthèse croisée où les fréquences communes des deux spectres sont renforcées (Erbe, 1992, 1994). Ce résultat équivaut au filtrage du spectre d’un son par le spectre d’un autre son (Roads, 1993a). Toutefois, l’effet de la convolution peut être relié à d’autres types de transformations sonores comme la spatialisation, la modulation, les modèles d’interaction entre sources d’excitation/résonance, et des transformations temporelles telles que: lissement d’attaques, échos multiples, simulation d’une pièce, barbouillement dans le temps, et réverbération.
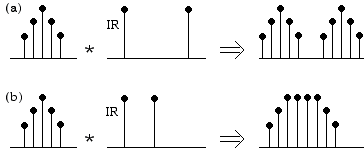
Prenons les transformations temporelles et donnons un exemple. La création d’échos multiples se fait en multipliant des impulsions courtes qui sont espacées par des silences suffisamment longs, avec un signal sonore déterminé. Ici, le résultat de la convolution est égal à la répétition dans le temps du signal sonore à l’entrée, car toutes les amplitudes des fréquences du signal sont multipliées par une constante (toutes les fréquences du spectre des impulsions ont la même amplitude) (Figure 1a). Dans cette conception temporelle de la convolution, les sons granulaires peuvent jouer un rôle intéressant. Par exemple, pour effectuer la réverbération d’un son au moyen de la convolution, on utilise un bruit blanc avec une enveloppe d’amplitude exponentielle décroissante. Des réverbérations colorées peuvent être obtenues si on utilise des nuages granulaires avec une bande de fréquence large et de haute densité, et avec une amplitude exponentielle décroissante. On parlera en détail de ces effets un peu plus tard.

Figure 1.- a) La convolution d’un signal a avec un signal b qui contient deux réponses impulsionnelles suffisamment espacées donne comme résultat la répétition de l’écho de a à l’endroit de la deuxième impulsion de b . b) Quand les impulsions de b se rapprochent, les partiels de a commencent à se chevaucher (Roads, 1993a).
Pour conclure cette section, il ne faut pas oublier que l’effet de la convolution dépend entièrement de la nature de deux signaux sonores à l’entrée. La convolution pure ne bénéficie pas d’un contrôle des paramètres. Par exemple, l’équilibre de la mixture entre deux spectres convolués ne peut pas être altéré; il sera toujours le même. Donc, pour bien profiter de la convolution, il faudra bien connaître les différents résultats des diverses combinaisons des signaux sonores, ainsi que la cause de ces résultats; de cette manière, avec un peu de pratique on réussira à les prévoir.
2.- Les différentes transformations sonores au moyen de la convolution.
Je vais décrire les différentes transformations sonores effectuées avec la convolution selon la classification et les expériences réalisées par Curtis Roads (Roads, 1993a), et je vais élargir cette liste en ajoutant mes propres expériences et conclusions.
a) Filtrage-croisé.
Les effets du filtrage d’un son par un autre sont les suivants:
· Si les deux signaux sont longs en durée et l’un des deux signaux à l’entrée a une attaque lisse, l’effet dominant de la convolution est une altération spectrale.
· Si les deux sources ont une durée longue et chacune a un ton fort, et si l’une des deux sources a une attaque lisse, le résultat contiendra les deux tons et l’intersection de leur spectre. Ceci constitue une espèce de mixage, mais où les résonances communes des deux tons sont renforcées.
· La convolution est particulièrement sensible aux caractéristiques de l’attaque des sources. Si l’une de deux sources a une attaque lisse, le résultat de la convolution aura toujours une attaque lisse.
· On ne peut pas altérer l’équilibre entre les deux spectres.
a.1) Auto-filtrage.
Ceci constitue un effet que j’ai découvert et que j’ai beaucoup utilisé pour dévoiler ou renforcer les fréquences spectrales prédominantes d’un son. Cette technique fonctionne particulièrement bien quand on a un son avec des bandes spectrales bruiteuses que l’on veut faire disparaître. Par exemple, dans l’enregistrement du crissement des pneus d’une voiture, le bruit du moteur est inévitablement inclus. Puisque seul le crissement m’intéressait (un ton clair avec quelques composantes spectrales en fréquence), j’ai convolué l’enregistrement du son de la voiture avec lui même. Le résultat a été un anéantissement en dB du bruit du moteur et une intensification des fréquences prédominantes du crissement des pneus. Avec de sons encore plus bruiteux dont on a seulement quelques composantes spectrales en fréquence isolées et claires, on peut tout de même les faire ressortir en convoluant le son avec lui-même, puis en convoluant le résultat avec lui-même, et ainsi de suite.
b) Échos.
Les effets d’écho s’expliquent de la façon suivante: toutes les réponses impulsionelles (IR) dans une des entrées de la convolution ont comme résultat la copie de l’autre signal.
· Pour créer un effet d’écho multiple, il faut simplement convoluer un son avec une série d’impulsions séparés par les temps de delai désirés (Figure 2).
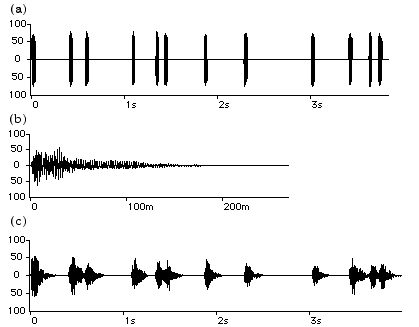
Figure 2.- Convolution d’un motif rythmique d’impulsions (ou grains) avec un son de pizzicato de violon. (a) Impulsions. (b) Pizzicato. (c) Convolution.
c) Simulation d’une pièce.
· Pour simuler l’effet d’un son qui se joue dans une pièce (ou une salle) quelconque, il faut simplement enregistrer la réponse impulsionelle (IR) de la pièce (sa réponse à une impulsion forte, comme un frappement de mains par exemple). Si cette IR est convoluée avec un son arbitraire, il paraîtra que le son a été joué dans cette pièce.
d) Positionnement spatial.
Cette technique est semblable à la précédente, mais elle a besoin d’avoir les sons convolués enregistrés dans un format à chenaux multiples.
· Pour positionner un son dans un point précis dans l’espace il faut générer une impulsion sur ce point et convoluer le son avec un enregistrement à chenaux multiples de la réponse impulsionelle de cet espace.
e) Réverbération.
· Pour générer une réverbération élémentaire il faut convoluer un signal avec du bruit blanc, où le bruit a une attaque pointue et une chute exponentielle. La durée du bruit détermine le temps de réverbération.
· Pour colorer cette réverbération il faut filtrer le bruit avant de le convoluer.
· Si le bruit a une chute logarithmique (et non exponentielle), le son à l’entrée apparaît suspendu dans le temps avant la chute.
On peut aussi utiliser un bruit granulaire de haute densité avec un décroissement exponentiel pour générer une réverbération colorée.
f) Modélisation d’excitation/résonance.
Beaucoup de sons instrumentaux ou vocaux peuvent être simulés par un modèle séparé en deux parties: un signal d’excitation qui est filtré par un signal de résonance. L’excitation constitue l’action de la vibration d’une corde, la vibration d’une anche, ou un flux d’air dans un tube. La résonance est la réponse du filtrage du corps d’un instrument. La convolution nous permet d’explorer un monde virtuel où un son excite les résonances d’un autre son (Roads, 1993a). Ces deux sons peuvent être très différents, et l’on peut effectuer ainsi des croisements très divers. Par exemple, on peut faire résonner un gong avec des attaques de pizzicato d’un violoncelle.
· Pour bien réussir une simulation, l’excitation doit être brève, un signal de type impulsionel (percussif), avec une ou plusieurs attaques pointues. La résonance peut constituer n’importe quel son.
Dans le chapitre précédent, on a analysé la technique granulaire formantique de De Poli et Piccialli (1991) qui utilise la conception d’excitation/résonance, en effectuant une convolution entre un train d’impulsions (les grains) et diverses formes d’onde qui donnent les qualités spectrales du son résultant. En fait, la convolution peut constituer une technique de filtrage formantique assez précise quand on l’envisage dans une technique d’analyse-synthèse comme celle-ci. D’autre part, la synthèse croisée avec les méthodes d’analyse-synthèse s’effectue aussi par une convolution, soit par la séparation de la source et la résonance (Arfib, 1991), soit simplement en multipliant les deux signaux sonores (Dolson, 1984). La première de ces techniques possède un contrôle majeur du spectre car on sépare chaque grain d’analyse en deux grains différents (grain-source et grain-réponse) au moyen d’une opération de type discret qui nous permet d’affecter chaque paire de grains de l’analyse et d’avoir ainsi des transformations qui changent de manière plus fine dans le temps.
3.- La convolution avec des sons granulaires.
"The rolling of thunder has been attributed to echoes among the clouds; and if it is to be considered that a cloud is a collection of particles of water....and therefore each capable of reflecting a sound, there is no reason why very [loud] sounds should not be reverberated....from a cloud".
Sir John Herschel, dans Tyndall (1875).
Les nuages peuvent agir comme des réverbérateurs atmosphériques. Certains scientifiques du dix-neuvième siècle avaient observé que dans un ciel limpide, des tirs de canon étaient pointus, alors que quand le ciel était couvert de nuages, les tirs étaient accompagnés par un roulement ondulatoire semblable au tonnerre (Roads, 1993a). La convolution d’une impulsion avec un nuage granulaire peut créer un effet analogue à celui de la réverbération atmosphérique. Roads appelle cet effet time-splattered (éparpillement ou aspersion dans le temps) pour traduire la non-uniformité des particules sonores dans cette réverbération granulaire. Avec la convolution entre un nuage granulaire AGS de large densité conformé par des particules sonores avec une réponse impulsionelle bien pointue, et un signal sonore, on pourrait imaginer comme résultat des centaines d’échos. Toutefois, la proximité des grains crée des effets de barbouillement et de time-splatter qui vont dépendre des caractéristiques de l’attaque du signal sonore à l’entrée. Voici les deux principaux effets:
· Si le signal sonore à l’entrée commence avec une attaque pointue, chaque grain génère un écho de cette attaque. Si le nuage de grains n’est pas continue, alors les échos sont espacés de manière irrégulière dans le temps.
· Si le signal sonore à l’entrée a une attaque lisse, le time-splattering est lissé et devient une étrange réverbération colorée (Roads, 1993a). La couleur de la réverbération est déterminée par le spectre des grains - un facteur de leur durée, enveloppe, et forme d’onde.
Les effets de la convolution avec des grains sonores peuvent beaucoup varier selon les propriétés du nuage granulaire et le signal à l’entrée. Si les grains sont courts, espacés, pointus en attaque, et bruiteux en contenu spectral, et s’ils sont convolués avec un son aussi pointu en attaque, on aura comme résultat des échos clairs du son à l’entrée et peu d’effets de time-splattering. Voici une série d’effets possibles décrits par Roads (1993a):
· Pour une attaque pointue à l’entrée, une convolution avec une douzaine de grains courts en durée crée une distribution statistique d’échos du son à l’entrée (Figure 2).
· Le grains longs accentuent l’effet de barbouillage dans le temps (time-smearing).
· Quand le son à l’entrée a une attaque lisse, le résultat est un filtrage qui varie dans le temps et qui dépend du spectre des grains.
· Plus dense sera le nuage, plus les échos seront fusionnés dans un effet de réverbération.
J’ajouterai un effet très intéressant produit par un nuage de grains d’une durée de 20 à 40 millièmes de seconde avec une enveloppe gaussienne (ou d’un autre type), et un contenu spectral harmonique ou inharmonique (mais non bruiteux), convolué avec le ton d’un instrument d’attaque pointue (un pizzicato, une attaque de piano ou de clavecin, une attaque de xylophone, etc). Le résultat n’est pas la simple répétition des échos du son d’origine, mais la variation spectrale de ce son à chaque nouvel écho. Ceci est dû à l’interaction entre la variation du spectre et de la fréquence des grains, et le spectre du ton instrumental. Avec un nuage de grains qui varient en fréquence mais avec un contenu spectral bruiteux, l’effet résultant du spectre final sera toujours plus ou moins pareil, sauf si la densité et les fréquences des grains du nuage varient radicalement, mais même ainsi les changements du spectre des échos ne seront pas aussi nets qu’avec un nuage de grains non bruiteux. D’autre part, si on réalise cette même expérience avec un son harmonique à l’entrée, comme un accord chanté par un choeur, le résultat sera l’accentuation des différentes notes de l’accord selon la fréquence et le spectre des grains convolués avec lui (voir exemples sonores dans l’appendice).
J’ai effectué plusieurs expériences de convolution des sons granulaires synthétiques AGS avec des signaux sonores des tons et des bruits d’instruments à vent cuivrés. Si l’attaque du ton instrumental était pointue, alors les échos étaient plus nets, mais tout de même time-smeared et time-splattered, tandis qu’avec un son de soufflement dans le trombone, le résultat a été une réverbération colorée du bruit du soufflement, mais avec la résonance du corps du trombone (produit par le soufflement) beaucoup plus renforcée (voir exemples sonores dans l’appendice). Dans le cas des échos, il est possible que les effets de time-smearing et de time-splattering aient été créés par l’insuffisance d’une attaque pointue des grains synthétiques, car j’ai utilisé l’enveloppe gaussienne standard utilisée par Gabor et Roads (Roads, 1993b). Pour avoir des échos nets il faut avoir des enveloppes rectangulaires, trapézoïdes, ou triangulaires. L’enveloppe rectangulaire est peut-être la plus efficace, avec l’avantage que dans le cas de la convolution on n’est pas gêné par la création des effets de modulation (Roads, 1991); au contraire, plus bruiteuse sera l’enveloppe, on obtiendra des échos plus nets. Pour parvenir plus facilement à ce résultat, il serait également souhaitable d’avoir des formes d’onde plutôt bruiteuses et des grains assez courts. Toutefois, on pourrait aussi rechercher le mixage du contenu spectral des grains avec le spectre du signal sonore, ainsi que diverses variations de l’effet de time-smearing et de time-splattering; pour ceci, on pourrait réaliser un nuage de grains synthétiques dont la durée, le contenu spectral, les enveloppes et l’espacement pourraient varier dans le temps, et l’on pourrait effectuer ainsi un continuum entre les différents effets d’écho et de réverbération (Figure 3).
La convolution entre deux sons granulaires est également possible, mais le résultat n’est pas très prévisible et des effets de barbouillage, de time-smearing et de time-splattering vont prédominer. Toutefois, le contour des bandes de fréquence des nuages sont toujours reconnaissables. En revanche, les effets à l’intérieur des bandes seront parfois semblables à des effets sonores aquatiques, avec des portions plus ou moins réverbérées, et avec d’autres portions plus ou moins bruiteuses (Figure 4).
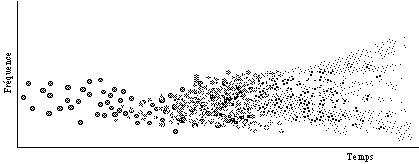
Figure 3.- Avec une planification soigneuse du contenu spectral des grains et de leur espacement, on peut réaliser une convolution avec un signal sonore et obtenir un continuum entre différentes effets d’écho et de réverbération.
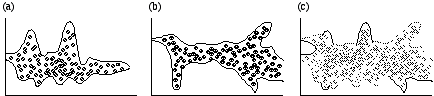
Figure 4.- La convolution du nuage granulaire (a) avec le nuage granulaire (b) donne le nuage granulaire (c). Ce résultat est un mélange d’effets de réverbération aquatiques, de barbouillage, et des bandes bruiteuses. Les seules éléments de (a) et (b) qui peuvent être reconnaissables dans (c) sont les contours des largeurs de bande des nuages granulaires.
On n’est pas obligé d’utiliser des sons granulaires synthétiques ou même des granulations d’échantillons (où les effets seraient particulièrement intéressants) pour effectuer la convolution avec un signal sonore. On peut aussi utiliser des sons de type granulaire issus de la nature tels que la pluie, les craquements du feu, des sons de feux d’artifice, des sons de grains jetés par certaines plantes au printemps, etc. L’avantage avec ces sons est qu’on a des rythmes stochastiques très intéressants dès le départ, qui pourraient être utilisés pour produire des séquences sonores dans la composition électroacoustique dans le domaine de la macro-forme. J’ai moi même créé des sons en utilisant le bruit de la pluie sur le plafond en bois de mon ancien appartement à Paris, convolué avec des cloches et avec d’autres sons instrumentaux, et j’ai obtenu des résultats très intéressants (voir exemples sonores dans l’appendice).
Pour conclure cette section, il faut se rappeler qu’il y a des techniques granulaires synchrones (De Poli et Piccialli, 1991) et d’analyse-synthèse (Dolson, 1984. Arfib, 1991) qui utilisent la convolution comme une partie intrinsèque de leur fonctionnement. Dans certains de ces techniques, on bénéficie d’un contrôle spectral plus fin grâce à l’analyse et à la séparation des grains d’analyse en deux grains différents, l’un agissant comme impulsion et l’autre comme filtre.
II.- La synthèse granulaire et les filtres.
On peut considérer que la convolution est dans un certain sens une technique de filtrage, mais où l’on a un contrôle de paramètres assez restreint (sauf avec certaines méthodes d’analyse-synthèse); pourtant, la convolution est également utile pour créer des transformations sonores dans d’autres domaines de la synthèse (comme on vient de le voir). En revanche, avec les techniques de filtrage traditionnelles on possède un contrôle total et l’on peut sculpter le son avec une grande précision. Le filtrage agit sur un signal sonore soit par la décroissance d’amplitude de certaines composantes spectrales (synthèse substractive), soit par l’augmentation d’amplitude de certaines composantes spectrales. Dans le deux cas, on a besoin d’avoir un signal à l’entrée des filtres avec un spectre large et riche, comme du bruit blanc ou des impulsions étroites (narrow pulses). Pour cette raison, des nuages granulaires pourraient très bien servir comme matière première. D’autre part, on peut créer des résonances de type formantique en utilisant des filtres de deuxième ordre avec une largeur de bande étroite, qui vont dépendre de la fréquence et de la largeur de bande du filtre, mais aussi de l’énergie spectrale de la source; finalement, on peut aussi créer des effets de réverbération en utilisant des filtres réverbérateurs tels que les filtres en peigne (comb filters), qui fonctionnent au moyen de lignes de délai bouclées et qui font sonner leur fréquence fondamentale en même temps que les fréquences déterminées du spectre du signal à l’entrée.
Toute cette gamme d’effets que je viens de décrire peut être appliquée à la synthèse granulaire. Il y a deux façons différentes de le faire. La première est la plus simple: on crée un son granulaire ou un nuage granulaire et on travaille ensuite sur ce résultat avec un programme d’analyse-synthèse, de synthèse substractive, etc. La deuxième est plus compliquée mais plus intéressante. On peut réaliser une application de synthèse granulaire où le filtrage des grains se fasse en même temps que la synthèse. Ceci peut d’ailleurs être effectué de deux manières différentes: l’une par le filtrage des grains à niveau individuel, et l’autre par le filtrage du résultat global. Dans le logiciel GiST (Eckel, Rocha Iturbide, 1995) on réalise le filtrage des particules sonores au niveau individuel à cause des caractéristiques formantiques des grains nommés FOF (Fonctions d’onde formantiques) qui possèdent un paramètre qui modifie leur largeur de bande. Ceci est un facteur très avantageux car on peut effectuer des sons granulaires où l’on peut générer des régions plus résonantes ou plus bruiteuses au niveau du quantum sonore (voir quatrième chapitre).
1.- Filtres substractifs.
Le filtrage substractif est la plus commune des techniques de filtrage. On peut effectuer cette technique soit au niveau du grain, soit au niveau global. Toutefois, je crois qu’il est plus logique de l’utiliser en partant du résultat globale du nuage granulaire, car celui-ci constitue la matière première essentielle à être sculptée. Je peut facilement imaginer un nuage granulaire avec une bande de fréquence assez large qui varie dans le temps, et ensuite la sélection de différentes régions du nuage pour être anéantis ou renforcés en amplitude. De cette manière, on peut faire ressortir de nouveaux nuages en partant de la première, chacune une avec un niveau d’intensité différent (Figure 5). La manière la plus simple d’effectuer ce procédé serait d’utiliser une technique d’analyse-synthèse tel qu’Audio-Sculpt (IRCAM) au moyen des filtres passe-bande qui varient dans le temps.

Figure 5.- Filtrage de trois bandes de fréquence d’un nuage granulaire. La bande la plus aiguë augmente l’amplitude des grains tandis que les deux autres bandes éliminent complètement l’amplitude des grains. Le résultat est la génération de trois nouveaux nouages granulaires extraits du premier nuage. Les grains du nuage du dessus possèdent une amplitude majeure.
2.- Filtres résonateurs.
Les filtres résonateurs typiques utilisés dans les systèmes informatiques musicaux sont communément appelés RESON (Dodge, Jerse, 1985). Ces filtres de deuxième degré créent des régions formantiques résonantes en partant des sons avec une bande spectrale large et homogène tels que du bruit blanc. Néanmoins, on peut aussi utiliser des sons bruiteux avec des bandes de fréquence larges qui ont de l’énergie spectrale distribuée de manière homogène. Les nuages granulaires s’adaptent très bien à ce type de filtrage.
Le logiciel Csound (Vercoe, 1986) possède des filtres très efficaces pour créer des régions formantiques résonantes. On peut par exemple effectuer un filtrage avec une série de filtres en parallèle (chacun avec une fréquence différente et qui peut évoluer dans le temps) en partant d’un son granulaire qu’il faudrait synthétiser au préalable. La différence entre l’utilisation d’un son granulaire comme matière première au lieu de bruit blanc, est une légère variation de l’intensité et de la couleur des sons fréquentielles résultantes. Cependant, quand les grains du nuage ont une attaque pointue et la densité du nuage n’est pas très haute, on peut avoir aussi des résonances semblables aux sons de cloches ou de clochettes (selon la fréquence des filtres). Le contenu spectral de la matière première sonore utilisée disparaîtra toujours complètement, et les paramètres formantiques des filtres seront perceptibles seulement dans le résultat final. La seule variation importante au moment d’utiliser divers sons granulaires est la qualité de la résonance des filtres du point de vue morphologique; pourtant, le contenu spectral sera toujours plus ou moins pareil.
Avec l’application de la synthèse granulaire à partir d’échantillons que j’ai développée à l’IRCAM en 1993 avec Csound et PatchWork (Rocha Iturbide, 1994), il serait possible de réaliser une application de filtrage au niveau du grain si on utilise des sources sonores avec un spectre dense. La variation de la largeur de bande des filtres pourrait alors faire ressortir plus ou moins l’échantillon d’origine, et on pourrait effectuer des processus entre des résonances granulaires pures et les grains d’origine. D’ailleurs, ce procédé ressemble un peu au procédé effectué avec des grains FOF du logiciel GiST (Eckel et Rocha Iturbide, 1995), sauf qu’avec cette dernière technique, lorsqu’on a une largeur de bande égale à 0 Hz (résonance maximale) la résonance du filtre n’est pas très nette (comme avec les filtres RESON de Csound); on conserve les caractéristiques spectrales des grains de l’échantillon lu, avec un tout petit peu de résonance (voir logiciel GiST dans le quatrième chapitre). Cependant, en augmentant la largeur de bande, on aura un effet chaque fois plus bruiteux, semblable à celui du filtre RESON de Csound (quand on augmente sa largeur de bande).
3.- Filtres formantiques.
On peut appliquer un filtrage par régions formantiques à un nuage granulaire, et simuler ainsi une voix ou d’autres instruments à caractère formantique qui vont se déplacer dans le nuage. Dans la technique d’analyse-synthèse SVP (Depalle, P., Poirot, G. 1991), le filtrage formantique constitue une des différentes possibilités des techniques de filtrage. On peut choisir plusieurs séries de régions formantiques en parallèle, et les interpoler ensuite de façon linéaire; de cette manière, on peut par exemple effectuer des transitions continues entre des sons formantiques de la parole (de la voyelle a à la voyelle i, ensuite à la voyelle o , etc). Le bruit blanc est typiquement utilisé comme matière première pour le filtrage, mais on peut aussi utiliser des nuages granulaires qui vont modifier la couleur de la résonance des régions formantiques. Ces filtres sont différents des filtres utilisés dans la fonction RESON de Csound, car ils n’éliminent pas le reste du signal sonore; donc, on peut par exemple filtrer un gong avec les régions formantiques des voyelles aiou et percevoir en même temps l’attaque et le corps du gong. Ceci donne un résultat hybride intéressant. On peut alors imaginer des combinaisons de sons métaphoriques et suggestifs, comme un nuage granulaire à partir de chants d’oiseaux filtrées par une voix.
3.- Filtres révérbérateurs.
Les filtres en peigne (comb filters) sont utilisés pour créer des effets de réverbération sur un signal sonore. Dans un filtre en peigne, le signal d’entrée pénètre une ligne de délai, puis, quand il arrive à la sortie, il est encore alimenté à l’entrée après avoir été multiplié par un facteur g. Le temps que prend le signal pour circuler à travers la ligne de délai est appelé temps de boucle (loop time). La réponse impulsionelle d’un filtre en peigne est un train d’impulsions espacées de manière équidistante à un intervalle analogue au temps du boucle. Cette réponse a une chute exponentielle déterminée par les valeurs choisies par le temps du boucle et par le facteur g.
L’effet de passage d’un filtre en peigne sur un signal sonore lui donne des caractéristiques réverbérantes; de plus, le signal à l’entrée pousse le filtre à résonner dans sa fréquence naturelle, en additionnant alors une composante spectrale au signal sonore d’origine (équivalent à la fréquence naturelle du filtre). La résonance du filtre a une enveloppe semblable à celle trouvée dans la plupart des sons de type cloche - il a une attaque rapide et une chute exponentielle beaucoup plus longue (Dodge., Jerse, 1985). On peut bien sûr avoir plusieurs filtres en peigne en parallèle, chacun avec une fréquence différente; ceci va créer la sensation auditive d’accords qui font résonner le signal à l’entrée.
On pourrait utiliser des filtres en peigne en parallèle pour filtrer des sons granulaires. J’ai utilisé l’algorithme du logiciel SYTER au GRM (le Groupe de Recherche de Musique à Radio France), mais toujours avec des sons de voix parlée ou de voix chantée, et j’ai obtenu des résultats musicaux très agréables; pourtant, je n’ai jamais imaginé le filtrage en peigne de sons trop complexes comme des nuages granulaires, probablement parce que j’imaginais que le résultat serait trop réverbérant, barbouillé et chaotique. Néanmoins, on pourrait peut-être obtenir avec deux ou trois filtres en peigne en parallèle des résultats musicaux acceptables.
Les filtres résonateurs du logiciel Turbosynth (Digidesign) sont semblables aux filtres en peigne. Avec ces filtres ont doit déterminer la fréquence à réverbérer, le niveau de rétro-alimentation (feed-back), la polarité (positive ou négative), et le mixage entre le signal d’origine et le signal réverbéré. Cet algorithme est très efficace; je l’ai utilisé pour créer plusieurs sons sur mes compositions électroacoustiques, mais je ne l’ai jamais utilisé pour filtrer des sons granulaires. Le seule problème avec cet algorithme est que l’on ne peut pas modifier les paramètres des filtres au cours du temps (fréquence, intensité, largeur de bande), tandis qu’avec l’algorithme des filtres en peigne du SYTER il est possible de le faire.
III.- D’autres applications des méthodes de synthèse traditionnelle aux formes d’onde des grains.
1.- L’amplitude modulée, la modulation en anneau et la modulation single-sideband.
Le concept de base de l’utilisation de l’amplitude modulée (AM) et de la modulation en anneau pour la génération des grains synthétiques est semblable à celui de l’utilisation de la modulation en fréquence (FM). L’idée essentielle est qu’avec très peu de données, on peut faire varier radicalement le contenu spectral de la forme d’onde du grain. Toutefois, la principale différence est qu’avec la FM on a besoin de deux fréquences sinusoïdales pures seulement pour générer des spectres riches. Donc, la FM est efficace pour la création de grains synthétiques. En revanche, si l’on veut affecter les grains d’un échantillon, la FM n’est pas appropriée, car on aura comme résultat un spectre excessivement dense. L’amplitude modulée, la modulation en anneau et la modulation single-sideband (d’une bande unique) sont plus appropriées pour altérer le spectre des grains d’un échantillon, puisqu’on a un moindre nombre de sidebands résultantes.
Dans un instrument typique d’amplitude modulée (Figure 6), l’oscillateur porteur (carrier) a une fréquence constante fc et l’oscillateur modulant a une fréquence fm . Si la forme d’onde de chaque oscillateur est une onde sinus, la sortie de l’oscillateur modulant est additionnée à la valeur qui exprime l’amplitude que l’oscillateur porteur tiendrait (s’il n’y avait pas de modulation). L’amplitude de l’oscillateur modulant est exprimé comme une proportion de l’amplitude non modulé de l’oscillateur porteur et elle est notée par la variable m, appelée index de modulation. Si m est égal à 0, il n’y a pas de modulation, et si m est égal à 1, alors on a une modulation à 100%. Quand l’onde porteuse et l’onde modulante sont des sinus, on a de l’énergie spectrale dans trois fréquences: la fréquence de l’onde porteuse (fc) , et les deux sidebands (fc + fm et fc - fm ). L’amplitude de la fréquence de l’onde porteuse ne varie pas avec l’index de modulation, tandis que l’amplitude des sidebands dépend d’un facteur de m/2 moins que l’amplitude de la porteuse. Donc, si m est égal à 1, l’amplitude des sidebands sera de la moitié de l’amplitude de l’onde porteuse (Dodge,. Jerse, 1985).
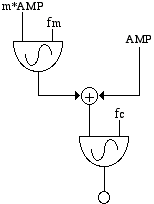
Figure 6.- Instrument d’amplitude modulée avec une onde sinus comme porteuse et une onde sinus comme modulante (Dodge et Jerse, 1985).
Comme le spectre obtenu avec deux ondes sinusoïdales est pauvre, l’utilisation de la AM serait plus efficace pour affecter le spectre des formes d’onde plus complexes. On pourrait utiliser soit des ondes avec plusieurs composantes sinusoïdales (Roads, 1985. Rocha Iturbide, 1994), soit des ondes complexes lues sur un échantillon. Prenons le premier cas et donnons un exemple d’un instrument granulaire avec le logiciel de Csound (Figure 7).
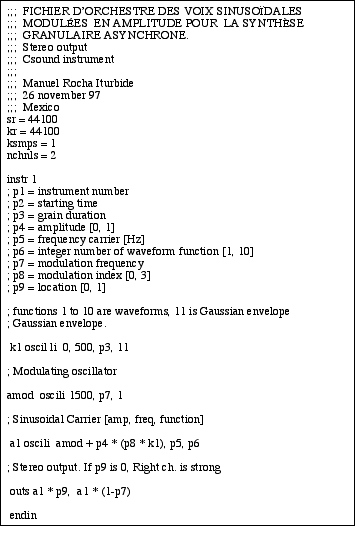
Figure 7.- Fichier d’orchestre des voix sinusoïdales modulées en amplitude pour la synthèse granulaire asynchrone.
Dans un instrument de ce type on peut affecter le spectre de la forme d’onde choisie (on a un fonction d’onde qui va de un à dix harmoniques) par la variation de la fréquence de l’onde porteuse, la fréquence de la modulante, et l’index de modulation. Toutefois, il nous suffirait d’utiliser toujours la même fonction d’onde, probablement celle de dix harmoniques pour avoir un spectre résultant de trente composantes de fréquence (dix de la porteuse plus les vingt sidebands).
Le seul problème qui se présente au moment d’effectuer la AM sur les grains est que l’index de modulation dépend de l’amplitude des grains; il y a donc une interaction qui n’est pas forcément souhaitable. Si l’on veut avoir une modulation il nous faut des grains forts, tandis qu’avec des grains de basse amplitude on n’aura pratiquement pas de modulation.
On peut aussi utiliser la AM pour affecter des sons échantillonnés, mais la modulation en anneau pourrait être mieux adaptée pour ceci, car la porteuse est éliminée, et il reste seulement les deux sidebands générés par la modulation (Figure 8). Il est parfois convenable d’avoir moins de sidebands, car la modulation d’un signal complexe peut donner trop de sidebands qui vont enrichir de manière excessive son spectre. L’effet résultant de la modulation en anneau est que si les composantes d’origine du son modulé ont un spectre harmonique, elles vont toutes disparaître, et on aura à leur place les deux sidebands produits par la modulation: fc + fm et fc - fm. Cet effet va produire la plupart du temps un spectre inharmonique. Dans le cas d’une voix par exemple, toutes ses composantes en fréquence seront transposées deux fois. Si on a une composante de 500 Hz, et la fréquence modulante est de 33 Hz, la composante originelle de la voix disparaîtra et deviendra deux nouvelles composantes à 533 Hz et à 467 Hz. Si ce signal a 100 composantes en fréquence, on aura comme résultat un signal de 200 composantes dont aucune ne gardera sa fréquence d’origine. Le danger dans ce cas est que la voix peut devenir méconnaissable, pourtant, si l’on contrôle les effets inharmoniques obtenus ils seront au moins musicaux.
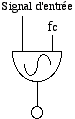
Figure 8.- Altération du spectre d’un signal par modulation en anneau.
Étudions maintenant un exemple d’un instrument de synthèse granulaire à partir d’échantillons, avec la modulation en anneau de ses grains (Figure 9). Dans cet instrument il n’y a pas autant de variables qu’avec la modulation AM avec des grains synthétiques; en fait, on n’a même pas d’index de modulation. Le seul paramètre que l’on peut changer pour modifier le spectre des grains est la fréquence de l’oscillateur qui fonctionne comme porteuse. Toutefois, différents effets harmoniques et inharmoniques peuvent être éteints par la simple modification de ce paramètre (dans l’orchestre de Csound , il est représenté par la variable p6). Dans cet instrument granulaire, la variation de l’amplitude des grains ne modifie pas l’amplitude les sidebands.
Un synthétiseur granulaire avec modulation en anneau peut économiser beaucoup de travail au compositeur qui veut transformer le spectre des grains issus des sons instrumentaux. Pour donner un exemple, quand je réalisais des nuages granulaires en partant des instruments à cuivre pour la réalisation de ma composition Transiciones de Fase, je voulais produire une transformation graduelle du spectre des grains d’une attaque de trompette. J’ai dû alors copier plusieurs fois l’échantillon de l’attaque de la trompette, et puis j’ai altéré le spectre de chaque échantillon de manière graduelle vers les partiels aigus avec un pitch-shifter, (une technique qui effectue la modulation d’une bande-unique). Puis, j’ai effectué la synthèse granulaire avec mon système de Csound-Patchwork en changeant de la lecture d’un groupe d’échantillons à l’autre (toujours allant vers les échantillons plus aigus) avec l’utilisation de deux tendency masks. En fin, si j’avais imaginé à ce moment-là la possibilité d’utiliser la modulation en anneau de façon simultanée à la synthèse granulaire, j’aurais pu transformer le spectre des grains plus facilement et économiser le temps de préparation des différents échantillons. Cependant, pour les besoins spécifiques de la transformation spectrale dont je viens de parler, j’aurais dû plutôt réaliser l’application d’un pitch-shifter, car l’avantage de celui-ci sur la modulation en anneau est qu’on change chaque fréquence du spectre du signal sonore à l’entrée en additionnant une constante, sans augmenter pour autant le nombre des composantes spectrales. Avec le pitch-shifter on change seulement le rapport entre les composantes harmoniques, mais ceci rend aussi le spectre inharmonique. En outre, avec la modulation en anneau, la transposition s’effectue au-dessus et au-dessous de la fréquence de chaque composante en même temps, et donc, il n’est pas possible d’effectuer une progression continue et pure vers le registre aigu ou vers le registre bas. Le seul problème avec la modulation d’une bande unique (single-sideband modulation), caractéristique du pitch-shifter, est que son application à un système informatique est très compliquée du point de vue technique (Dodge., Jerse, 1985).
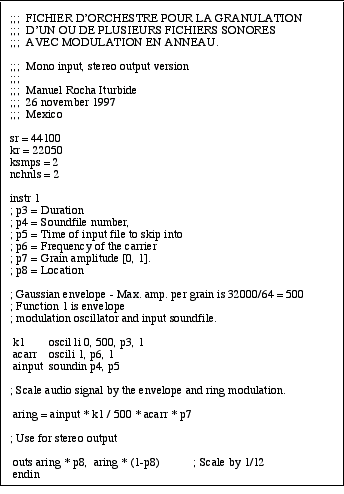
Figure 9.- Fichier d’orchestre pour la granulation d’un ou de plusieurs fichiers sonores avec modulation en anneau.
2.- Waveshaping.
Waveshaping est une méthode de synthèse avec laquelle on peut générer des spectres avec une évolution dynamique de ses composantes (comme avec la FM). Un waveshaper effectue la distorsion de l’amplitude d’un son et produit une altération de sa forme d’onde avec un subséquent enrichissement de son spectre. La caractéristique principale d’un waveshaper est que le spectre qu’il produit change avec l’amplitude du son car il constitue un processeur de caractère non linéaire.
Un waveshaper utilise une fonction de transfert (transfer fonction) qui met en rapport l’amplitude du signal à la sortie avec l’entrée. La fonction de transfert nous permet de prédire le changement du spectre de la forme d’onde à l’entrée du waveshaper à partir de sa valeur d’amplitude. Une fonction de transfert non linéaire pourrait être F(x) = x3 , où la valeur de chaque échantillon à l’entrée est multipliée au carré au moment de passer à la sortie (Dodge., Jerse, 1985).
Comme avec la FM, le waveshaping bénéficie d’un contrôle continu du spectre par l’utilisation d’un index de modulation, ce qui rend possible la variation du spectre à travers le temps par la simple modification de la valeur d’index. La principale différence avec la FM est qu’avec le waveshaper il y a un rapport entre la variation d’amplitude de la forme d’onde et le spectre. Cette caractéristique fait qu’il soit utilisé pour simuler des sons d’instruments cuivrés, où une augmentation d’amplitude d’une attaque enrichit automatiquement le spectre du son.
Je ne peux pas décrire en détail la possible application d’un waveshaper sur un système de synthèse granulaire, car la formalisation et le contrôle des fonctions de transfert sont assez complexes. Toutefois, il serait intéressant que quelqu’un le fasse, car on pourrait bénéficier d’un outil puissant pour transformer le timbre des grains à partir d’une onde sinusoïdale et du paramètre de l’index de modulation. Cependant, si l’on utilise un waveshaper pour effectuer des évolutions granulaires de timbre, il faudra contempler aussi la variation obligatoire des amplitudes des grains, et donc, on aura certaines limitations, car avec des grains faibles en amplitude le spectre sera toujours pauvre, et avec des grains forts le spectre sera toujours riche. Alors, cette application servira seulement pour la réalisation des nuages granulaires avec une esthétique spécifique reliée par exemple au fonctionnement des sons de type cuivré.
3.- Hybridation et sophistication des techniques pour la génération des formes d’onde des grains.
L’imagination du compositeur et ses besoins spécifiques seules peuvent déterminer les différentes combinaisons des techniques pour la génération des formes d’onde des grains. Néanmoins, certaines techniques exigent des formes d’onde simples, tandis que d’autres exigent de formes d’onde complexes, et donc, ceci va contribuer aussi à la détermination du mixage des techniques. Pour donner un exemple, la FM a besoin des formes d’onde simples, et il serait donc absurde d’utiliser des échantillons complexes ou des ondes complexes crées par un waveshaper; en revanche, on pourrait employer des formes d’onde additives avec un nombre limité de composantes spectrales (de 1 à 10 par exemple) comme porteuses. D’autre part, les formes d’onde avec un spectre dense comme ceux qui sont générés par la FM ou par le waveshaper pourraient par exemple être utilisés pour être filtrés avec des filtres résonateurs ou même avec des filtres substractifs.
On a parlé des différentes applications de synthèse granulaire qui ont utilisé la FM (Truax, 1987. Jones et Parks, 1988). Toutefois, la FM est une technique assez complexe qui peut avoir plusieurs configurations différentes, et je suis sûr que beaucoup d’elles n’ont pas été employées jusqu’à ce jour pour la synthèse granulaire; pour donner quelques exemples: il y a des instruments FM avec porteuse double ou multiple (Dodge., Jerse, 1985. Roads, 1994) utilisés pour créer des régions formantiques dans le spectre; il y a des instruments FM avec modulateur multiple, où plusieurs oscillateurs modulent une seul oscillateur porteur; il y a des instruments FM avec feed-back (rétro-alimentation) (Roads, 1994), etc. Ces différentes configurations pourraient être essayées pour générer la forme d’onde des grains, avec l’avantage que leur formalisation n’est pas très compliquée.
Il y a beaucoup d’autres techniques pour la génération d’ondes synthétiques et pour le traitement du signal des grains qu’on n’a pas mentionnées ici. Une étude étendue serait trop longue et n’aurait pas de place dans cette thèse. Ce qui m’a intéressé dans cette section est de donner des exemples, des idées, et un aperçu de l’ampleur des possibilités pour la génération ou l’affectation des formes d’onde des grains, en espérant que de futurs compositeurs et chercheurs puissent envisager la création de nouvelles méthodes, soit par l’utilisation de nouvelles techniques ou par le mélange de différentes méthodes étudiées ici; bien évidemment, la manière de réaliser cette tâche dépendra de la façon alchimique de "cuisiner" les transformations sonores de chaque personne.