FOOTNOTES ON THIS CHAPTER ARE NOT YET IMPLEMENTED!
CHAPITRE VI: LES ALGORITHMES DE CONTRÔLE
ET LA SYNTHÈSE GRANULAIRE.
I.- Concepts de base pour le contrôle de la synthèse granulaire.
"On peut créer des complexes sonores à partir de la matière première du son, le son sinus (ou de ses remplaçants de type de Gabor), complexes sonores aussi riches que les sons naturels, avec des évolutions maîtrisées scientifiquement et sur des plans très généraux abstraits".
Iannis Xenakis, 1971.
La caractéristique essentielle de la synthèse granulaire en général (mise à part la granulation par analyse-synthèse) est la simplicité conceptuelle de son mécanisme de base: avec des petits fragments du son, soit des "particules élémentaires", on peut créer des structures sonores complexes. Le degré de sophistication d’une application de synthèse granulaire dépend de la façon dont ce concept de base est appliqué, du choix d’une plate-forme de synthèse, et de la manière d’exercer le contrôle sur elle (Eckel et Rocha Iturbide, 1995). D’autre part, la nécessité de produire des milliers de grains par seconde nous oblige à envisager l’utilisation des opérations algorithmiques pour déterminer l’évolution des grains dans le temps.
1.- Le micro-temps et le macro-temps.
Le contrôle des grains peut opérer sur différentes échelles temporelles, et permet la structuration musicale du son au niveau spectrale (timbre) ou harmonique, et au niveau temporel ou rythmique. La possible utilisation de structures semblables sur différentes échelles temporelles agit sur différents domaines de la perception, et ceci a constitué une source riche pour l’imagination du compositeur (Stockhausen, K. 1959). Les techniques granulaires ont prouvé qu’elles étaient bien efficaces pour exploiter ce principe de perception. D’ailleurs, la double nature de la perception vers des structures sonores dans le champ temporel et dans le champ fréquentiel a favorisé les premières idées pour la création de la synthèse granulaire (Gabor, D. 1947).
Dans les différents chapitres de cette thèse, j’ai décrit les différentes techniques de synthèse granulaire qui existent, et nous avons vu comment quelques-unes étaient plus adaptées au domaine du micro-temps et d’autres au domaine du macro-temps. J’ai crée un modèle de synthèse granulaire formantique bien adapté pour travailler dans les deux domaines (Eckel et Rocha Iturbide, 1995), et j’ai proposé la création de techniques granulaires hybrides qui pourraient bénéficier aussi bien le domaine spectral que le domaine temporel (voir deuxième et troisième chapitres). Dans ce chapitre je voudrais encore souligner le besoin de développer des techniques de synthèse granulaire globales qui fonctionnent sur les différentes échelles temporelles, même si certaines d’entre elles ont le défaut de ne pas se servir de l’analyse, car on peut tout de même les utiliser pour la composition. Stockhausen et Xenakis sont deux compositeurs contemporains reconnus qui font valider cette idée. Le premier a étudié et expérimenté avec le rapport entre le son et la musique, et il a imaginé une méthode de composition de timbre en utilisant des rythmes qu’il appelle phase duration (durée de phase). Stockhausen a établi une connexion entre les micro-structures et les macro-structures musicales au moyen de l’élément temporel du rythme (Stockhausen, 1959). C’est d’ailleurs la même philosophie que Gerhard Eckel et moi-même avons suivie pour la modélisation de l’outil de synthèse GiST (Eckel et Rocha Iturbide, 1995) (voir quatrième chapitre). D’autre part, Xenakis a proposé une méthode de synthèse à partir de "grains élémentaires" et il a suggéré d’utiliser des méthodes macroscopiques pour les contrôler, mais en privilégiant autant le grain comme entité individuelle que comme entité appartenant à un groupe complexe:
"...c’est ce qui nous intéresse en particulier, agir comme architectes sur la matière sonore pour construire des sons complexes et des évolutions de ces êtres, ce qui signifie qu’il faut utiliser des méthodes d’analyse et de construction macroscopiques. Les micro-sons, les grains élémentaires n’ont pas d’importance à l’échelle où nous nous plaçons. Seuls les groupes de grains et les caractéristiques de ces groupes ont un sens. Naturellement dans les cas tout particuliers, le grain unique sera rétabli dans sa gloire. Dans une chambre de Wilson c’est la particule élémentaire qui porte la physique théorique et expérimentale sur ses épaules et dans le soleil c’est l’ensemble des particules et leurs inter-réactions denses qui font l’objet soleil." (Xenakis, 1971).
Il y a peut-être ici une tendance de Xenakis à favoriser le travail de composition dans le macro-temps, mais sa méthode granulaire va bénéficier aussi au travail de composition dans le micro-temps. Xenakis a été conscient de l’importance d’unifier le travail de composition dans le niveau micro et dans le niveau macro, et quelques années plus tard il va créer un programme informatique pour la création des œuvres instrumentales au moyen de formules de probabilité interconnectées, et de fonctions qui rendent possible leur combinaison:
"Ce programme (ST) peut déterminer la pièce simultanément dans un niveau ‘minimal’ (je réserve l’utilisation du mot ‘microscopique’ pour la synthèse sonore), disons à chaque seconde, ainsi que dans le niveau macro, c’est-à-dire, à chaque minute, ou même toutes les 10 minutes ou sur des périodes plus longues." (Xenakis dans Varga, 1996).
L’idée d’avoir une méthode de synthèse globale pour pouvoir réaliser une composition entière sans avoir recours à un outil de mixage est peut-être utopique; certains estiment que les "méthodes macroscopiques" ne font pas partie de la synthèse, mais qu’elles sont des mécanismes de contrôle externe (Vaggione, 1993). Toutefois, je crois que ces méthodes sont inhérentes à la synthèse granulaire et qu’avec elles on peut réussir à créer des compositions d’une certaine esthétique également inhérente aux techniques granulaires. Néanmoins, si l’on veut faire de la synthèse granulaire un "lapis philosophale" pour avoir un contrôle parfait autant dans le domaine spectral que dans le domaine temporel, alors là, il y a des limites; dans ce cas il faudra développer les techniques d’analyse-synthèse ou les hybrider, comme je l’ai proposé au troisième chapitre.
2.- L’évolution des méthodes algorithmiques dans la musique par ordinateur.
La nécessité d’utiliser différents types d’algorithmes pour contrôler l’évolution des grains au cours du temps conditionne le résultat esthétique de la synthèse granulaire. Nous allons faire un parcours historique rapide du développement des méthodes algorithmiques utilisées dans la musique par ordinateur, pour avoir une vision plus globale et pouvoir comprendre les différentes tendances qui existent actuellement pour le contrôle des quanta sonores dans les techniques de synthèse granulaire.
Avec l’apparition des ordinateurs et le conséquent développement de l’intelligence artificielle, les musiciens ont essayé d’introduire l’intelligence musicale dans les machines pour imiter certains aspects de l’intelligence musicale humaine, au moyen de la programmation par ordinateur. Des pionniers tels que Lejaren Hiller (1959) ont construit des programmes qui simulaient un style musical donné, par la création de collections de règles musicales empruntées des paradigmes musicaux existants et en utilisant des contraintes pour filtrer la sortie (output) d’un générateur aléatoire de nombres. Ces collections de règles pourraient être nommées "grammaires" compositionnelles par analogie avec un langage naturel (Risset, 1989). Hiller a essayé d’utiliser différents types de "grammaires" pour imiter des styles musicaux tels que le contrepoint du dix-huitième siècle. Néanmoins, ces essais n’ont pas abouti à un bon résultat musical, puisque les processus de composition ne fonctionnent pas par le simple filtrage des choix randomisés à travers une collection de règles d’exclusion (Risset, 1989). Faire apprendre à un ordinateur des règles musicales et à effectuer des choix en partant de certaines contraintes est faisable, mais on ne peut pas dire que le résultat sera artistique. Toutefois, ces premiers essais ont été fondamentaux pour les développements subséquents d’intelligence artificielle dans le domaine de la composition musicale.
Des années plus tard, d’autres "grammaires" ont été essayées; Iannis Xenakis a travaillé avec la programmation des règles statistiques (1971). Ces règles spécifient la composition de manière globale plutôt que dans ses détails au moyen de distributions statistiques, tout en ayant certains contraintes des choix aléatoires des éléments. Ce procédé, nommé stochastique, a bien fonctionné, car le but n’était pas d’imiter des styles musicaux, mais de créer de nouveaux styles avec des grammaires nouvelles.
La composition par règles au moyen de l’ordinateur s’est davantage développée dans les années soixante-dix, et a débouché sur les systèmes basés sur des règles (rule-based systems) et sur la programmation orientée par objets (object oriented programming). Ces méthodes beaucoup plus sophistiquées que leur ancêtres ont encore gardé l’élan d’imitation des styles musicaux préexistants, mais des "grammaires" nouvelles ont été également développées, qui ont donné comme résultat des compositions avec un haut niveau d’abstraction musicale (Barlow, C. 1988). Les caractéristiques principales de ces méthodes sont: une spécification graduelle des objectifs; le besoin d’une définition claire et d’une description concise d’un problème donné; et la reconstruction du comportement humain pour la résolution de problèmes au moyen d’un programme qui raisonne et qui cherche à travers un espace symbolique (Beyls, 1991). D’autre part, la philosophie de ces méthodes a favorisé le développement du champ de la composition interactive, où on dispose d’une série de règles, mais en même temps on laisse des voies ouvertes pour la perception et l’interprétation d’une influence extérieur au système.
L’habileté de l’ordinateur pour manipuler une grande quantité de données, et le développement de nouveaux langages de programmation appropriés pour la composition musicale, a incité les compositeurs à aller au-delà de l’imitation des règles anciennes, en les combinant et en les transformant de façon complexe, ou en créant des règles complètement nouvelles. Selon J.C Risset, les syntaxes nouvelles ont toujours de la peine à être assimilées par le public, et elles prennent toujours du temps pour être digérées. Ce délai naturel dans tout art contemporain, plus l’excessive rapidité de l’évolution des langages artificiels, ont favorisé à plusieurs occasions la création d’œuvres musicales que nous ne savons plus comment juger. Sont-elles des œuvres incohérentes, non-musicales, ou parfois peut-être des œuvres géniales avec une esthétique qu’on est incapable de comprendre?. La seule chose vraie est que "les œuvres d’art font des règles, mais les règles ne font pas des œuvres d’art". Avec les ordinateurs il faudra toujours faire attention, car on peut rapidement aller au-delà de notre capacité d’assimilation si on surcharge un programme de règles sans avoir des fondations conceptuelles pour maintenir intègre notre langage syntactique.
A partir des années quatre-vingt, des méthodes algorithmiques nouvelles s’ont apparues dans le champ musical grâce à l’application de la théorie du chaos (Degazio 1986, Dodge 1988), ainsi que d’autres systèmes dynamiques complexes non-linéaires tels que les automates cellulaires (Beyls, 1989). Beyls appelle ces méthodes "sub-symboliques" (subsymbolic methodes), car elles utilisent des représentations analogiques qui gardent implicitement ce qu’elles reproduisent dans leur représentation. Ces méthodes ont une approche béhavioriste en opposition aux systèmes basés sur des règles qui adhèrent aux stratégies basées sur la connaissance (knowledge-based) pour la solution de problèmes donnés. Ces dernières méthodes sont appelées "symboliques". (Beyls, 1991).
Grâce à plus de vingt ans d’études et de recherches dans la nouvelle science du chaos, aujourd’hui tout le monde sait qu’une grande partie de phénomènes dans la nature peuvent exhiber un comportement complexe et chaotique, inclus certains systèmes déterministes comme le pendule. Nombreux phénomènes chaotiques ont en plus un comportement fractal (Gleick, 1987), c’est-à-dire, qu’ils possèdent des éléments qui se répètent à travers différentes échelles. Cette caractéristique a attiré beaucoup de compositeurs, car on sait que dans la musique en général il y a parfois des structures semblables qui se répètent sur différentes échelles, comme ce peut être par exemple le cas de la variation d’un motif rythmique ou mélodique dans une fugue de Bach ou dans un raga Indien. D’autre part, certains phénomènes chaotiques non-linéaires se présentent dans plusieurs instruments de musique comme par exemple, la production de multiphoniques dans les instruments de vent en bois, ou avec la formation de régions de turbulence dans le corps de la flûte.
La complexité et la beauté de certains processus de la nature, et la possibilité de les décrire au moyen des équations mathématiques issues de la théorie du chaos, a induit les compositeurs et les artistes d’autres disciplines à se servir d’elles pour la création d’œuvres d’art. De plus, dans les phénomènes chaotiques les éléments se comportent soit de façon indéterminée, soit de façon déterminée, et le mélange de ces deux tendances constitue une opposition dialectique riche et bénéfique pour la composition musicale. D’autre part, l’évolution des systèmes dynamiques non-linéaires dans la théorie du chaos produit des orbites complexes très intéressantes, et ces orbites dépendent d’un phénomène appelé "dépendance sensible aux conditions initiales". Ces conditions initiales peuvent être infinies, et par conséquence les orbites aussi (Bidlack, 1992). Donc, on peut avoir avec une seule équation une grande richesse d’information qui va toujours varier en dépendant des données initiales.
En regardant les possibilités issues des équations de la théorie du chaos qu’on vient de mentionner, nous nous rendons compte de la richesse qui existe sur ce terrain, et des avantages qu’on pourrait avoir pour le contrôle de la synthèse sonore, ainsi que pour le contrôle des éléments musicaux dans la composition algorithmique. Certains avantages de ces méthodes par rapport aux méthodes "symboliques" sont les suivants: avec des équations simples on peut avoir des résultats complexes; leur "grammaire" est déjà organique et cohérente puisqu’elle est déduite des lois de la nature (tandis que les "règles" des systèmes "symboliques" pourraient facilement devenir artificielles); et que cette "grammaire" s’adapte bien à la musique puisque les structures fractales sont semblables à certains processus créatifs hiérarchiques. Il y a d’autres avantages plus particuliers pour le cas spécifique de la synthèse granulaire, mais on les étudiera un peu plus tard.
Les méthodes "subsymboliques" présentent aussi des risques et des défauts. Le fait que certains équations du chaos simulent la complexité de la nature et donnent des géométries fractales intéressantes ne signifie pas qu’on peut tout simplement transposer ces géométries dans le domaine musical et avoir une œuvre artistique. Selon Jaques Mandelbrot, les images fractales obtenues par un algorithme peuvent être belles, de la même manière que les "objets trouvés" peuvent être beaux, mais elles ne peuvent pas être considérées comme s’il s’agissait de l’art (Risset, 1989). Le problème majeur de ces méthodes est qu’elles sont belles dès le départ, et que si on n’effectue pas des altérations importantes, le résultat peut devenir à la fin trop reconnaissable et ennuyeux. D’autre part, il faut décider comment choisir la meilleure transposition des données des équations sur un plan musical, et très souvent, on a la sensation d’avoir trop des contraintes, et que les équations sont plus importantes que nous. En conclusion, avec les méthodes "symboliques" nous avons un rôle plus créateur au moment de les modéliser, et la combinaison des différents éléments dépend de nous, tandis que les méthodes "subsymboliques" sont dès le départ plus puissantes, car une simple équation peut définir l’esthétique entière d’une composition, et nous restons un peu en dehors, en modifiant simplement les paramètres qui vont changer le contour du processus, mais pas son essence.
Dans ce chapitre, je étudierai les opérations algorithmiques appartenant à ces deux groupes de méthodes, et j’analyserai les avantages et les désavantages de chacune pour le contrôle de la synthèse granulaire (aussi bien dans le micro-temps que dans le macro-temps), ainsi que les conséquences esthétiques de leur utilisation; je proposerai aussi une possible hybridation de méthodes qui pourrait nous conduire à avoir un contrôle de la synthèse granulaire beaucoup plus sophistiqué; finalement, on étudiera les différents degrés d’interaction qu’on peut avoir sur un système de synthèse granulaire, ainsi que l’influence de cette interaction sur le résultat musical du système de contrôle.
Avant de conclure ce rapide parcours historique je voudrais parler un peu des automates cellulaires. Ces algorithmes "subsymboliques" reproduisent l’interaction locale de beaucoup d’agents qui participent, mais où il n’y a pas de superviseur. Cette image constitue une claire métaphore des insectes tels que les fourmis et les abeilles. Or, on sait que beaucoup de sons de synthèse granulaire sont semblables aux bruits de ces insectes, et que le fait même d’avoir des milliers de grains constitue une analogie proche. Il serait intéressant d’étudier les comportements de certains animaux dans la nature, même si on ne connait pas de représentations mathématiques les décrivant, car ils constituent tout de même des métaphores qui peuvent nous inspirer et nous guider pour construire des sons complexes qui évoluent d’une manière semblable. En fin de compte, comme l’exprime J.C. Risset: "J’ai été impressionné par le domaine du chaos, et j’ai fait référence à lui dans diverses pièces, au moyen des métaphores musicales programmatiques" (Risset, 1989). Ce qui est important est de trouver l’inspiration dans la complexité de la nature, et de pouvoir utiliser les règles et les algorithmes, mais de rester libres pour pouvoir les transgresser.
3.- Déterminisme et Indéterminisme.
"La caractéristique dynamique la plus importante d’un ‘système ouvert’ quantique de Prigogine est qu’il est positionné délicatement sur une ligne disjonctive critique entre le statisme et le chaos. Prigogine décrit cette caractéristique comme: ‘loin des conditions d’équilibre’. S’il y a moins d’énergie qui passe à travers le système il s’arrêtera et la matière attrapée dedans deviendra inerte, sans ordre ni sens. S’il y a plus d’énergie le système tournera dans un état trop turbulent, et il y aura comme conséquence du simple ‘bruit’."
Danah Zohar (1990).
Imaginons le binôme polaire suivant: sur un extrême, on a une onde sinusoïdale pure parfaitement périodique, et sur l’autre extrême on a du bruit blanc. Ces deux pôles sont curieusement très semblables, l’onde périodique infinie ennuie, tandis que le bruit blanc suscite de la confusion. L’entropie se trouve bien sûr du côté du désordre, dans l’extrême du bruit blanc, mais l’incessante périodicité de la forme d’onde est aussi dans un certain sens un état d’entropie, au moins du point de vue de notre perception auditive. Or, n’importe quel état intermédiaire entre onde pure et bruit blanc est un état avec un certain degré d’intérêt, et on peut avoir virtuellement tous les sons existants entre ces deux pôles, certains plus déterministes et avec moins d’entropie, et certains autres plus indéterminés et avec davantage d’entropie.
On pourrait dire que la synthèse granulaire se trouve dans cet espace bipolaire (déterminisme et indéterminisme), car comme on l’a déjà mentionné, le fait d’avoir des milliers de grains dans une seconde nous oblige à chercher des mécanismes de contrôle algorithmiques, c’est-à-dire, des équations mathématiques qui peuvent être déterministes (le lancement périodique des grains), indéterministes (le lancement aléatoire des grains), ou un mélange des deux.
Iannis Xenakis, le premier compositeur à concevoir l’utilisation des "quanta sonores" pour la composition musicale, a encadré cette technique de synthèse dans le plan dialectique ordre-désordre.
"Lorsque nous disons ordre ou désordre, nous sous-entendons d’abord ‘d’objets’, ‘d’éléments’ puis, et c’est déjà plus complexe, nous définissons les ‘éléments’ mêmes’ dont nous voulons étudier et construire l’ordre ou le désordre, leur échelle par rapport à la nôtre, puis nous qualifions et nous nous efforçons de mesurer cet ordre ou désordre". (Xenakis, 1971).
Avec ce binôme, Xenakis essaie de définir des phénomènes naturels analogues aux processus sonores possibles tels que le déplacement des molécules de gaz. Il va utiliser aussi le concept d’entropie. L’entropie pour lui est "la quantité d’ordre ou de désordre définissable dans un groupe d’éléments". Une entropie nulle est équivalente à notre onde sinusoïdale, et peut être représentée par un seul grain (avec une forme d’onde sinusoïdale) produit à intervalles de temps réguliers, tandis qu’une entropie moyenne maximum (théoriquement •) est équivalente à notre bruit blanc, ou à une distribution aléatoire des grains sur le terrain temps-fréquence. Les transitions entre différents types d’ordre (entropie minimale) et différents types de désordre (entropie maximale) et à l’inverse, constituent les opérations musicales possibles, et selon Xenakis, toute musique existante pourrait être reproduite entre ces deux extrêmes au moyen de différentes distributions de grains.
Le concept d’ordre et de désordre est également substantiel dans la théorie du chaos. Cependant, le chaos ne représente pas le désordre total, mais des états de complexité avec une certain degré d’indétermination situés entre l’ordre et le désordre. Donc, soit avec des opérations statistiques, soit avec des équations de chaos, d’algorithmes d’automates cellulaires, ou avec n’importe quel algorithme qui effectue certaines opérations avec un degré d’indétermination, nous sommes sur le territoire décrit par Prigogine, un territoire d’équilibre précaire où il y a des fluctuations entre ordre et désordre. Les techniques de contrôle de la synthèse granulaire se trouvent aussi dans un territoire semblable; il faudra donc tenir compte de ce fait, ainsi que des conséquences esthétiques au moment de s’en servir. Néanmoins, on pourrait réaliser des opérations algorithmiques d’ordre total ou de désordre total, mais alors, ce serait limitant et absurde et on ne profiterait plus de la richesse des possibilités musicales et de la complexité qui se trouve entre les deux extrêmes. Il faut dire que la physique quantique a été à l’origine du développement des philosophies esthétiques où on utilise un certain degré d’indétermination, et curieusement, les techniques de synthèse granulaire sont essentiellement quantiques. Donc, il faudra d’autant plus tenir compte de ces principes. Néanmoins, il faudra aussi faire toujours attention avec le facteur d’indétermination, puisqu’il peut facilement créer de l’incohérence. Dans une œuvre d’art, il doit toujours exister un degré d’intégrité et de cohérence entre ses différentes parties constitutives. Une manque d’intégrité provoquerait l’éclatement de l’ensemble en morceaux, et il deviendrait éventuellement du bruit, tandis que trop de cohérence ferait que l’ensemble devient une structure semblable à d’autres structures déjà existantes, et il ne pourrait pas se tenir par lui-même (Yadegari, 1991). Il faudra donc toujours trouver un équilibre entre ordre et désordre.
4.- Automatisme et Geste.
Tous les compositeurs qui ont travaillé avec des ordinateurs ont été, une ou plusieurs fois, fascinés par l’idée de transformer la machine en créateur:
"Nous nous trouvons en face d’une tentative, objective si possible, de créer un art automate, sans l’interférence d’aucun être humain, à l’exception - comme dans le cas de Demiurgos dans Plato’s Politikos, ou de Jahve dans la bible Hébraïque et même du néant dans la théorie du Big Bang - du début, pour pouvoir donner l’impulsion initiale et quelques prémisses" (Xenakis, 1991).
L’automatisme peut être conditionné, la machine étant alors un reflet de notre élan créatif, mais on a eu parfois aussi la curiosité de planter une semence qui pourrait générer des processus inouïs et imprévus. La question se pose toujours: est-ce qu’un automate peut faire de l’art?. Je crois que dans la mesure où l’homme doit forcément intervenir pour programmer l’automate, il est possible que l’automate fasse de l’art, mais ce serait peut-être un art un peu limité, qui fonctionnerait seulement dans certains contextes. Tout dépend finalement de comment on programme l’ordinateur, mais aussi des algorithmes utilisées.
Quand on parle d’automatisme il faut distinguer différents degrés de responsabilité entre la machine et l’homme. On a d’abord des processus automatiques qui ne comportent pas d’opérations aléatoires, comme c’est le cas actuellement d’un outil de mixage (Protools), où l’on peut affecter des changements d’amplitude, de filtrage dynamique, etc, au moyen des enveloppes. Dans la synthèse granulaire asynchrone, les processus automatiques ont un caractère moins déterministe, car on utilise des tendency masks qui contrôlent les grains de manière aléatoire mais dans des limites très définies. Ici, le résultat global des sons sera toujours très semblable, et on aura encore un contrôle assez précis. Mais on pourrait également demander à l’ordinateur de manipuler de façon aléatoire un paramètre décisif dans la synthèse, comme par exemple l’index de modulation dans la synthèse FM (Chowning, 1973). Dans ce cas, le résultat changerait de façon drastique à chaque fois. L’ordinateur aurait un rôle plus déterminant.
En dehors des différents degrés de responsabilité dans la programmation automate, il faut tenir compte de la possibilité d’intervention de l’extérieur pour altérer ou transformer les processus programmés à l’avance. Ici on rompt le rythme des processus générés par l’ordinateur ou préétablis par nous pour entrer dans le domaine de l’interprétation ou de l’improvisation; il s’établit un dialogue entre l’ordinateur et nous.
Le geste musical humain produira toujours quelque chose de différent au niveau musical. Tous les compositeurs électroacoustiques se souviennent des jours où le mixage se faisait manuellement par obligation; il fallait apprendre à maîtriser le contrôle des canaux multiples (faders), plus les boutons de filtrage, etc. Cette façon de mixer devenait la même chose qu’apprendre à jouer d’un instrument, où les gestes musicaux (même si ils étaient planifiés) avaient des nuances différentes dans chaque session de mixage.
Un équilibre intéressant pourrait être établi au sein du contrôle algorithmique de la synthèse granulaire si on mélangeait automatisme et geste. Ceci est courant dans différents contextes musicaux: le performance, l’improvisation, les installations interactifs, et la musique électroacoustique interactive (voir fin du deuxième chapitre). Tout dépend de notre but esthétique. J’avais un projet pour adapter le programme de synthèse granulaire formantique GiST (Eckel et, Rocha Iturbide, 1995) à un interface midi qu’on manipule avec les mains, construit par Michel Waisvisz au studio STEIM en Hollande. Pour ceci, il aurait fallu construire un module particulier pour pouvoir manipuler les différents paramètres de la synthèse granulaire en temps réel, et programmer aussi des événements préexistants qu’on pourrait déclencher et faire varier à chaque fois.
II.- Contrôle stochastique.
"Stochastique (Gr. stochos = but). Terme emprunté par Xenakis à la théorie de la probabilité, où il dénote un processus dans lequel les différents pas sont gouvernés par des règles de probabilité. Il est possible par exemple, que chaque élément nouveau soit mené d’une certaine façon par tous les autres qui ont déjà eu lieu; ceci est le cas d’une chaîne de Markov. Très tôt dans ce processus, quand il y a encore une histoire courte d’événements, le degré d'aléatoire sera haut mais il décroîtra progressivement et alors le processus aura une tendance vers un objectif"
Griffiths, 1986.
Au milieu des années cinquante, il y a eu une réponse contre le haut degré d’abstraction de la nouvelle musique sérielle, qui avait une structure complexe mais peu musicale due à son caractère "artificiel". Xenakis a introduit alors les notions de ‘phénomènes statistiques’ et de ‘probabilité’, prises de lois stochastiques mathématiques pour décrire des phénomènes qui peuvent être définis globalement mais non dans leurs détails (tels que le choc de la pluie sur des surfaces dures, ou le chant des cigales dans un champ en été).
Les équations stochastiques peuvent simuler certains phénomènes naturels; pour cette raison, leur utilisation dans la musique donne lieu à des processus sonores semblables qui ont un caractère organique. L’association entre des phénomènes naturels tels que les déplacements de milliers d’hommes sur une place, et des particules sonores qui bougent dans le temps, est presque naturelle. Xenakis a été mené à utiliser des équations statistiques (prises de la théorie de la probabilité) pour le contrôle des particules dans la synthèse granulaire, car il n’est pas possible de s’occuper du contrôle individuel de chaque grain; quand on a une grande quantité de particules, il faut nécessairement avoir un contrôle statistique global.
J’ai déjà analysé dans le premier chapitre le système de composition granulaire de Xenakis (Xenakis, 1971), basé sur une série de trames où les grains sont distribués selon différentes lois stochastiques. Dans ce chapitre, j’analyserai les différentes opérations mathématiques qu’il réalise avec ces trames pour générer un son ou une composition complète. D’autre part, j’ai déjà analysé différentes méthodes stochastiques de contrôle qui ont été utilisées par plusieurs compositeurs pour l’application de la synthèse granulaire. Néanmoins, on étudiera certains aspects de ces méthodes en profondeur, ainsi que d’autres algorithmes à caractère stochastique pas encore analysés.
1.- Le système de trames de Xenakis.
"Par stochastique, Xenakis se réfère à un monde de masses sonores, de groupes vastes d’événements sonores, de nuages et de galaxies gouvernés par des caractéristiques nouvelles telles que densité, degré d’ordre, taux de changement, et qui requièrent des définitions et des réalisations au moyen de la théorie de la probabilité....Xenakis décrit un processus stochastique au moyen d’une analogie où les nuages de pluie sont perçus comme une distribution statistique de particules".
Dodge et Jerse, 1985.
Reprenons un peu les bases de la théorie de composition granulaire de Xenakis. L’instant t de la vie d’un son complexe durant une épaisseur Æt, est représenté par un ou plusieurs nuages de grains sur le plan FG. Cet instant constitue la définition d’une trame; et la réunion de plusieurs de ces trames dans un ordre donné, décrit ou prescrit la vie de ce complexe sonore (Xenakis, 1971).
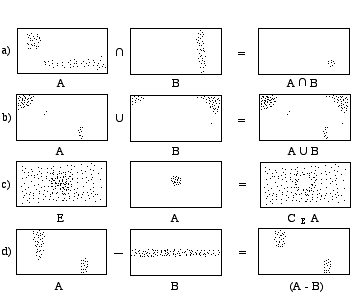
Xenakis va utiliser différentes équations d’algèbre pour combiner les trames, et pouvoir ainsi déduire de nouvelles trames pour la construction des processus sonores. Il utilise les opérations élémentaires suivantes: intersection des deux trames, réunion de deux trames, complémentaire d’une trame A par rapport à une trame E, différence entre une trame A et une trame B (Figure 1). Il définit ensuite trois facteurs de base qui vont déterminer la construction théorique d’un processus sonore et son efficacité sensorielle: la densité des événements élémentaires; la situation géographique des événements sur les trames; et l’ordre ou le désordre des événements. Selon Xenakis, la densité et la topologie des grains sont plutôt des incarnations palpables simplifiées de la notion du désordre; en partant de ce désordre on peut trouver des directions possibles d’ordre, mais on pourrait aussi effectuer des processus où l’ordre devient désordre.

Figure 1.- Opérations élémentaires avec les trames. a) intersection de deux trames. b) réunion de deux trames. c) complémentaire d’une trame A par rapport à une trame E. d) différence entre deux trames (Xenakis, 1971).
L’estimation quantitative d’ordre ou de désordre de l’évolution d’un complexe sonore peut être établie par l’introduction de la notion de probabilité. Xenakis appelle entropie d’un groupe d’éléments la quantité d’ordre ou de désordre définissable dans ce groupe. Selon Xenakis, notre oreille est sensible aux différents degrés d’entropie existante dans les phénomènes sonores, et il part de ce fait pour établir une esthétique où l’on va effectuer différents types de transitions entre états sonores d’ordre et de désordre (et vice-versa). On peut alors imaginer un état sonore premier avec une entropie générale moyenne donnée, puis, on peut lui faire subir une transformation. Cette transformation peut avoir trois effets: le degré de complexité (la variété) n’a pas changé, la transformation est neutre et l’entropie globale n’a pas varié; le degré de complexité a augmenté, l’entropie aussi; la transformation était simplificatrice, l’entropie a diminué. Ces effets vont affecter le maintien ou la transition entre différents états d’ordre et désordre possibles Ces états sont les suivants: désordre parfait (•), désordre partiel (n ou m), ordre partiel (n ou m), ordre parfait (0).
Les trames peuvent être classées suivant le critère de l’ataxie à l’aide de deux paramètres de désordre: la variété de fréquences et la variété des intensités. Ainsi, une trame est formulée par un couple des valeurs de l’entropie attribué aux fréquences et aux intensités des grains. Il est possible de construire un tableau entropique de trames (Figure 2). Xenakis donne des exemples pour la construction des trames. Ainsi, pour créer une trame avec désordre parfait des fréquences et des intensités (•,•), on pourrait utiliser la formule du Poisson:
![]()
En utilisant cette formule, la distribution des grains va varier selon leur densité dans chaque trame; avec une basse densité il y aura une modification perceptible, mais avec une haute densité, il n’y aura presque pas de différence auditive entre chaque trame, car on aura simplement différentes nuances de son blanc. La formule de Poisson aide seulement à construire des trames d’un désordre parfait et homogène; toutefois, on peut construire toutes les trames du tableau entropique si on applique les différentes opérations élémentaires sur seulement quelques trames réalisées avec cette formule.
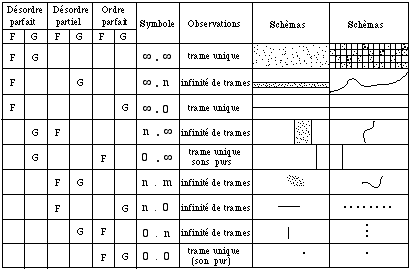
Figure 2.- Tableau entropique des trames.
Xenakis présente ensuite une méthode pour enchaîner les trames créés par les opérations élémentaires. Il faut simplement représenter chaque trame avec un symbole spécifique (un terme) et ensuite créer une succession de trames en effectuant plusieurs types de transitions entre les différents termes. Un groupe de transitions constitue une transformation donnée. Xenakis va proposer différents types de transformations entre les groupes de transitions. Ces transformations peuvent être closes, (lorsque le groupe des transformés ne contient que des éléments appartenant au groupe des termes)univoques (lorsque chaque terme a un seul transformé, non univoques, biunivoques (lorsque chaque terme a un seul transformé et lorsque chaque transformé est issu d’un seul terme).
Le pas suivant est la réalisation des représentations matricielles des transformations, et puis celle des opérations entre les différentes matrices (Figure 3). Une transformation peut aussi être définie comme un mécanisme. Ce mécanisme est déterminé lorsque la transformation correspondante est univoque et close, et il est non déterminé lorsque la transformation correspondante n’est pas univoque. Dans ce dernier cas, la transformation est dite stochastique. Selon Xenakis, toutes le règles des différents styles musicaux constituent des mécanismes. Le compositeur d’avant-garde, ne se contentant pas d’utiliser des mécanismes anciens, en proposera alors de nouveaux. Dans la musique algorithmique par exemple, une chaîne de Markov est un mécanisme qui constitue une suite stochastique. Les probabilités de transition entre deux termes d’une chaîne de Markov (A et B) pourraient être représentées par une matrice de probabilités de transition (Figure 4). On peut aussi créer des matrices de probabilités à la main: par exemple, une matrice d’entropie maximale serait constituée d’un 50% de possibilités de transition entre les différentes permutations de ces deux termes (AA, AB, BA, et BB), et une matrice d’entropie minimale serait constituée de 100% ou de 0% de probabilités entre les différentes permutations (Figure 5a et 5b). Si une matrice de probabilités de transition a un état théorique d’équilibre, alors elle tend vers une stabilité et une homogénéité ergodique dans le temps.
Finalement, pour achever sa théorie, Xenakis arrive à la conclusion suivante: "Le critère fondamental de l’évolution d’une musique peut être formé par les transformations de l’ataxie dans le temps... On peut soit introduire peu à peu les richesses d’une musique ou par contre donner d’un coup tout la variété et puis la monnayer dans le temps" (Xenakis, 1971). Les évolutions élémentaires de l’ataxie sont montrées dans la figure 6.
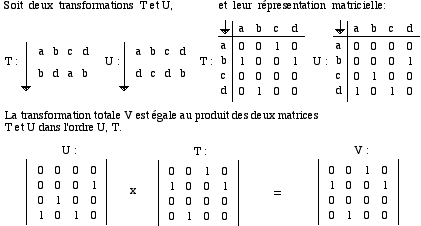
Figure 3.- Deux transformations des termes; leur représentation matricielle; et une opération effectuée entre les deux matrices donnant comme résultat une nouvelle matrice (Xenakis, 1971).

Figure 4.- Chaîne de Markov de 50 transitions entre deux trames (A et B).
a) Matrice des fréquences de transitions réelles. b) Matrice des probabilités
(fréquences relatives) des transitions (Xenakis, 1971).

Figure 5.- a) Matrice d’entropie maximale. b) Matrice d’entropie minimale
(Xenakis, 1971).
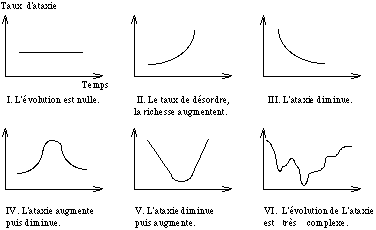
Figure 6.- Les évolutions élémentaires de l’ataxie. Dans le diagramme VI, l’évolution de l’ataxie est très complexe mais elle peut s’analyser par les trois premiers diagrammes. (Xenakis, 1971).
Alors, tout discours sonore n’est qu’une perpétuelle fluctuation de l’entropie sous tous ses formes. Dans la musique dodécaphonique par exemple, une fois qu’on entend les douze tons, l’imprévisibilité tombe à zéro, et l’entropie aussi. A ce moment-là, l’entropie (la richesse) apparaît dans d’autres domaines comme le timbre, l‘harmonie, les durées de notes, etc.
Malgré la logique de son système d’ataxie, Xenakis est conscient que les lois de la perception auditive ne sont pas en rapport direct avec le degré d’entropie. Il y a par exemple des musiques répétitives incantatoires qui cherchent un effet de tension maximale avec une entropie minimale. On pourrait aussi avoir deux musiques avec deux entropies différentes, et les percevoir cependant comme identiques. Toutefois, ceci n’empêche pas qu’il soit possible de composer de la musique en utilisant des carnets de trames; d’autre part, Xenakis avoue que seulement l’expérimentation et la recherche peuvent nous conduire à mieux maîtriser le rapport entre ce système d’ataxie et notre perception.
Pour conclure, Xenakis redéfinit les trois critères fondamentaux pour la construction de trames:
1) Un critère topologique, fondamental pour pouvoir déduire la distribution des grains dans la trame en utilisant la notion d’entropie.
2) Un critère de densité, qui constitue une qualité immédiatement perceptible. On utilise aussi la notion d’entropie pour en définir le taux de densité.
3) Un critère d’ataxie pure défini par rapport aux grains d’une trame, où l’on a trois paramètres: la fréquence moyenne, l’amplitude moyenne, et la densité moyenne des grains. Ici, pour la création d’une trame on peut établir trois protocoles indépendants ou liés, puis trois matrices de probabilités de transition couplées ou non. Chacune des matrices aura son entropie et les trois matrices couplées auront une entropie moyenne.
2.- Critique du système de Xenakis.
Le système granulaire par trames de Xenakis est sans doute très complexe. Sa grande vertu est la diversité de possibilités (du point de vue mathématique) pour créer des transitions fines entre les différentes trames. L’idée d’utiliser un petit nombre de trames pour en créer d’autres est économique, musicale, et pratique pour le calcul si l’on envisage la création d’une application pour l’ordinateur. De plus, si on compare ce système avec les méthodes postérieures qui utilisent des tendency masks (et qui sont beaucoup plus simples), le système de Xenakis semble être plus efficace pour la modification brusque et soudaine des paramètres des grains dans le temps. La densité des grains dans un système qui utilise des tendency masks est en rapport avec des concepts tels que: choix des délais entre les grains, choix statistique de la durée de grains, et limites de la mémoire et du DSP de l’ordinateur pour la densité maximale. Puis, ces systèmes ont une tendance naturelle à effectuer des modifications continues des paramètres pour créer des macro-processus qui varient très lentement dans le temps. Par contre, la méthode de Xenakis est plus discrète du point de vue de ces macro-processus, car chaque état global des grains peut changer radicalement à chaque micro-instant dans le temps. Il me semble qu’avec cette perspective, la structure d’un son ou d’un ‘complexe sonore’ tendent à varier plus richement dans le temps. L’optique de Xenakis se concentre tout de suite sur l’aspect spatial des grains (du point de vue de la fréquence, de la densité et de l’amplitude des grains), tandis qu’avec les autres méthodes, on est incliné à penser à chaque paramètre séparément, et on obtient un résultat qui pourrait devenir esclave de la simplification du système.
La sophistication du système de Xenakis peut donner des sons riches et intéressants et même des compositions entières dans le niveau de la macro-forme. Néanmoins, sa limitation principale est qu’il est modélisé pour composer avec une esthétique stochastique, même en ayant la possibilité de représenter théoriquement différents styles musicaux (anciens et nouveaux). Cette caractéristique fait que le contrôle des grains sur le niveau spectrale est difficile, particulièrement si l’on veut être sûr de ce qui va arriver. Je pense que pour avoir un contrôle du timbre dans le micro-domaine, il faut utiliser des méthodes plutôt déterministes qui nos donnent une certitude sur le résultat. Bien entendu, on pourrait ensuite les enchaîner avec d’autres méthodes qui possèdent un certain degré d’indéterminisme pour chercher des effets sonores différents, mais pour avoir un son bien défini dans le domaine spectral, il faudra trouver des moyens en rapport avec l’analyse du signal. Un autre défaut du système granulaire par trames de Xenakis est qu’il n’envisage pas le contrôle de la durée des grains, et pour cette raison, on ne peut pas effectuer des transitions sonores entre le micro-temps et le macro-temps; c’est le désavantage d’avoir une vision discrète de type global (qui privilégie la macro-structure) par opposition à une vision où l’on pense d’abord aux caractéristiques individuelles des grains. D’autre part, Xenakis ne se soucie pas sur l’utilisation de différentes enveloppes, et d’ailleurs, l’enveloppe rectangulaire qu’il propose génère des artefacts. Il est dommage qu’il n’ait pas eu les moyens à l’époque pour mettre en pratique son système sur un ordinateur, pour vérifier ainsi l’aspect théorique et réaliser des modifications en partant de l’expérience.
Malgré quelques limitations, il y a certains aspects de la méthode de Xenakis qui demeurent fort intéressants, comme c’est le cas de la dichotomie ordre-désordre, qui nous permet surtout de créer des sons proches aux phénomènes naturels. Je suis certain que s’il existait une application pour ordinateur, on pourrait en profiter. Par exemple, il serait possible d’effectuer une interpolation entre deux trames avec différents degrés d’entropie, par le moyen d’un algorithme qui cherche les états intermédiaires pour créer une série de transitions entre elles (ce processus est appelé morphing). Enfin, avec le développement des nouveaux algorithmes, on pourrait enrichir le système de Xenakis en conservant son essence, et ceci donnerait des sons granulaires intéressants et très particuliers.
3.- Quelques algorithmes stochastiques et leur possible utilisation dans la synthèse granulaire.
a) Distributions aléatoires.
Une opération aléatoire qui privilégie toutes les valeurs avec le même pourcentage de probabilités n’est pas stochastique. Dans le chapitre sur la synthèse granulaire formantique, j’ai décrit le logiciel GiST développé à l’IRCAM (Eckel et Rocha Iturbide, 1995). On a utilisé le programme MAX (Puckette, 1991), avec lequel on peut utiliser une table de distribution aléatoire où l’on peut sélectionner différents poids pour chaque valeur afin d’obtenir une distribution aléatoire hétérogène (voir figure 12b du quatrième chapitre). Richard Moore (1990) appelle ces systèmes Biased Choices (choix biaisés) car certains choix sont plus probables que d’autres dans une portée spécifique de valeurs possibles; ces systèmes peuvent être définis comme stochastiques. Un algorithme stochastique simple en musique pourrait être le suivant: choix d’un nombre au hasard entre 1 et 4 où les valeurs 1,2,3 représentent la note Do, et où la valeur 4 représente la note Ré. Avec cet algorithme la note Do a 75% de probabilités d’être choisie, tandis que la note Ré en a seulement 25%.
Il y a plusieurs algorithmes pour la génération de variables aléatoires qui donnent des distributions différentes. Ces algorithmes constituent des fonctions mathématiques. Voici quelques-unes: distribution linéaire, distribution triangulaire, distribution Exponentielle, distribution de Gauss, distribution de Cauchy, distribution Arcsinus, distribution Gamma, distribution de Poisson, etc. L’avantage de ces distributions est qu’avec une simple équation on peut générer une suite riche de valeurs, tandis qu’avec une table, il faut dessiner les différents poids à la main.
On pourrait utiliser plusieurs équations de distribution aléatoire pour contrôler la synthèse granulaire, par exemple, la distribution de Poisson pour contrôler les fréquences des grains, la distribution rectangulaire pour contrôler les délais entre les grains, et la distribution exponentielle pour contrôler les amplitudes. Le problème est qu’en termes globaux le résultat de chaque paramètre serait trop uniforme; toutefois, on pourrait soit changer les valeurs des fonctions mathématiques dans le temps, soit changer de fonction au cours du temps, ou même interpoler les valeurs des différentes fonctions dans le temps. Ces équations ont été très utilisées sur le niveau macro, pour générer des fréquences de notes, des temps d’attaques, etc, mais le problème est toujours celui de l’uniformité globale du résultat, à moins qu’on effectue les opérations dynamiques que je vient de décrire.
b) Promenades aléatoires.
La promenade aléatoire est un modèle stochastique plus directionnel car chaque valeur générée dépend uniquement de la valeur antérieure selon l’équation: h(tn) = h(tn-1) + X
où h(tn) est la valeur du modèle à l’instant tn; h(tn-1) est la valeur du modèle à l’instant tn-1; et X est une variable aléatoire quelconque indépendante des valeurs de h(t).
La valeur X peut suivre plusieurs distributions: uniforme dans {1,0, +1} (promenade aléatoire simple); et Gauss avec moyenne = 0 (mouvement Brownien).
Dans le logiciel GiST pour la synthèse granulaire formantique (Eckel et Rocha Iturbide, 1995) on a appliqué un facteur brownien pour affecter les tendency masks qui engendrent des valeurs aléatoires entre deux limites spécifiques. Ici une valeur brownienne équivalente à 0 signifie que l’équation marche à 100%. Imaginons qu’on a un tendency mask pour contrôler la transposition des grains avec les valeurs -1 (demi-tons) et +24 (demi-tons) et un facteur brownien de 0. Les valeurs de transposition vont être engendrées à partir de la première valeur Random, si cette valeur est 0, le facteur brownien cherche une valeur aléatoire proche de 0, soit plus haut que 0 ou au-dessous de 0 mais jusqu’à -1, puis il cherche une autre valeur proche de la valeur choisie, et ainsi de suite. On va alors monter et descendre de façon plutôt continue par petits bonds. Si on augmente le facteur brownien (la portée de ce facteur est de 0 à 1) à 0.3, on aura alors des bonds toujours plutôt continus mais beaucoup plus grands car la portée a été augmentée. Finalement, avec un facteur égal à 1, on n’a plus de facteur brownien, mais une distribution aléatoire homogène.
Le mouvement Brownien a été très efficace dans notre application de synthèse granulaire pour la transposition micro-tonale et pour la spatialisation des grains. Ces deux paramètres peuvent beaucoup altérer un son granulaire. Donc, en utilisant cet algorithme, on a réussi à avoir un effet micro-tonal qui varie subtilement, et un parcours spatial des grains clair et perceptible.
c) Distribution 1/f.
Le spectre à longue terme des signaux musicaux tend à avoir un spectre d’énergie qui diminue en fréquence tel que 1/f (Moore, 1990). Voss et Clarke (Voss., Clarke, 1978) ont analysé des échantillons de différents styles musicaux et ils ont trouvé que la distribution de la fréquence et du loudness (amplitude en dB) était proche de la distribution 1/f. Si la densité spectrale varie en fréquence par la distribution 1/f2 , on a alors du mouvement brownien. Avec le mouvement brownien on a seulement des corrélations à court terme, tandis qu’à long terme il n’y a pas de sens ou de direction. Par contre, avec la distribution 1/f on a une corrélation courte qui est plus large que la corrélation à long terme, mais la corrélation à long terme n’est pas égale à zéro (Risset, 1989). La distribution 1/f a donc un indice de mémoire plus grand que le mouvement brownien.
La distribution 1/f a la caractéristique d’auto-similarité, et ses valeurs ont par conséquence un comportement fractal. Cette formule garde un bon équilibre entre surprise (Random total = 1/1) et redondance (le mouvement brownien 1/f2). On peut associer facilement cette distribution à des paramètres musicaux, car la structure du langage musical est hiérarchique (une structure proche de la structure fractal). Même si cette distribution est plus organique et plus proche des phénomènes de la nature, son comportement global est homogène, et elle n’a pas de direction définie. Toutefois, elle présente une structure intéressante de mouvements continus qui bondissent de temps en temps à des états discontinus, et ceci pourrait être utilisé par exemple pour contrôler les délais des grains, ainsi que les fréquences des grains dans un champ micro-tonal. Une autre utilisation possible de cette distribution serait de faire varier la valeur de la puissance de f (b) entre 0 et 2 (soit 1/f b où la valeur de b est entre 0 et 2). De cette manière, on pourrait avoir des transitions entre des valeurs aléatoires totales, la distribution 1/f, et du mouvement brownien (1/f2).
d) Les Chaînes de Markov.
Une chaîne de Markov est un algorithme stochastique beaucoup plus sophistiqué que les systèmes Biased et plus proche des promenades aléatoires (mais beaucoup plus complexe). On a vu dans ce chapitre comment Xenakis a décrit la possible utilisation de cet algorithme pour une succession de trames. Cependant, il n’a pas expliqué le mécanisme de fonctionnement de l’algorithme.
Par opposition aux systèmes Biased, où l’ordre des résultats est indifférent pour la structure, les chaînes de Markov sont des modèles stochastiques avec corrélation temporelle, c’est-à-dire, avec une mémoire. Les promenades aléatoires appartient à ce groupe de modèles, mais elles sont beaucoup moins spécifiques. Expliquons brièvement ce qu’est une chaîne de Markov et comment on pourrait appliquer cet algorithme à la synthèse granulaire (mise à part l’utilisation que Xenakis a fait d’elle).
Soit un ensemble d’états: a=(a1, a2, ...,ak) et le vecteur de probabilités de passage associé à l’état Pk: Pk = (Pk1, Pk2,...,Pkn) où Pkn est la probabilité de passage de l’état k à l’état n. X est une suite de réalisations, où chaque Xt représente un des états ak au moment t= 0, 1, 2, .... On dit que la suite ordonnée constitue une chaîne de Markov simple si Xt dépend exclusivement de Xt-1.
Par exemple, soit l’ensemble d’états des différents délais entre les grains:
P10 msecs = (.35, .25, .15, .05, .20)
P20 msecs = (.25, .35, .15, .00, .25)
P40 msecs = (.35, .20, .10, .05, .30)
P80 msecs = (.40, .30, .10, .00, .20)
P160 msecs = (.40, .20, .00, .10, .30)
On peut représenter ce processus par une graphie des transitions:
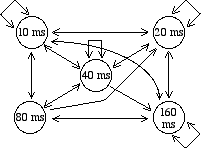
On peut aussi le représenter avec une matrice, où chaque case indique la probabilité de transition de l’état ‘horizontale’ en vers la colonne:
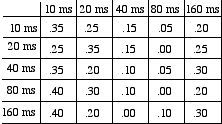
Si on a par exemple une valeur de délai de 10 msecs, la valeur suivant la plus probable sera le même délai de 10 msecs avec .35, soit le 35% de probabilités, et la deuxième valeur la plus probable sera de 20 msecs avec le 25% de probabilités. Par contre, si on a une valeur de 160 msecs, la valeur suivante la plus probable sera de 10 msecs avec 40% de probabilités et la deuxième valeur la plus probable sera 160 msecs avec 30% des probabilités.
En faisant cette matrice j’ai essayé de créer un processus stochastique qui effectue des modulations un peu radicales entre le micro-temps et le macro-temps. Imaginons des grains d’une durée de 50 msecs. Les valeurs de délai les plus privilégiées sont 10 msecs et ensuite 20 et 160 msecs, ce qui veut dire qu’on aura surtout des déclenchements de grains dans le micro-temps avec les valeurs 10 et 20 msecs (à peu près le 3/5 du temps), et qu’un peu plus de 1/5 du temps il y aura des bonds discontinus vers la valeur de 160 msecs. Les valeurs de 40 et de 30 msecs auront à eux deux moins de 1/5. Donc, ce processus en termes réels va engendrer un son riche du point de vue spectral, car on aura des effets de flanging à cause des micro-délais (10 et 20 msecs), mais de temps en temps on aura des grains isolés à cause de la valeur de 160 msecs. On pourrait effectuer une autre chaîne de Markov pour les amplitudes des grains, couplé à celle-ci, de telle façon que s’il y a des valeurs de 160 msecs, on ait une amplitude plus grande, pour accentuer les grains isolés.
Je peux facilement imaginer l’utilisation de plusieurs matrices de valeurs pour un seul paramètre de telle manière que les préférences de valeurs puissent changer dans le temps. Il faudrait donc fabriquer quelques matrices à l’avance, et créer un algorithme pour effectuer des interpolations entre elles.
Nous venons de voir comment construire une chaîne de Markov de premier ordre, mais on peut aussi avoir des chaînes de deuxième, de troisième ordre ou plus. Une chaîne de deuxième ordre par exemple, garde en mémoire les deux dernières valeurs précédentes, une chaîne de troisième ordre garde les trois dernières valeurs, et ainsi de suite. Donc, avec une chaîne de deuxième ordre on peut spécifier davantage le parcours stochastique voulu, et avec une chaîne de troisième ordre, davantage encore. Pour conclure, il est facile de percevoir qu’on peut modéliser plusieurs processus musicaux avec des chaînes de Markov, car elles ont de la mémoire, elles peuvent engendrer de chemins préférentiels (chemins de moindre entropie ou de probabilité maximale), elles ont la possibilité d’associer les probabilités de transitions à des potentiels d’attraction, et on peut les associer à des graphes de transitions (Malt, 1992).
4.- Critique aux tendency masks.
Au cours de ce travail on a analysé plusieurs approches de l’utilisation des tendency masks. On ne reviendra pas en détail sur les concepts de base; pour cela il vaudra mieux revenir aux deux premiers chapitres, qui comportent une étude étendue sur le sujet. Aussi, dans le quatrième chapitre, j’ai décrit le système de synthèse granulaire formantique GiST (Eckel et Rocha Iturbide, 1995) où j’ai utilisé des tendency masks en combinaison avec d’autres algorithmes.
Dans cette section je voudrais faire une critique aux tendency masks pour savoir s’il est possible de développer davantage cette méthode, faire des améliorations, l’hybrider, ou s’il vaudrait mieux changer d’optique et chercher d’autres moyens de contrôle.
L’idée fondamentale des tendency masks est d’utiliser un algorithme pour générer des valeurs, mais tout en ayant certaines contraintes ou limites. On peut donner ainsi une direction globale précise au processus sonore. Normalement on utilise un tendency mask au moyen d’une table avec deux axes où l’on dessine le trajet de la tendance des valeurs en spécifiant une valeur maximale (au-dessus de la fonction) et une valeur minimale (au-dessous de la fonction). Ces valeurs sont fixes. Toutefois, on peut utiliser un tendency mask avec deux séries de valeurs indépendantes (deux enveloppes différentes), une pour les valeurs maximales et l’autre pour les valeurs minimales, ayant ainsi une variation des bornes dans le temps. J’ai trouvé cette deuxième approche plus riche en possibilités, et pour cette raison je l’ai utilisée dans les deux applications que j’ai réalisé (Rocha Iturbide, 1994, 1995). Il y a une troisième possibilité que je n’ai pas envisagé et qui a été utilisée par Mara Helmuth pour l’application Stochgran (Helmuth, 1991, 1995). Elle s’est servi d’un tendency mask avec deux enveloppes pour les bornes inférieure et supérieure, mais aussi d’une courbe, à laquelle elle a donné un facteur de "tightness" (étroitesse) qui donne un certain poids autour d’elle (Helmuth, 1991). Dans une application postérieure elle a aussi appliqué le facteur de "tightness" aux deux enveloppes (Helmuth, 1995).
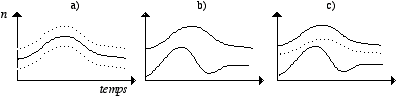
Figure 7.- Trois types différents de tendency masks. a) tendency mask simple, avec deux bornes (ou enveloppes) des valeurs maximales et minimales fixes. b) tendency mask avec deux enveloppes indépendantes, une pour la borne maximale et l’autre pour la borne minimale. c) tendency mask avec deux enveloppes indépendantes (bornes maximale et minimale) et une courbe (ligne pointillée) qu’indique un effet de "tightness" autour d’elle.
a) Avantages et désavantages.
Le concept fondamental de tendency mask est stochastique. Ce concept est très pratique pour le compositeur car il peut dessiner une trajectoire visuelle, ne dépendant guère de la sophistication d’un algorithme stochastique qui en général n’a pas assez de directionalité et qui est parfois trop imprévisible. De plus, on peut utiliser différents algorithmes pour générer des valeurs aléatoires, ce qui donne différentes nuances au mouvement interne des grains dans un nuage granulaire. Or, les tendency masks servent pour générer des macro-processus, c’est-à-dire, des sons ou des complexes sonores où ce qui intéresse est le résultat global. D’ailleurs, toutes les opérations stochastiques partagent cette même vision, et leur problème fondamental est qu’un contrôle plus spécifique des grains est impossible, en particulier si l’on veut contrôler le spectre du son dans le micro-temps, ou contrôler harmoniquement un complexe sonore dans le macro-temps. Pour cela, il faudra hybrider les processus stochastiques avec des processus déterministes de manière à avoir un équilibre entre les deux, ou réaliser des transitions possibles entre les deux domaines. Je développerai cette idée dans la section sur le contrôle hybride.
Malgré leurs défauts, les tendency masks sont très pratiques pour la composition stochastique des macro-structures sonores, surtout grâce à la spécificité directionnelle qu’on peut donner. Cependant, dans certains cas peut-être, il vaudrait mieux abandonner ce type de contrôle qui est un peu déterministe (en termes généraux), et découvrir les résultats d’autres algorithmes stochastiques de direction un peu moins précises, mais peut-être un peu plus riches et complexes au niveau local. Nous avons vu dans ce chapitre qu’il y a une grande variété des fonctions de distribution aléatoire, or on n’a pas encore utilisé la plupart d’elles pour des applications de synthèse granulaire. On pourrait peut-être combiner ces algorithmes avec l’utilisation d’un tendency mask avec deux enveloppes qui fonctionneraient comme une bande de filtrage (un passband dynamique) qui accepterait seulement les valeurs générées qui se trouvent dans les deux bornes.
b) Le contrôle des tendency masks en temps réel.
Les tendency masks s’adaptent bien au contrôle de la synthèse pour effectuer des processus où on détermine tous les paramètres à l’avance, mais si l’on veut modifier les paramètres au cours de la synthèse il faut développer des interfaces appropriées. Avec le logiciel GiST (Eckel et Rocha Iturbide, 1995) on a la possibilité d’affecter en temps réel la vitesse et la direction de lecture des différents tendency masks. Il y a un patcher nommé dynamic control (Contrôle dynamique) qui est branché au patch où l’on détermine les tendency masks. Avec le Contrôle Dynamique on peut contrôler à la main chaque tendency mask qui correspond à chacun des paramètres de la synthèse granulaire formantique. Le problème est que chaque tendency mask a un contrôleur séparé (un slider), et que pour contrôler tous les paramètres à la fois, il nous faut une interface plus sophistiquée que la souris. Même avec les touches du clavier, il nous serait difficile de contrôler en même temps huit paramètres, et surtout en ayant besoin de deux touches du clavier pour chaque paramètre (seize touches!). Alors, seulement avec un midi fader ou avec un interface spécifiquement construit pour ce but on pourrait avoir un contrôle dynamique de tous les paramètres en même temps. Une autre option serait de contrôler plusieurs paramètres d’un même geste. Selon Todoroff, ce procédé facilite le contrôle de la synthèse pour les compositeurs qui sont dans le noir quand il y a trop de paramètres (Todoroff, 1995). Todoroff utilise la technique d’interpolation dynamique entre différentes séries de paramètres, où l’on peut effectuer des transitions en utilisant soit la souris, soit un gant de données. Les premiers systèmes de synthèse en temps réel comme le SYTER ont utilisé cette méthode avec des boules graphiques, chaque boule représentant une série de paramètres de synthèse différente. Le résultat est très différent par rapport à la synthèse automatisée, car notre geste est comparable au geste d’un instrumentiste.
Pour conclure, l’idée d’utiliser un seul geste pour contrôler plusieurs paramètres est intéressante et efficace pour le temps réel, mais pas forcément meilleure que l’automatisation des paramètres. Tout dépend de ce qu’on veut faire, de notre choix esthétique. Pour la composition, il vaudra mieux avoir toujours un contrôle spécifique pour chaque paramètre. Si on ne peut pas jouer un orchestre, ceci ne veut pas dire qu’il faut jouer du piano. Toutefois, le développement d’idées dans le domaine du temps réel fait que chaque fois on est plus près de maîtriser des instruments plus complexes, et le geste donnera toujours à la synthèse une nuance musicale particulière à ne pas dédaigner.
III- Contrôle Chaotique.
Au début de ce chapitre nous avons fait un bref parcours historique sur le développement des algorithmes musicaux. Nous avons vu comment l’apparition de la science du chaos, ainsi que d’autres lois qui expliquent des phénomènes naturels, ont apporté une nouvelle manière de regarder ce qui nous entoure. Les lois newtoniennes de cause-effet et la logique cartésienne ont alors ouvert la voie aux théories dynamiques non-linéaires. La vision d’un déterminisme total a disparu, car un facteur d’indéterminisme est entré en jeu dans de nombreux phénomènes qui auparavant étaient théoriquement prévisibles à 100%.
Les phénomènes dynamiques non linéaires constituent des processus complexes qui ont (comme les lois stochastiques) une directionalité plus ou moins déterminée dans un niveau global, mais au niveau local ils ont des zones complètement imprévisibles. On a vu que l’avantage des équations de la théorie du chaos par rapport à beaucoup de processus stochastiques, est qu’elles génèrent des évolutions de valeurs complexes, et que la modification initiale des données produit une infinité d’évolutions possibles (Bidlak, 1992). Donc, elles sont très économiques. On a vu également que d’autres aspects de la théorie du chaos tels que le principe d’auto-similarité et les espaces fractals ont intéressé beaucoup de compositeurs car ils sont très proches des structures musicales (Risset, 1989).
L’utilisation des algorithmes chaotiques a été appliquée sur le macro-domaine musical en particulier, c’est-à-dire, pour les paramètres des notes (rythme et fréquence) dans les différentes gammes musicales possibles. Toutefois, depuis la fin des années quatre-vingt, on a commencé à utiliser ces algorithmes pour le contrôle de la synthèse sonore. J’ai étudié dans le deuxième chapitre l’application des équations de chaos sur le système de Barry Truax (1990), et j’ai aussi parlé de l’application d’une équation de chaos pour le logiciel GiST (Eckel et Rocha Iturbide, 1995). Nous allons analyser maintenant certaines de ces équations en détail, ainsi que d’autres équations de chaos qui n’ont pas été forcement utilisées auparavant, pour pouvoir alors analyser différentes possibilités d’application à la synthèse granulaire. Avant de commencer, j’établirai une classification des systèmes chaotiques pour voir les caractéristiques essentielles des différents groupes.
Les systèmes chaotiques peuvent être classifiés en deux groupes essentiels, celui de dissipation et celui de conservation. Les systèmes de dissipation correspondent aux phénomènes dont la friction joue un rôle important et où l’énergie est dissipée dans l’environnement, tandis que les systèmes de conservation peuvent être représentés par la dynamique des corps célestes, où l’énergie est conservée. Les systèmes de dissipation ont une perte d’énergie dans le temps, c’est-à-dire, qu’il y a un rétrécissement de leur aire d’action (phase space) qui donne lieu à la formation d’un attracteur; une fois qu’il se sont stabilisés sur leur attracteur, ils maintiennent un comportement relativement constant. D’autre part, les systèmes de conservation gardent une phase constante ne donnant pas lieu à des attracteurs, mais produisant des orbites qui restent dans un point spécifique, ou qui effectuent des cycles parmi une série limitée de points, ou qui errent à travers leur espace de phase (phase space). Ces systèmes ont beaucoup moins de consistance interne et sont marqués par des changements de texture drastiques dans leur portée de valeurs (Badlick, 1992).
Les systèmes chaotiques sont formulés soit par cartes itératives (dans une ou deux dimensions), soit par des écoulements continus (dans trois ou plusieurs dimensions). Mais la théorie du chaos est tellement large, qu’on ne peut pas effectuer une classification aussi étroite. Par exemple, la géométrie fractale et le principe d’auto-similarité ne coïncident pas forcément avec la définition des systèmes de dissipation et de conservation. La seule chose certaine est que les différents aspects de la théorie du chaos coïncident dans le concept fondamental de non-linéarité.
1.- Cartes non-linéaires itératives à deux dimensions.
Les cartes non-linéaires à deux dimensions ont été utilisées en musique, surtout dans le macro-domaine. Pressing (1988) et Badlick (1992) les ont utilisées pour cartographier les valeurs en fréquence des notes successives, mais d’autres compositeurs les ont utilisées aussi pour générer différents types d’événements musicaux dans la macro-échelle (Di Scipio, 1990., Gogins, 1991). Dans le micro-domaine (c’est à dire, pour la synthèse), Truax a été l’un des pionniers (1990). Il a effectué différentes applications pour la synthèse granulaire en temps réel avec son système basé sur un DSP DMX-1000 qui est contrôlé par un PDP Micro 11 (Truax, 1988).
Il est curieux que le premier paramètre musical choisi pour l’exploration des systèmes chaotiques à deux dimensions - autant pour les événements au niveau macro que pour la synthèse - soit celui de la fréquence. Les domaines temporels du rythme et du micro-rythme (dans la synthèse), ont été beaucoup moins explorés. Or, la fréquence est un paramètre qui décrit clairement les différentes structures du chaos, mais nous avons comme résultat des motifs mélodiques accentués qui ne sont pas forcément musicaux. Avec la synthèse granulaire on a le même problème, sauf si on travaille sur des portées de fréquence micro-tonales.
La façon d’associer les paramètres des différentes équations du chaos avec les paramètres musicaux est un problème capital. Selon Truax: "D’un point de vue esthétique ou philosophique, il n’est pas clair que l’attribution des paramètres (mapping) à partir de fonctions non-linéaires soit plus musicale en soi que, par exemple, l’attribution des paramètres à partir des fonctions stochastiques. La musicalité repose sur la connaissance musicale de celui qui réalise l’attribution plutôt que dans la fonction choisie" (Truax, 1990). On verra au long de cette section différentes démarches par rapport à l’attribution des paramètres, et j’offrirai ma vision personelle.
a) L’équation logistique différentielle.
Dans le quatrième chapitre, on a analysé en détail une application de l’équation logistique différentielle réalisée avec le logiciel GiST (Eckel et Rocha Iturbide, 1995). Cette équation: xnext = rx (1 - x) décrit la croissance d’une population par itérations successives. Ses paramètres sont: r = taux de croissance de la population qui varie entre 0 et 3.9, x = la valeur initiale pour la population, et xnext = le résultat, qui devient x dans la prochaine itération. Cette équation a été explorée par May (1976), qui a découvert certaines propriétés chaotiques. Il a constaté que l’équation donnait différentes évolutions de valeurs conditionnées par la valeur du taux de croissance. Si r £ 1 , les valeurs convergent sur zéro; si r > 1 et r < 3, les valeurs convergent rapidement sur une valeur non égale à zéro; autour de r = 3 , les valeurs font une bifurcation en 2, 4, 8 et 16 cycles; finalement si r > 3.57 , on a le chaos. Le chaos dans ce cas n’est pas un désordre total, car dans cette zone (entre 3.57 et 3.9) il y a une alternance entre des valeurs non périodiques aléatoires et des valeurs périodiques, et donc, on a une certaine structure sur le niveau globale (Figure 8).
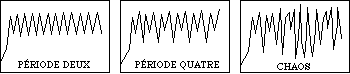
Figure 8.- Doublage de périodes et chaos dans l’équation logistique différentielle (Gleick, 1987).
On peut voir comment l’équation logistique donne des évolutions de valeurs intéressantes. Ces valeurs peuvent être facilement associées à la synthèse en général; Barry Truax en donne l’exemple avec le contrôle du taux de changement de la phase d’un simple oscillateur. Avec r entre 1 et 3, il y aura un comportement transitoire jusqu’à ce que l’oscillation se stabilise dans une fréquence fixe; avec r > 3.0, il y aura des doublements de périodes qui donneront un signal modulé en fréquence, et dans la région du chaos on aura des périodicités complexes. Mais cet exemple est un peu pauvre selon lui, et il propose alors l’utilisation de cette équation pour contrôler la fréquence des grains dans la synthèse granulaire (Truax, 1990).
Mon expérience personelle avec l’utilisation du logiciel GSKX de Truax pour le contrôle chaotique de la fréquence des grains m’a amené à conclure que l’évolution des fréquences est trop structurée et prévisible, et que l’on a toujours la même structure globale. Comme je l’ai dit auparavant, si on travaille à un niveau micro-tonal, on peut se soustraire de la perception de cette structure, et avoir des résultats sonores très intéressants au niveau du timbre et qui varient avec le changement du r, mais dès que l’on commence à entendre des intervalles, le résultat sera toujours le même du point de vue de la forme. Toutefois, on pourrait utiliser des déclenchements de grains synchrones et effectuer une synthèse granulaire formantique. Dans ce cas, si on établit bien les paramètres, on peut créer des sons intéressants avec plusieurs régions formantiques qui évoluent, ou des bruits étranges avec certaines caractéristiques de fréquence quand l’on dépasse r = 3.57.
J’ai utilisé l’équation différentielle pour contrôler les délais des grains avec le logiciel GiST, et j’ai obtenu des résultats remarquables pour effectuer des transitions du champ du micro-temps (timbre) au champ du macro-temps (rythme). On pourrait aussi utiliser l’équation pour la durée des grains. Imaginons une durée moyenne de grain au départ (disons, 40 msecs); on commence alors avec une durée plus ou moins constante, puis, à mesure que r augmente, on aura des doublements de période, les grains auront différentes durées fixes, et finalement, avec le chaos on aura une gamme de durées plus diverse. Il faut considérer que l’effet acoustique de cette équation va dépendre du contrôle des autres paramètres, car c’est l’ensemble des paramètres ainsi que leur interaction qui vont créer un résultat sonore final. Donc, on a beaucoup de possibilités d’affecter les différents paramètres de la synthèse granulaire formantique avec l’équation logistique, et même de combiner cette équation avec d’autres algorithmes de chaos, ou stochastiques.
b) L’équation du Gingerbread Man.
Barry Truax a utilisé l’équation du Gingerbread Man pour son application de synthèse granulaire en temps réel (Truax, 1988). Il exprime l’équation de la façon suivante:
x (n+1) = 1 - x (n-1) + /x( n)/
Truax utilise cette équation pour déterminer la fréquence des grains. L’équation peut être modifiée facilement par la mise en échelle de l’élément non-linéaire (la valeur absolue de x(n)) multipliée par un facteur r . Dans chaque cas on aura une nouvelle caractéristique de comportement chaotique, car la séquence résultante va dépendre des deux valeurs initiales qui peuvent être générées de façon aléatoire. Certaines valeurs vont produire une oscillation périodique, alors que d’autres vont produire des excursions chaotiques (Truax 1990).
Dans l’application de Truax, les deux valeurs initiales de x (n) et x (n-1) sont choisies de manière aléatoire chaque fois qu’on appuie sur le spacebar du clavier. On obtient la variation de l’équation avec l’inclusion du facteur r :
x(n+1) = 1 - x(n-1) + r . /x(n)/
Le facteur r met en échelle le facteur non-linéaire dans l’équation. Des petites valeurs de r vont générer des comportements lents et parfois périodiques et stables, pendant que des valeurs plus grandes vont augmenter la possibilité d’avoir un comportement chaotique.
Comme je l’ai déjà exprimé auparavant, cette équation pourrait aussi être utilisée pour contrôler les délais entre les grains, afin d’obtenir ainsi des comportements périodiques de délais qui vont produire des sons synchrones à caractère spectral, suivis de comportements chaotiques. L’idée de Truax de changer en temps réel les deux valeurs initiales ainsi que le facteur r pourrait être appliquée à d’autres systèmes de synthèse granulaire en temps réel tels que GiST.
c) La carte de Hénon.
La carte de Hénon constitue un modèle chaotique de dissipation et elle ne dérive d’aucun phénomène naturel. Cette carte générée par itération, s’exprime comme un système contenant deux équations différentielles:
xn+1 = yn + 1-Axn2, yn+1 + Bxn
où A et B sont des paramètres positifs constants, et où la séquence de valeurs de la sortie (x0, y0), (x1, y1),...(xn, yn) constitue des points dans le plan cartésien x y.
Le comportement de l’attracteur est déterminé par les valeurs assignées aux paramètres constants A et B; en général, les premiers 200 points ne sont pas utilisés, car ils appartient à la portion transitoire qui ne fait pas partie de l’attracteur. La durée de cette région transitoire va dépendre des conditions initiales et pourrait avoir parfois des centaines d’itérations pour certaines orbites. Le comportement du système de Hénon est contrôlé principalement par la variable A. Pour certaines valeurs de A au-dessous d’une certain valeur de transition (qui dépend cependant de la valeur de B), on aura des orbites périodiques. Pour les valeurs de A les plus basses, l’orbite se maintient dans le même point; la période commence à bondir lorsque la valeur de A augmente, et au-delà de la valeur de transition presque toutes les orbites deviennent chaotiques.
Bidlack (1992) a utilisé cet attracteur dans le macro-champ musical. Il utilise l’axe x pour déterminer la fréquence des notes dans une portée de quatre octaves, tandis qu’il laisse l’interprétation des points de l’axe y ouverte, celle-ci pouvant servir pour déterminer le rythme, la dynamique, ou le changement de timbre.
Les différents comportements de la carte de Hénon produisent des motifs musicaux différents; les attracteurs périodiques par exemple, produisent des motifs qui oscillent de manière répétitive et ressemblent à certaines séquences minimalistes de musique contemporaine; les attracteurs chaotiques produisent des textures qui se répètent régulièrement, mais il y a un patron de variation dans cette régularité; finalement, les orbites les plus chaotiques produisent des séquences complexes qui pourraient paraître aléatoires mais dans lesquelles on observe une tendance des notes (dans l’axe x) à constituer des motifs, sans pourtant réussir à le faire.
Avec la carte de Hénon, on peut voir clairement qu’il y a des structures de divers degrés de complexité qui ont un sens musical. La transition entre ces différentes structures nous donne la possibilité de créer un discours musical évolutif. Badlick a choisi la fréquence, et en conséquence la mélodie comme facteur principal, mais on pourrait faire de même pour le rythme ou pour le changement de timbre, qui constituent deux paramètres tout aussi déterminants. Les structures de la carte de Hénon peuvent aussi être utilisées dans le micro-domaine, pour contrôler des oscillateurs, ou la synthèse granulaire par exemple (Truax, 1990). Le comportement de cette carte est très semblable à d’autres équations chaotiques itératives, comme l’équation logistique, mais ici les répétitions des motifs au-dessous de la région du chaos total varient davantage.
Pour la synthèse granulaire, on pourrait utiliser l’axe x et l’axe y pour déterminer les délais entre les grains et la fréquence des grains respectivement, et en même temps, on pourrait utiliser x pour la dynamique et y pour le changement de timbre des grains. Mais une fois de plus, cartographier les paramètres d’une façon aussi stricte, donne comme résultat un objet chaotique sonore intéressant qui cependant ne constitue pas de la musique en soi. Il faudra toujours effectuer des manipulations postérieures, et un travail assidu de sélection et de montage. Toutefois, même si la création d’un nuage granulaire est trop déterminée par l’équation de Hénon, le mixage entre les différents nuages assurera la flexibilité nécessaire pour arriver à une véritable création musicale.
2.- Les fractales.
"That wch is below is like that wch is above & that wch is above is like yt wch is below to do ye miracles of one only thing".
Traduction de Issac Newton de la tablette d’émeraude (1680).
Le principe d’auto-similarité, qui est défini par un objet, une figure, un nombre, une proportion, ou tout élément qui se répète dans différentes échelles, est utilisé depuis longtemps comme une notion capable d’établir un certain ordre dans la nature. Les artistes de cultures anciennes l’ont utilisé notamment pour créer des structures géométriques qui constituaient des motifs décoratifs; plus récemment, à la fin du dix-neuvième et au début du vingtième siècle, des mathématiciens se sont intéressés aux qualités logarithmiques et exponentielles du principe d’auto-similarité, et ils ont construit des objets géométriques en s’en servant (Figure 8 ). Finalement, dans les années soixante-dix, le mathématicien Benoît Mandelbrot a étudié la caractéristique de dimensions fractionnaires de ce principe, et il a découvert que celui-ci était utile pour mesurer les qualités de certains objets qui ne pouvaient avoir de définition claire, c’est-à-dire, pour mesurer le degré de rugosité et d’irrégularité d’un objet (Gleick, 1987). Mandelbrot a alors constaté que le degré d’irrégularité trouvé dans différents éléments de la nature (comme par exemple les côtes maritimes) restait constant sur les différentes échelles, et ceci malgré l’existence apparente d’un élément Random absolu. Donc, Mandelbrot a trouvé un certain ordre dans la complexité de ces objets auto-similaires, et il les a nommés objets fractaux (Mandelbrot, 1983).

Figure 9.- Le Cantor Set. Construction fractale où l’on commence avec une ligne;on enlève la troisième partie du milieu; puis on enlève la troisième partie dessegments qui restent; et ainsi de suite. Les points qui demeurent sont nommé poussière de Cantor. Mandelbrot a considéré le Cantor Set comme un modèle de l’apparition d’erreurs dans une ligne de transmission électronique.
La notion fractale est fondamentale pour la musique. Dans le contrepoint du XII siècle, le même motif mélodique a été souvent utilisé à différentes vitesses (il a été contracté ou dilaté) (Risset, 1989); d’autre part, beaucoup de compositeurs de différentes époques ont crée des œuvres entières en partant d’un seul élément musical (mélodique ou rythmique principalement); en outre, des structures fractales plus strictes ont été trouvées dans la musique du Gamelan d’Indonésie, où le tempo des différents instruments est basé en séries exponentielles (2, 4, 8, 16) et la mélodie nucléaire est jouée par tous les instruments à différentes vitesses en même temps (Little, 1993). Si le principe fractal est capable de donner une certaine homogénéité sur toutes les différentes échelles, le domaine sonore peut à ce moment-là bénéficier également de cette qualité, et on peut l’utiliser alors aussi bien dans le micro-champ que dans le macro-champ sonore; en fait, ma proposition tout au long de ce travail, d’unir ces deux aspects musicaux, s’est affirmé en un certain sens sur les lois de ce principe fractal.
L’application de l’auto-similarité pour le contrôle de la synthèse granulaire est fort intéressante, particulièrement si on veut moduler du micro-domaine du timbre au macro-domaine de la mélodie et du rythme. Dans le logiciel de synthèse granulaire formantique GiST (Eckel et Rocha Iturbide, 1995), on a développé un algorithme de contrôle pour le délais de grains nommé geometime. (voir quatrième chapitre). Cet algorithme utilise le principe d’auto-similarité, car on multiplie un nombre (ou facteur) par une valeur de délai fixe, puis on multiplie le résultat par le même facteur, ensuite le nouveau résultat par le même facteur et ainsi de suite pendant un nombre défini d’entrées. Si on a un facteur de 1.3, et un délai de 20 msecs, on commence avec notre valeur de délai initial (20 msecs), ensuite, on multiplie la valeur du délai initial (20 msecs) par 1.5 (20 msecs * 1.5 = 26 msecs), puis ce résultat est multiplié encore par 1.5 (30 msecs * 1.5 = 33.8 msecs); le résultat est multiplié encore par 1.5 (33.8 msecs * 1.5 = 43.94 msecs), et ainsi de suite. Si on a 5 entrées, on aura les valeurs de délais suivantes: 20, 26, 33.8, 43.94, et 57.122; ces valeurs vont donner lieu aux sons granulaires manifestés dans le domaine du timbre, mais si on a davantage d’entrées, on aura à chaque fois de plus longs délais, et on entrera ainsi dans le domaine du macro-rythme. Le contrôle goemtime pourrait aussi être utilisé pour les fréquences de grains; dans ce cas on aura des nuages granulaires harmoniques si on multiplie par un facteur de nombre entier (1, 2, 3, 4). Par exemple, si on a 2 comme facteur et 50 Hz comme valeur initiale, on aura les fréquences suivantes: 50, 100, 200, 400, 800, 1600, etc, c’est-à-dire, seulement des octaves, mais si on a comme facteur un nombre décimal tel que 1.3, alors on aura des sons complètement inharmoniques.
D’autres chercheurs ont appliqué des structures fractales à la synthèse granulaire. Chapman, Clarke, Smith et Archbold (1996) ont utilisé l’équation de Mandelbrot (Mandelbrot Set) pour générer la distribution des grains. Ici la manière d’associer les points de la carte aux grains est semblable au procédé effectué avec les cartes non-linéaires itératives. Le principe fractal a également été appliqué dans d’autres domaines de la synthèse sonore depuis longtemps; Horacio Vaggione l’a utilisé dans sa composition Fractals pour saxophone et bande, où il a appliqué la même enveloppe d’amplitude dans différentes échelles temporelles; Jean-Claude Risset a aussi utilisé le principe fractal pour sa composition Little Boy (1968), où il a comprimé et dilaté la même enveloppe de fréquence dans le temps, pour créer des textures inharmoniques auto-similaires (Risset, 1989). Dans une autre composition (Mutations, 1969) il a utilisé la synthèse harmonique pour générer des accords fractals; un klang constitue un accord d’un certain nombre de tons (disons 4), avec des rapports spécifiques de fréquence entre eux; un klang d’un klang constitue la somme de 4 klangs avec ce même rapport de fréquences entre eux, et on peut continuer et construire des klangs de klangs de klangs, et ainsi de suite. D’autre part, David Yadegari (1991) a construit un logiciel de synthèse qui fonctionne de manière hiérarchique et récursive dans le domaine temporel, avec lequel il a réalisé des expériences sonores pour essayer de voir s’il était possible d’établir un rapport structurel entre le niveau normal de perception et la forme du signal auditif; il a conclu que la hiérarchie temporelle est une des hiérarchies de notre perception, et que les sons produits manifestaient la même structure dans les différentes couches de notre perception (Yadegari, 1991).
Le problème avec l’auto-similarité quand elle est exprimée de manière exponentielle est que les valeurs augmentent chaque fois plus vite et que si l’on ne commence avec des petits valeurs, on aura bientôt des valeurs trop grandes qui ne seront plus perceptibles (comme dans le cas de la fréquence). Avec les délais, le phénomène est un peu différent: si on a des valeurs trop grandes, on aura des espaces de temps trop grands et peu homogènes entre les grains; nous serons tout à fait capables de percevoir les grains ou notes, mais il n’y aura pas un rapport direct entre eux. Dans le sens inverse, si on va dans la direction du micro, on aura des discontinuités drastiques qui vont générer du bruit (Yadegary, 1991); d’ailleurs, ce doit être un bruit semblable à celui produit par le Cantor Set, qui est caractéristique dans les transmissions électroniques.
Nous avons vu qu’il y a différentes façons d’interpréter le principe fractal, et on pourrait conclure qu’il vaut mieux être flexible et subjectif plutôt que d’imiter une structure fractale point par point, car ceci constituerait simplement un jeu intéressant mais pas de l’art (Risset, 1989). Il est préférable de faire quelque chose de non strictement fractal, mais qui soit musical. Pour ma composition Transiciones de Fase pour tuba, trombone, cor, trompette et ordinateur, j’ai créé une structure fractale sur tous les niveaux temporels avec la répétition du ratio 3:2 dans différentes échelles, en commençant par les sections, puis avec les phrases, ensuite avec les motifs, et finalement avec la durée des notes (voir fin du dernier chapitre). Je ne suis pas absolument sûr s’il s’agissait d’une structure fractale juste, mais elle a bien fonctionné du point de vue musical.
Pour conclure avec cette section, il faut prendre en considération l’aspect psychoacoustique, car une structure fractale agit d’une façon dans le macro-domaine, mais elle agit différemment dans le micro-domaine. Il n’est peut-être pas possible de distinguer la structure fractale quand elle devient timbre sonore, car par exemple le rapport entre les grains dans l’échelle micro n’a rien à avoir avec leur rapport dans l’échelle macro (du point de vue perceptif). Dans le champ visuel on est peut-être certain que cela fonctionne si on dispose d’un microscope pour zoomer dans l’image, mais ce type de microscope n’existe pas dans la dimension temporelle, sauf si on se sert d’une analyse spectrale, laquelle n’a rien à voir avec notre perception. En tout cas, le principe d’auto-similarité a été et sera toujours efficace pour la création artistique, car malgré sa simplicité il est capable de créer des formes organiques et complexes très diverses.
IV.- Contrôle par automates cellulaires.
La nature offre beaucoup d’exemples de systèmes complexes contenant un grand nombre d’éléments dont le comportement est difficile à analyser. Des exemples étonnants d’auto-organisation montrent par exemple comment les entités individuelles d’une colonie de milliers de fourmis s’organisent sans l’aide d’un superviseur central, et ceci grâce à la communication entre voisins. Dans le milieu de l’informatique, les chercheurs ont essayé de créer des algorithmes qui fonctionnent avec cette philosophie; certains ont établit par exemple des processus de calcul où de simples agents interagissent de manière locale et évoluent dans le temps en parallèle; d’autres ont développé neural networks, des systèmes où un grand nombre d’éléments sont reliés et évoluent dans le temps par un ajustement de la force de leurs connections mutuelles. Tous ces méthodes informatiques constituent des systèmes dynamiques complexes et ils présentent les caractéristiques suivantes (Baylis, 1989):
-Ils ont un grand nombre d’éléments simples.
-Tous les éléments évoluent en parallèle dans le temps.
-La même règle externe est appliquée à tous les éléments.
-Les éléments réalisent seulement des interactions locales.
-Le système montre des propriétés globales émergentes.
Ces caractéristiques nous font automatiquement penser aux nuages granulaires, puisque ceux-ci constituent des ensembles sonores conformés par des milliers d’éléments simples, où leur mouvement est souvent établi par l’application de la même règle externe, et où tous les éléments évoluent ensemble dans le temps.
Un des systèmes dynamiques complexes qui présente les caractéristiques qu’on vient de décrire, et qui s’est beaucoup développé ces dernières années, est celui des automates cellulaires (AC). Ce système a été conçu à l’origine par Konrad Zuse et Stanislaw Ulam, et il a été appliqué par John von Neumman pour simuler le comportement des structures spatiales prolongées (Toffoli, Margolus, 1987). Le but principal de Neumman a été de créer un modèle biologique d’auto-reproduction pour savoir si une machine était capable de se reproduire automatiquement en produisant une copie identique d’elle-même.
Un automate cellulaire (d’une dimension) consiste en un rang de cellules, où chacune d’elles contient quelques nombres de base et une série de règles spécifiant comment ces nombres vont changer à chaque pas d’une l’horloge imaginaire. Supposons que dans l’état initial d’un automate, toutes les cellules soient remplies de 0’s, à l’exception d’une seule cellule occupée par un 1: ....01000000...., et supposons que les règles établies expriment que le nombre de chaque cellule doit être remplacé par la somme de soi-même plus son voisin de gauche. Donc, après un pas de l’horloge, l’automate aura le suivant état: ....01100000.... , et le pas d’horloge suivante, il y aura le suivant état: ....01210000.... , suivi de: ....01331000.... , ....01464100.... , et ainsi de suite.
Puisque les automates cellulaires typiques utilisent une application répétitive des règles fixées, on a comme résultat des motifs d’auto-similarité avec des structures complexes de type fractal. Une autre caractéristique intéressante des AC est qu’ils représentent des modèles d’évolution et de croissance. Les AC peuvent exister en une, deux, ou plusieurs dimensions. Un AC de deux dimensions est utilisé, par exemple, pour calculer l’écoulement d’un fluide ou le mouvement et la vitesse du gaz.
Vu les caractéristiques essentielles des automates cellulaires, il est clair que ceux-ci s’adaptent très bien à une conception quantique et discrète du son, et par conséquence, qu’ils pourraient être très utiles pour effectuer le contrôle des particules sonores. Ces dernières années, beaucoup de chercheurs d’informatique musicale se sont intéressés aux AC, et ils ont réalisé diverses applications de synthèse granulaire. Un de premiers à le faire a été probablement Peter Bowcott (1989), qui a utilisé le game of life de Conway (1968).
Le game of life est l’automate à deux dimensions le plus connu; ce jeu montre comment de simples règles qui opèrent à un niveau microscopique peuvent créer un comportement global compliqué des éléments. Dans ce jeu, les carrés d’une trame bi-dimensionnelle contiennent des cellules dont les états sont influencés par les états des cellules voisines. Le temps est discret, et d’une tranche de temps à l’autre chaque cellule est vive ou morte par l’effet des règles (Figure 10). Un des avantages d’un automate de ce type est que la quantité de data nécessaire est petite. On doit définir la configuration initiale, le temps du début, la durée de l’évolution, et l’association entre les coordonnées bi-dimensionelles des cellules et les paramètres de la synthèse granulaire choisis. J’ai signalé tout au long de ce chapitre, que tracer les points d’une carte visuelle dans le domaine de l’audio n’est pas une tâche simple si l’on veut avoir un résultat musical intéressant. Dans ce cas en particulier, si l’on tient compte des cellules vives dans une tranche de temps donné, on peut dire que la coordonnée x représente la fréquence tandis que la coordonnée y représente l’amplitude. Bowcott a remarqué l’incroyable ressemblance du game of life avec le système de trames de Xenakis (1971); il a suggéré d’interpréter chaque cellule vive comme un espace qui contient des grains distribués de manière aléatoire. Il estime que même si cette façon d’interpréter la transposition de l’automate ne reflète pas les data originaux, ce qui importe définitivement est le résultat musical final, plutôt qu’une tentative de reproduire la représentation visuelle de la sortie de l’automate dans le domaine de l’audio. Je suis complètement d’accord avec lui, et je crois que l’erreur principale de beaucoup de chercheurs-musiciens au moment d’effectuer l’association entre les data des algorithmes et les paramètres du domaine auditif - autant dans la synthèse sonore que dans la musique algorithmique en général - a été de se borner strictement à l’algorithme pour essayer de reproduire le processus dans le champ auditif, de manière directe et sans interprétation.

Figure 10.- Évolution de l’automate cellulaire de Bowcott (Bowcott, 1989).
Bowcott a développé davantage son système de synthèse granulaire (1990), mais il a modifié la méthode de contrôle en utilisant un algorithme de modélisation de population. Ici il s’est centré sur la variation de timbre des grains, un élément souvent oublié par les chercheurs. Les règles de ce système sont très intéressantes: un grain FM peut évoluer; à chaque génération il peut donner lieu à un ou à deux grains; si un seul grain est généré, il hérite toutes les caractéristiques de son parent et il émigre dans une aire harmonique favorable, mais si deux grains sont générés, alors ils ont tous deux des variations différentes de l’index de modulation de leur parent. L’environnement peut supporter un nombre spécifique de grains, mais il va favoriser ceux qui habitent dans une aire harmonique spécifique. Ce qui est intéressant dans ce système est que le compositeur peut varier le paramètre de l’environnement dans le processus évolutif, et qu’on peut même introduire d’autres variables, tels qu’un virus pour affecter le taux de croissance de la population. Dans cette exemple on peut voir qu’on a davantage de variables et par conséquent, davantage de contrôle pour affecter l’évolution des sons granulaires, par rapport à l’utilisation de l’algorithme game of life. Néanmoins, avec ce dernier algorithme on pourrait aussi appliquer le changement de timbre en modifiant le taux de modulation avec l’affectation des cellules qui se trouvent soit dans l’axe x soit dans l’axe y, mais le résultat sera plus déterministe car il dépendra strictement des conditions initiales et des règles du mécanisme du jeu. Toutefois, on pourrait toujours changer les règles et introduire de nouvelles conditions initiales au cours de l’évolution de l’AC (Millen, D. 1990).
Miranda a utilisé un automate cellulaire nommé Chemical Oscillator (ChaOs) pour créer une application de synthèse granulaire synchrone (Miranda, 1992, 1995). Cet algorithme simule un phénomène neurophysiologique connu sous le nom de neural reverbatory circuit . Avec le AC ChaOs, la valeur des cellules est représentée par un nombre situé entre 0 et n-1. La valeur 0 représente un état passif, tandis que la valeur n-1 représente un état brûlé . Toutes les valeurs entre 0 et n-1 présentent un degré de dépolarisation, et la proximité de toute valeur à n-1 augmente sa dépolarisation. Les règles de cet AC sont les suivantes:
a.- Si une cellule est passive elle peut ou non se dépolariser dans le pas suivant de l’horloge. Ceci dépend du nombre de cellules polarisées dans le voisinage (8 voisins), du nombre de cellules brûlées dans le voisinage, et de leur résistance à la dépolarisation.
b.- Si une cellule est dépolarisée, elle aura tendance à se dépolariser davantage avec la progression de l’horloge. Ceci dépend de la capacité k de la cellule et de la polarisation dans le voisinage. Le degré de polarisation dans le voisinage est la somme des nombres qui correspondent aux états de 8 voisins, divisé par le nombre des voisins polarisés.
c.- Si une cellule est brûlée, ChaOs génère une nouvelle cellule passive dans le prochain pas de l’horloge.
Chaque particule sonore créé par l’application de synthèse granulaire synchrone de Miranda est composée de plusieurs partiels, et chaque partiel est formé d’une onde sinus produite par un oscillateur. ChaOs va contrôler les valeurs de fréquence et de la durée de la particule. Les valeurs des cellules sont associées aux valeurs des fréquences, et un oscillateur est associé à un nombre déterminé de cellules. Les valeurs de la fréquence des partiels à chaque pas de l’horloge, sont déterminés par le ratio arithmétique des fréquences associées avec les valeurs des cellules qui appartiennent à un oscillateur. La durée totale d’un son est déterminée par le nombre d’itérations du AC et par la durée des particules (200 itérations de particules de 20 msecs vont donner comme résultat un son de 4 secondes).
La caractéristique principale de cet AC par rapport au timbre obtenu, est que les fréquences des partiels sont distribuées au début sur une large portée, et ensuite cette distribution tend à se stabiliser sur un cycle oscillatoire. Cet effet et ressemble à celui du ton d’un instrument où l’attaque constitue une variation des partiels dans une large porté, tandis que le corps du ton constitue la stabilisation et la périodicité des partiels (Miranda, 1995). Toutefois, les sons produits par ChaOs se rapprochent plutôt de ceux de l’eau qui coule. On peut varier la vitesse du pas de l’horloge, et de cette manière avoir des variations sur l’effet aquatique des sons.
L’idée de Miranda d’effectuer la synthèse granulaire synchrone est intéressante, ainsi que celle de manipuler le côté spectral des grains. Paradoxalement, le résultat est restreint aux sons aquatiques typiques de la synthèse granulaire asynchrone qui utilise des grains synthétiques. Dans ce sens, l’outil de synthèse de Miranda me paraît limité. D’autre part, la complexité du fonctionnement de l’AC ChaOs ne se reflète pas sur le résultat sonore, et le contrôle des paramètres est assez limité. Une fois de plus, le danger d’utiliser ce genre de processus dynamiques automatiques complexes, pour le contrôle de la synthèse, est que nous tendons à limiter le contrôle sur eux, et qu’à la fin, ils deviennent plus importants que nous, qui devenons des êtres passifs se contentant d’observer le résultat. Toutefois, avec une interprétation flexible on peut faire une bonne utilisation des AC pour contrôler la synthèse granulaire et avoir divers résultats sonores. Le principal avantage des AC est qu’ils peuvent produire en même temps des motifs périodiques et non périodiques complexes. Ceci permet d’utiliser des data pour déterminer par exemple les délais entre les grains, et d’avoir ainsi en même temps des sons à caractère spectral, et des sons plus rugueux ou rythmiques. Le désavantage est que l’évolution des cellules est rarement prévisible à partir des conditions initiales (Millen, 1990), et donc, que notre résultat sera toujours un peu aléatoire. En ce sens-là, certains algorithmes de chaos peuvent être plus utiles si l’on veut avoir un contrôle plus fin, car on connaît avec plus de certitude le type d’évolution qu’on aura.
V.- Contrôle hybride.
On ne doit pas être confiné à effectuer le contrôle de la synthèse granulaire avec un seul type de stratégie algorithmique; ceci constituerait un acte de puritanisme absurde dont le seul résultat serait de limiter le pouvoir de notre imagination pour combiner les différentes méthodes de contrôle qu’on connaît.
Les méthodes hybrides de contrôle - qui consistent à mixer différentes stratégies algorithmiques - sont bien efficaces pour résoudre des problèmes esthétiques issus de besoins musicaux spécifiques. Il est vrai qu’utiliser un seul algorithme de contrôle pourrait être convenable, surtout car l’on a un principe unique qui va donner une certain homogénéité au résultat sonore. Toutefois, nous nous trouvons très souvent dans une impasse, car certains aspects de l’algorithme employé nous intéressent, mais d’autres ne nous intéressent pas; il faut à ce moment-là abandonner notre austérité rigoriste et commencer à faire de la "nouvelle cuisine, en additionnant à notre recette originale des ingrédients et des épices d’autres cuisines. Pour donner un exemple, dans la section précédente on a décrit comment le chercheur Peter Bowcott a employé l’automate cellulaire game of life pour effectuer le contrôle de particules sonores; au lieu de se borner à une transposition directe entre cellules et grains (où chaque cellule serait équivalente à un grain), il a décidé que ceci ne donnerait pas un résultat musical intéressant; il a donc interprété chaque cellule comme une série de grains, et les grains de chaque cellule ont été contrôlés par une méthode stochastique, complètement différente de celle des automates cellulaires (Bowcott, 1989).
1.- L’emploi des méthodes symboliques en combinaison avec d’autres algorithmes.
Au début de cet chapitre on a établi la différence entre les stratégies "symboliques" basées sur la connaissance (knowledge-based) pour la solution de problèmes donnés, et les stratégies "sub-symboliques" (subsymbolic methodes), qui utilisent des représentations analogiques conservant implicitement ce qu’elles reproduisent dans leur représentation (Beyls, 1991). Les méthodes symboliques telles que les systèmes basés sur règles (rule-based systems) et la programmation orientée par objets, sont rarement employées pour la synthèse granulaire, car ce sont des stratégies qui servent à l’affectation d’éléments qualitatifs plutôt que quantitatifs. Toutefois, il serait toujours possible de considérer l’emploi des stratégies symboliques en combinaison avec des stratégies sub-symboliques, et avec des méthodes stochastiques.
La philosophie de la programmation orientée par objets pourrait s’adapter à un système hybride de contrôle granulaire. Selon cette philosophie, un simple objet est capable de réaliser des tâches complexes, et l’on peut ensuite unir plusieurs de ces objets pour conformer une entité plus grande et indépendante qui pourrait être en même temps contrôlée par un autre objet, et cet objet pourrait en même temps être contrôlé par d’autres structures d’objets (Figure 11). On peut continuer ainsi, et conformer un système hiérarchique qui s’adapte bien aux besoins d’une architecture musicale cohérente (Hiller, 1981). Dans la synthèse granulaire, l’élément le plus petit est un grain, mais un grain seul ne veut rien dire. L’objet le plus simple constituerait en conséquence un ensemble de grains, et la structure de cet objet devrait forcément être de type aléatoire, stochastique, ou sub-symbolique. Ensuite, on pourrait avoir plusieurs voix granulaires avec des caractéristiques différentes, et la participation et la modification de ces voix dans le temps pourraient être réglées par des objets appartenant à une hiérarchie plus élevée. Les voix pourraient être aussi interdépendantes, c’est-à-dire, que certaines caractéristiques des voix capables d’être mesurées pourraient affecter d’autres voix. Par exemple, on pourrait dire que si la densité d’une certaine voix dépasse 500 grains par seconde, une autre voix est déclenchée, ou que si les valeurs de l’index de modulation des grains des différentes voix se trouvent toutes dans une portée spécifique, elles deviendront stables pendant une certaine période de temps.
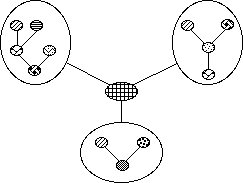
Figure 11.- Un système hiérarchique de programmation orienté par objets.
Une autre manière de combiner des stratégies symboliques avec des stratégies stochastiques et sub-symboliques pour le contrôle des grains, est d’utiliser chaque groupe pour un domaine temporel différent (Eckel et Rocha Iturbide, 1995). L’idée serait ici d’établir un seul environnement dans lequel il soit possible d’effectuer le micro-contrôle des grains (niveau de DSP) et le macro-contrôle des grains et de structures granulaires pré-définies (niveau de composition musical global) (Eckel et Arroyo, 1994). Dans la synthèse granulaire il nous faut des méthodes de contrôle capables de gérer le destin de milliers de grains; on doit donc utiliser des méthodes stochastiques et sub-symboliques dans ce niveau, mais si on réalise des processus qui vont du micro-domaine au macro-domaine, les petits grains deviendront des notes, et on pourrait à partir de ce moment changer de stratégie et contrôler chaque note avec une grammaire générative basée sur règles. Une autre possibilité de combiner les deux domaines dans le même niveau temporel est la suivante: on peut établir que chaque fois qu’un certain nombre de grains d’un micro-processus dépasse une certaine valeur de durée (70 msecs par exemple), et qu’en même temps les valeurs de délai entre les grains sont au-delà d’un certain seuil (100 msecs par exemple), on considérera chaque grain comme une note (le micro-processus devient un macro-processus); certaines règles établiront ensuite que selon la fréquence de la note il y aura des déclenchements de nouveaux micro-processus dans le macro-processus (Figure 12). La globalité des micro et des macro-processus constituerait une composition musicale.
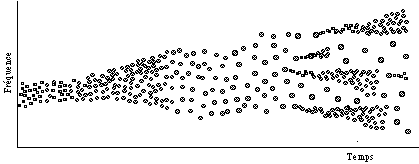
Figure 12.- Interaction entre divers micro et macro-processus granulaires dans le même niveau temporel. La globalité de tous ces processus constituerait une composition musicale.
La philosophie hiérarchique pour le contrôle des grains a été contemplée aussi dans le contexte de la synthèse granulaire par analyse-synthèse. Nunn, Purvis, et Manning (1996) ont généré des structures de quanta de haut niveau et sur différentes échelles. Les quanta sont d’abord conformés en atomes qui ont des caractéristiques différentes (il y a 16 différents atomes en tout). Puis, un groupe d’atomes constitue une molécule. Finalement, une interface graphique permet la manipulation des molécules (21 maximum) pour effectuer des opérations linéaires (multiplication, convolution) et non linéaires (dilatation temporelle, transposition).
2.- D’autres combinaisons d’algorithmes.
Au sein du logiciel GiST pour la synthèse granulaire formantique (Eckel et Rocha Iturbide, 1995), qui a d’ailleurs été programmé avec le langage orienté par objets MAX (Puckette, 1991), on a combiné des algorithmes stochastiques avec des algorithmes sub-symboliques, et même avec un algorithme plus proche des structures musicales utilisées dans le macro-domaine, qui pourrait être considéré comme un algorithme symbolique (cet algorithme est geomtime).
On a d’abord combiné deux différents algorithmes stochastiques, un tendency mask stochastique avec une valeur minimale et une valeur maximale (nommé randist) qui génère des valeurs aléatoires entre les deux valeurs, et un facteur brownien qui détermine la continuité ou discontinuité des valeurs aléatoires. De plus, on peut avoir différentes distributions de probabilité des valeurs aléatoires (voir logiciel GiST dans le quatrième chapitre). D’autre part, l’algorithme de chaos (l’équation logistique de May) est combiné avec le tendency mask randist mais aussi avec la possibilité d’avoir un facteur brownien; de plus, on a un contrôle qui détermine le fonctionnement de l’équation de chaos; si cette valeur est égale à un, l’équation fonctionne à 100%, si la valeur est égale à 0.5, l’équation fonctionne à 50%, et si la valeur est égale à 0, l’équation ne fonctionne pas.
On a développé un autre algorithme qui pourrait être considéré comme symbolique. Geomtime consiste en une combinaison de délais issus de la multiplication géométrique d’un facteur avec une valeur de délai. Les valeurs de délai résultantes sont ensuite choisies de façon aléatoire, mais il y a un algorithme (geomtime filter) qui détermine combien de ces délais seront choisis, et un autre algorithme qui détermine la fréquence de changement entre chaque délai (un facteur 100 effectue un changement constant de délais, un facteur 50 effectue un changement de délais seulement la moitié du temps). De plus, on peut combiner geomtime avec le tendency mask randist, et avec le facteur brownien.
Avec cette gamme de possibilités de combinaison des paramètres algorithmiques, on peut obtenir des résultats sonores très divers. De plus, avec Geomtime il est possible d’avoir un contrôle des délais plutôt indéterministe ou plutôt déterministe. Cet algorithme a l’avantage de pouvoir créer des textures rythmiques reconnaissables qui peuvent agir autant dans le micro-domaine du timbre, pour la création des textures sonores, que dans le macro-domaine des notes (quand la durée des grains et les délais deviennent assez longs), pour créer des motifs rythmiques musicaux.
Il serait intéressant d’avoir plusieurs processus granulaires en parallèle, chacun géré par un contrôle algorithmique différent. Malheureusement, on n’a pas pu développer cette modalité à cause d’une limitation de l’ordinateur et de la carte DSP pour effectuer le calcul. Il serait également possible d’avoir un contrôle différent pour chaque paramètre de la synthèse; on pourrait par exemple contrôler les fréquences avec l’algorithme chaotique, les délais avec l’algorithme stochastique, la durée des grains avec l’algorithme de temps géométrique, etc. Ceci n’a pas été envisagé, mais on pourrait l’appliquer dans une future version. Je pense qu’il y aurait un sens musical si on employait le geomtime pour les délais, et par exemple, l’algorithme de chaos pour les fréquences.
3.- Rétro-action hybride.
On pourrait combiner différents algorithmes dans un contexte automatique (auto-génération), et avoir un système hiérarchique avec différents niveaux de contrôle. Par exemple, si on utilise un algorithme de chaos tel que l’équation logistique pour générer les fréquences des grains, il nous faut déterminer la valeur initiale de croissance x , et le taux de changement r. Ces deux valeurs pourraient être déterminées de manière stochastique, mais on pourrait aussi utiliser une autre équation de chaos, une équation des automates cellulaires, ou même un système par règles pour les produire. Les méthodes sub-symboliques telles que les équations de chaos et les automates cellulaires à deux dimensions, possèdent deux variables, un axe x et un axe y. Chaque axe pourrait alors servir à interpréter chacune des variables de l’équation logistique. On pourrait avoir en même temps un autre couple d’algorithmes pour contrôler les délais, un autre pour le timbre des grains, et ainsi de suite.